逆運動学を使用した 2 次元パスのトレース

はじめに

この例では、inverseKinematicsクラスを使用して単純な 2 次元マニピュレーターの逆運動学を計算する方法を示します。マニピュレーターロボットは、回転ジョイントをもつ単純な 2 自由度の平面マニピュレーターで、剛体を rigidBodyTreeオブジェクトに組み立てて作成されています。円形の軌跡が 2 次元平面に作成され、逆運動学ソルバーに点として渡されます。ソルバーは必要なジョイント位置を計算してこの軌跡を得ます。最後に、ロボットがアニメーション化されて、円形の軌跡を達成するロボットコンフィギュレーションが示されます。

ロボットの構築

rigidBodyTree オブジェクトと剛体を、関連付けられたジョイントと共に作成します。各剛体の幾何学的特性を指定し、ロボットに追加します。

空の剛体ツリーモデルで始めます。

robot = rigidBodyTree('DataFormat','column','MaxNumBodies',3);

ロボットアームのアーム長さを指定します。

L1 = 0.3;
L2 = 0.3;

'joint1' ジョイントをもつ 'link1' ボディを追加します。

body = rigidBody('link1');
joint = rigidBodyJoint('joint1', 'revolute');
setFixedTransform(joint,trvec2tform([0 0 0]));
joint.JointAxis = [0 0 1];
body.Joint = joint;
addBody(robot, body, 'base');

'joint2' ジョイントをもつ 'link2' ボディを追加します。

body = rigidBody('link2');
joint = rigidBodyJoint('joint2','revolute');
setFixedTransform(joint, trvec2tform([L1,0,0]));
joint.JointAxis = [0 0 1];
body.Joint = joint;
addBody(robot, body, 'link1');

固定ジョイント 'fix1' をもつエンドエフェクタ 'tool' を追加します。

body = rigidBody('tool');
joint = rigidBodyJoint('fix1','fixed');
setFixedTransform(joint, trvec2tform([L2, 0, 0]));
body.Joint = joint;
addBody(robot, body, 'link2');

ロボットの詳細を表示して、入力プロパティを検証します。ロボットには、リンクボディが回転ジョイントを介して親ボディに接続されている 2 つの非固定ジョイントが存在する必要があり、エンドエフェクタは固定ジョイントを介して親ボディに接続されています。

showdetails(robot)

--------------------
Robot: (3 bodies)

 Idx    Body Name    Joint Name    Joint Type    Parent Name(Idx)   Children Name(s)
 ---    ---------    ----------    ----------    ----------------   ----------------
   1        link1        joint1      revolute             base(0)   link2(2)  
   2        link2        joint2      revolute            link1(1)   tool(3)  
   3         tool          fix1         fixed            link2(2)   
--------------------

軌跡の定義

10 秒間にわたってトレースされる円を定義します。この円は、半径 0.15 で xy 平面にあります。

t = (0:0.2:10)'; % Time
count = length(t);
center = [0.3 0.1 0];
radius = 0.15;
theta = t*(2*pi/t(end));
points = center + radius*[cos(theta) sin(theta) zeros(size(theta))];

逆運動学の解

inverseKinematics オブジェクトを使用して、軌跡に沿って指定されたエンドエフェクタ位置を達成するロボットコンフィギュレーションの解を求めます。

コンフィギュレーションの解を行列 qs として事前に割り当てます。

q0 = homeConfiguration(robot);
ndof = length(q0);
qs = zeros(count, ndof);

逆運動学ソルバーを作成します。このワークフローのエンドエフェクタ姿勢における唯一の重要な係数は xy 直交座標の点であるため、weight ベクトルの第 4 要素と第 5 要素にはゼロでない重みを指定します。その他すべての要素はゼロに設定します。

ik = inverseKinematics('RigidBodyTree', robot);
weights = [0, 0, 0, 1, 1, 0];
endEffector = 'tool';

点の軌跡をループして円をトレースします。それぞれの点に対して ik オブジェクトを呼び出して、エンドエフェクタ位置を達成するジョイントコンフィギュレーションを生成します。後で使用するためにコンフィギュレーションを保存します。

qInitial = q0; % Use home configuration as the initial guess
for i = 1:count
    % Solve for the configuration satisfying the desired end effector
    % position
    point = points(i,:);
    qSol = ik(endEffector,trvec2tform(point),weights,qInitial);
    % Store the configuration
    qs(i,:) = qSol;
    % Start from prior solution
    qInitial = qSol;
end

解のアニメーション化

この特定のロボットコンフィギュレーションを使用して、解の各座標系についてロボットをプロットします。また、目的の軌跡をプロットします。

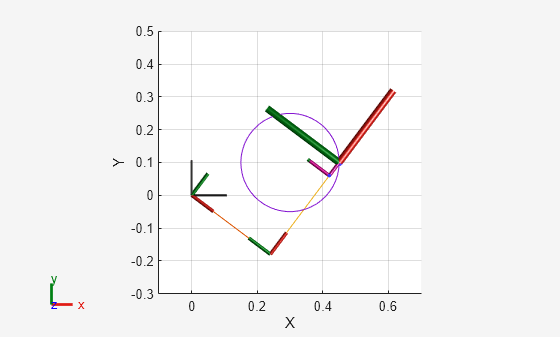
軌跡の最初のコンフィギュレーションにロボットを表示します。プロットを調整して、円が描画されている 2 次元平面を表示します。目的の軌跡をプロットします。

figure
show(robot,qs(1,:)');
view(2)
ax = gca;
ax.Projection = 'orthographic';
hold on
plot(points(:,1),points(:,2),'k')
axis([-0.1 0.7 -0.3 0.5])

ロボットの軌跡を 1 秒あたり 15 フレームの固定レートで表示するように、rateControlオブジェクトを設定します。逆運動学ソルバーから、各コンフィギュレーションのロボットを表示します。表示された軌跡をアームがトレースする様子を観察します。

framesPerSecond = 15;
r = rateControl(framesPerSecond);
for i = 1:count
    show(robot,qs(i,:)','PreservePlot',false);
    drawnow
    waitfor(r);
end

参考

rigidBodyTree | rigidBody | rigidBodyJoint | inverseKinematics