rfbudget
Create RF budget object and compute RF budget results for chain of 2-port elements
Description
Use the rfbudget object to create an RF budget object and
compute the RF budget results for a chain of 2-port elements. In this RF chain, you can
use a 2-port element such as amplifier,
nport, or
modulator. You
can also open the rfbudget object in an RF
Budget Analyzer app and then export the completed circuit to RF Blockset™ for circuit envelope analysis.
The rfbudget object assumes a reference temperature of 290 K when
calculating the SNR of an RF chain.
Creation
Syntax
Description
rfobj = rfbudget creates an rfbudget
object, rfobj, with default empty property values.
rfobj = rfbudget(
sets Elements, InputFrequency, AvailableInputPower, and SignalBandwidth properties and computes the RF budget
analysis. By default, if any of the input properties are changed, the object
recomputes results.elements,inputfreq,inputpwr,bandwidth)
rfobj = rfbudget(___,
sets the AutoUpdate property. You can use this syntax with any of the
previous syntaxes.autoupdate)
rfobj = rfbudget(Name=value) sets Properties using one
or more name-value arguments. You can specify multiple name-value
arguments.
Properties
RF budget elements, specified as an RF budget object or an array of RF budget objects. Use an array of RF budget objects when you perform RF budget analysis on an RF chain.
This table lists supported RF budget elements you can use to design an RF chain.
| Element Type | RF Budget Elements |
|---|---|
| Linear Elements | attenuator |
rfantenna | |
rffilter | |
nport | |
seriesRLC | |
shuntRLC | |
phaseshift | |
txlineCoaxial | |
txlineCPW | |
txlineMicrostrip | |
txlineParallelPlate | |
txlineRLCGLine | |
txlineStripline | |
txlineTwoWire | |
txlineEquationBased | |
txlineDelayLossless | |
txlineDelayLossy | |
| Nonlinear Elements | amplifier |
modulator | |
rfelement | |
mixerIMT |
Example: a = amplifier; m = modulator; rfbudget(Elements=[a
m]) calculates the RF budget analysis of the amplifier and
modulator circuit.
Input frequency of the signal, specified as a nonnegative scalar or column vector (since R2023a) of size M-by-1 in Hz. M represents number of frequencies. If the input frequency is a vector, then the RF budget object analyzes each input frequency separately.
Example: InputFrequency=2e9
Data Types: double
Power applied at the input of the cascade, specified as a scalar in dBm.
Example: AvailableInputPower=-30
Data Types: double
Signal bandwidth at the input of the cascade, specified as a scalar in Hz.
Example: SignalBandwidth=10
Data Types: double
Automatically recompute the RF budget analysis by incorporating changes
made to the existing circuit, specified as true or
false.
Setting AutoUpdate to false turns
off automatic budget recomputation as parameters change. To compute the
budget result of an rfbudget object when you set the
AutoUpdate property to false,
use the computeBudget function.
Example: AutoUpdate=false
Data Types: logical
Computation method, specified as Friis or
HarmonicBalance. The Friis solver
is faster and the HarmonicBalance solver supports
computation of second-order nonlinearities such as OIP2.
When you set the Solver type to
HarmonicBalance, the tone and harmonic-dependent
properties are displayed.
Note
The HarmonicBalance solver does not support
architectures where the input or output frequencies at any stage in the
cascade are nonzero and less than SignalBandwidth.
Example: Solver='Friis'
Data Types: string
Since R2024a
Maximum number of harmonics to use for each tone in one- and two-tone
harmonic balance (HB) analyses, specified as a positive integer. Use this
property for faster HB analysis and set MaxHarmonics to
[] to return to the default automatic determination
of harmonics.
Example: MaxHarmonics=5
Dependencies
To enable this property, set Solver to HarmonicBalance.
Data Types: double
Since R2024a
Minimum number of harmonics to use for each tone in one- and two-tone
harmonic balance (HB) analyses, specified as a positive integer. Use this
property to achieve higher-fidelity HB simulation in highly nonlinear
systems and set MinHarmonics to []
to return to the default automatic determination of harmonics.
Example: MinHarmonics=5
Dependencies
To enable this property, set Solver to HarmonicBalance.
Data Types: double
Number of harmonics to use for one-tone harmonic balance (HB) analysis,
specified as a positive integer. For each two-tone analysis,
max(3,HarmonicOrder) harmonics is used. Use the
default value for automatic determination of harmonics.
Use this property to
Accelerate the HB analysis by reducing the number of harmonics needed for a mildly nonlinear system.
Ensure harmonic balance accuracy by increasing the number of harmonics used in a highly nonlinear system.
Dependencies
To enable this property, set Solver to HarmonicBalance.
Data Types: double
This property is read-only.
Output frequencies in Hz, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Data Types: double
This property is read-only.
Output power in dBm, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Data Types: double
This property is read-only.
Transducer power gains in dB, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Data Types: double
This property is read-only.
Noise figures in dB, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Note
If AvailableInputPower is very large, it can result in
negative NF values during harmonic balance analysis
[1].
Data Types: double
This property is read-only.
Input-referred second-order intercept (IIP2) in dBm, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Dependencies
To compute IIP2 values, set Solver to HarmonicBalance.
Data Types: double
This property is read-only.
Output-referred second-order intercept (OIP2) in dBm, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Dependencies
To compute OIP2 values, set Solver to HarmonicBalance.
Data Types: double
This property is read-only.
The Input-referred third-order intercept (IIP3) in dBm, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Data Types: double
This property is read-only.
The Output-referred third-order intercept (OIP3) in dBm, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Data Types: double
This property is read-only.
Signal-to-noise ratio (SNR) in dB, returned as one of the following:
Scalar when M and N =
1Vector when M or N =
1Matrix when M and N >
1
where M represents the number of frequencies in the input and N represents the number of stages in the cascade.
Data Types: double
Display a progress bar with a cancel button during harmonic balance
analysis, specified as true or
false.
Data Types: logical
Object Functions
show | Display RF budget object in RF Budget Analyzer app |
computeBudget | Compute results of RF budget object |
computeAMPMTable | Compute AM/AM-AM/PM table representation from RF budget object |
exportScript | Export MATLAB code that generates RF budget object |
exportRFBlockset | Export RF budget object to RF Blockset Model |
exportTestbench | Export RF budget object to RF Blockset measurement testbench model |
exportTransmitter | Export RF budget summary to create phased transmitter |
exportReceiver | Export RF budget summary to create phased receiver |
rfplot | Plot cumulative RF budget result vs. cascade input frequency and amplifier power characteristics |
smithplot | Plot measurement data on Smith chart |
polar | Plot specified object parameters on polar coordinates |
Examples
Open a default RF budget object.
obj = rfbudget
obj =
rfbudget with properties:
Elements: []
InputFrequency: [] Hz
AvailableInputPower: [] dBm
SignalBandwidth: [] Hz
Solver: Friis
AutoUpdate: true
Create an amplifier with a gain of 4 dB.
a = amplifier(Gain=4);
Create a modulator with an OIP3 of 13 dBm.
m = modulator(OIP3=13);
Create an N-port element using passive.s2p.
n = nport('passive.s2p');Create an RF element with a gain of 10 dB.
r = rfelement(Gain=10);
Calculate the RF budget of a series of RF elements at an input frequency of 2.1 GHz, an available input power of –30 dBm, and a bandwidth of 10 MHz.
b = rfbudget([a m r n],2.1e9,-30,10e6)
b =
rfbudget with properties:
Elements: [1x4 rf.internal.rfbudget.Element]
InputFrequency: 2.1 GHz
AvailableInputPower: -30 dBm
SignalBandwidth: 10 MHz
Solver: Friis
AutoUpdate: true
Analysis Results
OutputFrequency: (GHz) [ 2.1 3.1 3.1 3.1]
OutputPower: (dBm) [ -26 -26 -16 -20.6]
TransducerGain: (dB) [ 4 4 14 9.4]
NF: (dB) [ 0 0 0 0.1392]
IIP2: (dBm) []
OIP2: (dBm) []
IIP3: (dBm) [ Inf 9 9 9]
OIP3: (dBm) [ Inf 13 23 18.4]
SNR: (dB) [73.98 73.98 73.98 73.84]
Type the show command at the command window to display the analysis in the RF Budget Analyzer app.
show(b)

Create an RF system.
Create an RF bandpass filter using the Touchstone® file RFBudget_RF.
f1 = nport('RFBudget_RF.s2p','RFBandpassFilter');
Create an amplifier with a gain of 11.53 dB, a noise figure (NF) of 1.53 dB, and an output third-order intercept (OIP3) of 35 dBm.
a1 = amplifier(Name='RFAmplifier',Gain=11.53,NF=1.53,OIP3=35);Create a demodulator with a gain of –6 dB, a NF of 4 dB, and an OIP3 of 50 dBm.
d = modulator(Name='Demodulator',Gain=-6,NF=4,OIP3=50, ... LO=2.03e9,ConverterType='Down');
Create an IF bandpass filter using the Touchstone file RFBudget_IF.
f2 = nport('RFBudget_IF.s2p','IFBandpassFilter');
Create an amplifier with a gain of 30 dB, a NF of 8 dB, and an OIP3 of 37 dBm.
a2 = amplifier(Name='IFAmplifier',Gain=30,NF=8,OIP3=37);Calculate the RF budget of the system using an input frequency of 2.1 GHz, an input power of –30 dBm, and a bandwidth of 45 MHz.
b = rfbudget([f1 a1 d f2 a2],2.1e9,-30,45e6)
b =
rfbudget with properties:
Elements: [1x5 rf.internal.rfbudget.Element]
InputFrequency: 2.1 GHz
AvailableInputPower: -30 dBm
SignalBandwidth: 45 MHz
Solver: Friis
AutoUpdate: true
Analysis Results
OutputFrequency: (GHz) [ 2.1 2.1 0.07 0.07 0.07]
OutputPower: (dBm) [-31.53 -20 -26 -27.15 2.847]
TransducerGain: (dB) [-1.534 9.996 3.996 2.847 32.85]
NF: (dB) [ 1.533 3.064 3.377 3.611 7.036]
IIP2: (dBm) []
OIP2: (dBm) []
IIP3: (dBm) [ Inf 25 24.97 24.97 4.116]
OIP3: (dBm) [ Inf 35 28.97 27.82 36.96]
SNR: (dB) [ 65.91 64.38 64.07 63.83 60.41]
Plot the available output power.
rfplot(b,'Pout')
view(90,0)
Plot the transducer gain.
rfplot(b,'GainT')
view(90,0)
Plot S-parameters of an RF system on a Smith Chart and a Polar plot.
s = smithplot(b,1,1,'GridType','ZY');

p = polar(b,2,1);

Create two modulators with output-referred second-order intercept set to 20 and available power gain set to 3.
m = modulator(Gain=3,OIP2=20,ImageReject=false,ChannelSelect=false); m2 = modulator(Gain=3,OIP2=20,ImageReject=false,ChannelSelect=false);
Create an RF budget object specifying the input frequency of the signal, power applied at cascade, and signal bandwidth. Select HarmonicBalance as solver method to compute nonlinear effects such as IIP2 and OIP2.
b = rfbudget([m m2],2.1e9,-30,100e6,Solver='HarmonicBalance')b =
rfbudget with properties:
Elements: [1x2 modulator]
InputFrequency: 2.1 GHz
AvailableInputPower: -30 dBm
SignalBandwidth: 100 MHz
Solver: HarmonicBalance
WaitBar: true
AutoUpdate: true
Analysis Results
OutputFrequency: (GHz) [ 3.1 4.1]
OutputPower: (dBm) [ -27 -24]
TransducerGain: (dB) [ 3 6]
NF: (dB) [ 3.01 7.783]
IIP2: (dBm) [ 17 4.457]
OIP2: (dBm) [ 20 10.46]
IIP3: (dBm) [ Inf Inf]
OIP3: (dBm) [ Inf Inf]
SNR: (dB) [60.96 56.19]
Create an amplifier with a gain of 10 dB.
a = amplifier(Gain=10);
Create a modulator with an OIP3 of 13 dBm.
m = modulator(OIP3=13);
Create an N-port circuit element using passive.s2p.
n = nport('passive.s2p');Calculate the RF budget of a series of RF elements at an input frequency of 2.1 GHz, an available input power of –30 dBm, and a bandwidth of 10 MHz using HB analysis. Set the number of harmonics that the rfbudget object should use for all the tones in HB analyses.
b = rfbudget([a m n],2.1e9,-30,10e6,... Solver="HarmonicBalance",HarmonicOrder=3)
b =
rfbudget with properties:
Elements: [1x3 rf.internal.rfbudget.Element]
InputFrequency: 2.1 GHz
AvailableInputPower: -30 dBm
SignalBandwidth: 10 MHz
Solver: HarmonicBalance
HarmonicOrder: 3
WaitBar: true
AutoUpdate: true
Analysis Results
OutputFrequency: (GHz) [ 2.1 3.1 3.1]
OutputPower: (dBm) [ -20 -20 -24.6]
TransducerGain: (dB) [ 10 9.996 5.396]
NF: (dB) [-2.842e-14 -0.004353 0.3376]
IIP2: (dBm) [ Inf Inf Inf]
OIP2: (dBm) [ Inf Inf Inf]
IIP3: (dBm) [ Inf 2.997 2.998]
OIP3: (dBm) [ Inf 12.99 8.391]
SNR: (dB) [ 73.98 73.98 73.64]
Create an RF bandpass filter using the Touchstone® file RFBudget_RF.
f1 = nport('RFBudget_RF.s2p','RFBandpassFilter');
Create an amplifier with a gain of 11.53 dB, a noise figure (NF) of 1.53 dB, and an output third-order intercept (OIP3) of 35 dBm.
a1 = amplifier(Name='RFAmplifier',Gain=11.53,NF=1.53,OIP3=35);Create a demodulator with a gain of –6 dB, a NF of 4 dB, and an OIP3 of 50 dBm.
d = modulator(Name='Demodulator',Gain=-6,NF=4,OIP3=50, ... LO=2.03e9,ConverterType='Down');
Create an IF bandpass filter using the Touchstone file RFBudget_IF.
f2 = nport('RFBudget_IF.s2p','IFBandpassFilter');
Create an amplifier with a gain of 30 dB, a NF of 8 dB, and an OIP3 of 37 dBm.
a2 = amplifier(Name='IFAmplifier',Gain=30,NF=8,OIP3=37);Calculate the RF budget of the system using an input frequency of 2.1 GHz, an input power of –30 dBm, and a bandwidth of 45 MHz.
b = rfbudget([f1 a1 d f2 a2],2.1e9,-30,45e6);
Show the analysis in the RF plot.
rfplot(b)

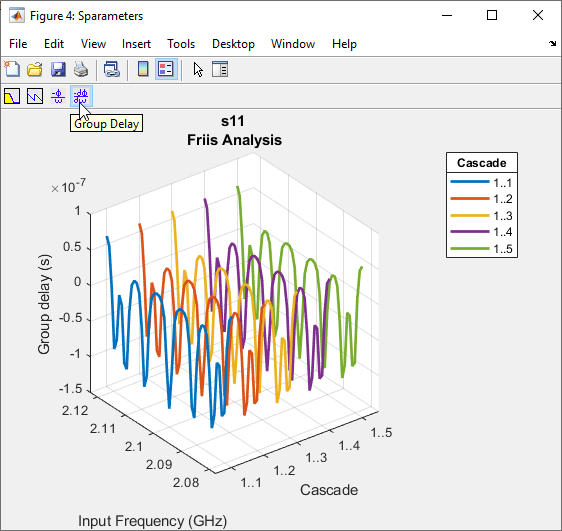
Group Delay
To plot the group delay, first plot the S11 data for the RF System.
rfplot(b,1,1)

Use the Group Delay option on the plot graph to plot the group delay of the RF system.
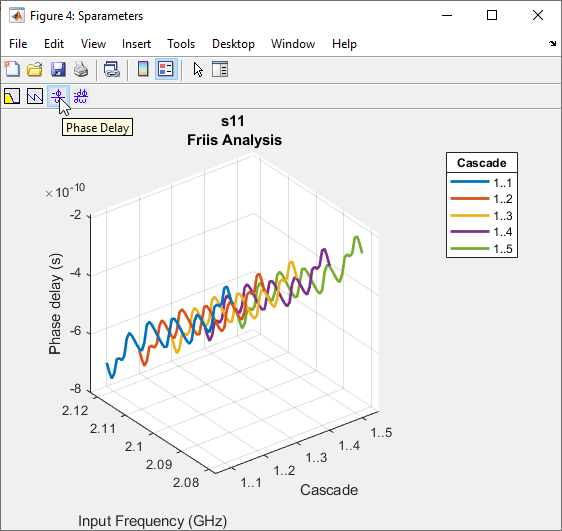
Phase Delay
Use the Phase Delay option on the plot graph to plot the phase delay of the RF System.
Tips
The Touchstone file in the
nportobject must be passive at all specified frequencies. To make N-port S-parameters passive, use themakepassivefunction.
Algorithms
ABCD parameters are used in the computation of S-parameters of the cascade for Friis Solver. When S21 = 0, conversion to ABCD results in NaNs. For such cases, modifications to the S-parameters are made as follows:
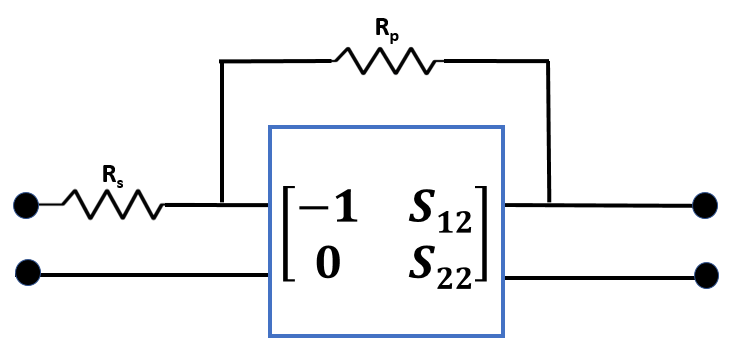
Connected large resistance (Rp = 1012 ohm) in parallel with the network.
Connected small resistance (Rs = 10-12 ohm) in series to the beginning of the network.
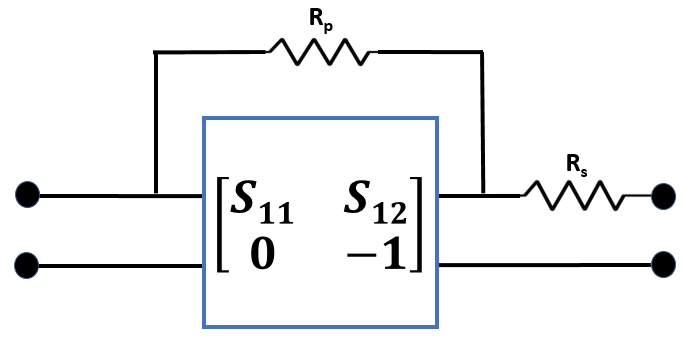
Connected large resistance (Rp = 1012 ohm) in parallel with the network.
Connected small resistance (Rs = 10-12 ohm) in series after the network.
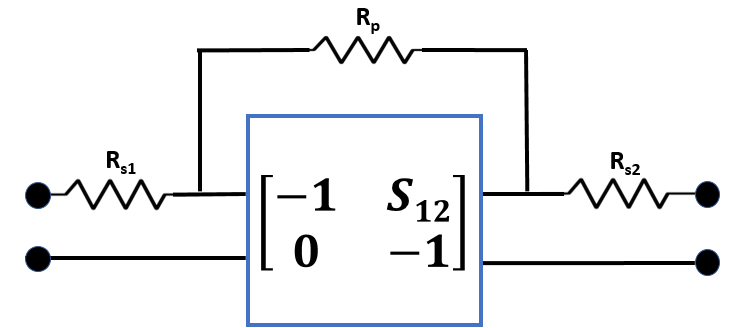
Connected large resistance (Rp = 1012 ohm) in parallel with the network.
Connected small resistance (Rs = 10-12 ohm) in series to the beginning of the network.
Connected small resistance (Rs = 10-12 ohm) in series after the network.

Connected large resistance (Rp = 1012 ohm) in parallel with the network.
References
[1] Roychowdhury, J., D. Long, and P. Feldmann. “Cyclostationary Noise Analysis of Large RF Circuits with Multitone Excitations.” IEEE Journal of Solid-State Circuits 33, no. 3 (March 1998): 324–36. https://doi.org/10.1109/4.661198.
Version History
Introduced in R2017aYou can now use the rfbudget object to increase the number of
harmonics for higher fidelity HB simulation and reduce the number of harmonics for
faster HB simulation.
rfbudget is
recommend over rfckt.cascade and analyze
because it enables you to:
Create an RF budget chain and compute the RF budget results for a chain of two-port elements. You can include linear and nonlinear elements in your chain. For more information, see Elements.
Compute gain, noise figure, IP2, and IP3 of cascaded RF elements using Friis and harmonic balance solvers and export the RF chain to RF Blockset and
rfsystemfor circuit envelope analysis.
Starting this release, you can specify the InputFrequency
property of the rfbudget
object as a nonnegative scalar or as a column vector of nonnegative values.
The rfbudget object throws an error if you set the
InputFrequency property to a negative value. Update the
property to a positive value in existing circuits designed using the
rfbudget object to ensure accurate RF budget computations.
Specify the number of harmonics for all tones in HB analyses by setting the
HarmonicOrder property in the rfbudget object.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)