MDP 環境での強化学習エージェントの学習

この例では、一般的なマルコフ決定過程 (MDP) 環境を解決するために Q 学習エージェントに学習させる方法を示します。これらのエージェントの詳細については、Q 学習エージェントを参照してください。

MDP 環境は次のようなグラフです。

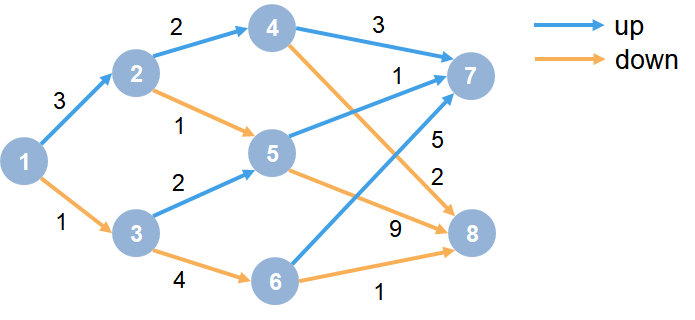
ここで、以下となります。

各円は状態を表します。
各状態において、上がる (up) または下がる (down) の判定があります。
エージェントは状態 1 から開始します。
エージェントは、グラフ内の各遷移の値に等しい報酬を受け取ります。
学習の目標は、最大の累積報酬を収集することです。

再現性のための乱数ストリームの固定

サンプルコードには、さまざまな段階で乱数の計算が含まれる場合があります。サンプルコード内のさまざまなセクションの先頭にある乱数ストリームを固定すると、実行するたびにセクション内の乱数シーケンスが維持されるため、結果が再現される可能性が高くなります。詳細については、Results Reproducibilityを参照してください。シード 0 で乱数ストリームを固定し、メルセンヌ・ツイスター乱数アルゴリズムを使用します。乱数生成に使用されるシード制御の詳細については、rngを参照してください。

previousRngState = rng(0,"twister");

出力 previousRngState は、ストリームの前の状態に関する情報が格納された構造体です。例の最後で、状態を復元します。

MDP 環境の作成

8 つの状態と 2 つのアクション ("up" と "down") をもつ MDP モデルを作成します。

MDP = createMDP(8,["up";"down"]);

上のグラフからの遷移をモデル化するには、MDP の状態遷移行列と報酬行列を変更します。既定では、これらの行列にはゼロが格納されています。MDP モデルと MDP オブジェクトのプロパティの作成の詳細については、createMDPを参照してください。

MDP の状態遷移行列と報酬行列を指定します。たとえば、以下のコマンドのようにします。

最初の 2 行は、アクション 1 ("up") を実行することによる状態 1 から状態 2 への遷移と、この遷移に対する +3 の報酬を指定する。
次の 2 行は、アクション 2 ("down") を実行することによる状態 1 から状態 3 への遷移と、この遷移に対する +1 の報酬を指定する。

MDP.T(1,2,1) = 1;
MDP.R(1,2,1) = 3;
MDP.T(1,3,2) = 1;
MDP.R(1,3,2) = 1;

同様に、グラフ内の残りのルールの状態遷移と報酬を指定します。

% State 2 transition and reward
MDP.T(2,4,1) = 1;
MDP.R(2,4,1) = 2;
MDP.T(2,5,2) = 1;
MDP.R(2,5,2) = 1;
% State 3 transition and reward
MDP.T(3,5,1) = 1;
MDP.R(3,5,1) = 2;
MDP.T(3,6,2) = 1;
MDP.R(3,6,2) = 4;
% State 4 transition and reward
MDP.T(4,7,1) = 1;
MDP.R(4,7,1) = 3;
MDP.T(4,8,2) = 1;
MDP.R(4,8,2) = 2;
% State 5 transition and reward
MDP.T(5,7,1) = 1;
MDP.R(5,7,1) = 1;
MDP.T(5,8,2) = 1;
MDP.R(5,8,2) = 9;
% State 6 transition and reward
MDP.T(6,7,1) = 1;
MDP.R(6,7,1) = 5;
MDP.T(6,8,2) = 1;
MDP.R(6,8,2) = 1;
% State 7 transition and reward
MDP.T(7,7,1) = 1;
MDP.R(7,7,1) = 0;
MDP.T(7,7,2) = 1;
MDP.R(7,7,2) = 0;
% State 8 transition and reward
MDP.T(8,8,1) = 1;
MDP.R(8,8,1) = 0;
MDP.T(8,8,2) = 1;
MDP.R(8,8,2) = 0;

MDP の終了状態として状態 "s7" と状態 "s8" を指定します。

MDP.TerminalStates = ["s7";"s8"];

このプロセスモデルの強化学習 MDP 環境を作成します。

env = rlMDPEnv(MDP);

エージェントの初期状態が常に状態 1 になるように指定するには、エージェントの初期状態を返すリセット関数を指定します。この関数は、各学習エピソードとシミュレーションの開始時に呼び出されます。初期状態を 1 に設定する無名関数ハンドルを作成します。

env.ResetFcn = @() 1;

Q 学習エージェントの作成

Q 学習エージェントを作成するには、まず MDP 環境からの観測仕様とアクション仕様を使用して Q テーブルモデルを作成します。テーブルモデルの学習率を 0.1 に設定します。

obsInfo = getObservationInfo(env);
actInfo = getActionInfo(env);
qTable = rlTable(obsInfo, actInfo);

次に、テーブルモデルから Q 値クリティック関数を作成します。

qFunction = rlQValueFunction(qTable, obsInfo, actInfo);

最後に、このクリティック関数を使用して Q 学習エージェントを作成します。この学習では、次のようにします。

割引されていない長期報酬に有利となるように、割引率 1.0 を指定。
エージェントの ε-greedy 探索モデルの初期イプシロン値 0.9 を指定。
減衰率を 1e-3 に指定し、イプシロンパラメーターの最小値を 0.1 に指定。探索を徐々に減衰させることで、エージェントは学習の後半の段階に向けて貪欲方策を活用できるようになります。
モーメンタム項付き確率的勾配降下法 (SGDM) アルゴリズムを使用して、学習率 0.1 でテーブルモデルを更新。
L2 正則化係数 0 を使用。この例では、正則化を無効にすることが、割引されていない長期報酬の推定の精度を上げるのに役立ちます。

agentOpts = rlQAgentOptions;
agentOpts.DiscountFactor = 1;
agentOpts.EpsilonGreedyExploration.Epsilon = 0.9;
agentOpts.EpsilonGreedyExploration.EpsilonDecay = 1e-3;
agentOpts.EpsilonGreedyExploration.EpsilonMin = 0.1;
agentOpts.CriticOptimizerOptions = rlOptimizerOptions( ...
    Algorithm="sgdm", ...
    LearnRate=0.1, ...
    L2RegularizationFactor=0);
qAgent = rlQAgent(qFunction,agentOpts);

Q 学習エージェントの作成の詳細については、rlQAgentおよびrlQAgentOptionsを参照してください。

Q 学習エージェントの学習

エージェントに学習させるには、まず、学習オプションを指定します。この例では、次のオプションを使用します。

400 個のエピソードについて学習 (各エピソードは最大 50 タイムステップ持続)。
エピソード報酬を平均化するためのウィンドウ長を 30 に指定。

学習オプションの詳細については、rlTrainingOptionsを参照してください。

trainOpts = rlTrainingOptions;
trainOpts.MaxStepsPerEpisode = 50;
trainOpts.MaxEpisodes = 400;
trainOpts.ScoreAveragingWindowLength = 30;
trainOpts.StopTrainingCriteria = "none";

再現性のために乱数ストリームを固定します。

rng(0,"twister");

関数 train を使用して、エージェントに学習させます。これは、完了するまで数分かかる場合があります。この例の実行時間を節約するために、doTraining を false に設定して事前学習済みのエージェントを読み込みます。エージェントに学習させるには、doTraining を true に設定します。

doTraining = false;
if doTraining
    % Train the agent.
    trainingStats = train(qAgent,env,trainOpts); %#ok<UNRCH>
else
    % Load pretrained agent for the example.
    load("genericMDPQAgent.mat","qAgent"); 
end

Q 学習の結果の検証

再現性のために乱数ストリームを固定します。

rng(0,"twister");

学習結果を検証するには、関数simを使用して、学習環境でエージェントをシミュレーションします。エージェントが最適なパスを見つけることに成功し、累積報酬は 13 になります。

Data = sim(qAgent,env);
cumulativeReward = sum(Data.Reward)

cumulativeReward = 
13

割引係数が 1 に設定されているため、学習済みエージェントの Q テーブルの値は、環境の割引されていない収益と一致します。

QTable = getLearnableParameters(getCritic(qAgent));
QTable{1}

ans = 8×2 single matrix

   13.0000   12.0000
    5.0000   10.0000
   11.0000    9.0000
    3.0000    2.0000
    1.0000    9.0000
    5.0000    1.0000
         0         0
         0         0

TrueTableValues = [13,12;5,10;11,9;3,2;1,9;5,1;0,0;0,0]

TrueTableValues = 8×2

    13    12
     5    10
    11     9
     3     2
     1     9
     5     1
     0     0
     0     0