初期動作データからのバッテリーサイクル寿命の予測

ライブスクリプトを開く

この例では、線形回帰、教師ありの機械学習アルゴリズムを使用して、高速充電リチウムイオンバッテリーの残りのサイクル寿命を予測する方法を説明します。物理学に基づいたモデル化手法を使用したリチウムイオンバッテリーのサイクル寿命の予測は、動作状態が多岐にわたり、製造元が同じバッテリーでもデバイスの変動性が大きいため、非常に複雑です。このシナリオでは、十分なテストデータが使用可能であれば、機械学習に基づく手法により有望な結果が示されます。バッテリーの寿命の早い段階でバッテリーのサイクル寿命を正確に予測できれば、新しい製造プロセスを迅速に検証できるようになります。また、エンドユーザーは性能劣化を特定し、十分な時間的余裕をもって故障したバッテリーを交換できるようになります。そのために、残りのサイクル寿命の予測では最初の 100 サイクルに基づく特徴のみが考慮され、予測誤差は約 10% であることが示されています [1]。

データセット

データセットには、充電と放電のさまざまなプロファイル下で定格容量が 1.1 Ah、定格電圧が 3.3 V の、リチウムイオン電池 124 個の測定値が含まれています。データセット全体にはこちら [2] から、詳細説明にはこちら [1] からアクセスできます。この例でデータは、抽出される特徴に関連する測定値のサブセットのみが含まれるようキュレートされています。これにより、考慮対象の機械学習モデルの性能を変更せずにダウンロードのサイズが削減されます。学習データには 41 個の電池の測定値、検証データには 43 個の電池の測定値、テストデータには 40 個の電池の測定値が含まれます。各電池のデータは構造体に格納され、次の情報が含まれています。

説明的なデータ: 電池のバーコード、充電に関するポリシー、サイクル寿命
サイクルごとの概要データ: サイクル番号、放電容量、内部抵抗、充電時間
サイクル内で収集されるデータ: 時刻、温度、線形内挿された放電容量、線形内挿された電圧

MathWorks サポートファイルサイトからデータ (これは、約 1.7 GB の大規模なデータセットです) を読み込みます。

url = 'https://ssd.mathworks.com/supportfiles/predmaint/batterycyclelifeprediction/v1/batteryDischargeData.zip';
websave('batteryDischargeData.zip',url);
unzip('batteryDischargeData.zip')
load('batteryDischargeData');

特徴抽出

放電容量はバッテリーの健全性を反映し得る主要な特徴で、電気自動車では、その値は走行距離を示します。学習データにある電池の最初の 1,000 サイクルについて放電容量をプロットし、電池の寿命全体での変化を可視化します。

figure, hold on;
for i = 1:size(trainData,2)
    if numel(trainData(i).summary.cycle) == numel(unique(trainData(i).summary.cycle))
      plot(trainData(i).summary.cycle, trainData(i).summary.QDischarge);      
    end
end
ylim([0.85,1.1]),xlim([0,1000]);
ylabel('Discharge capacity (Ah)');
xlabel('cycle');

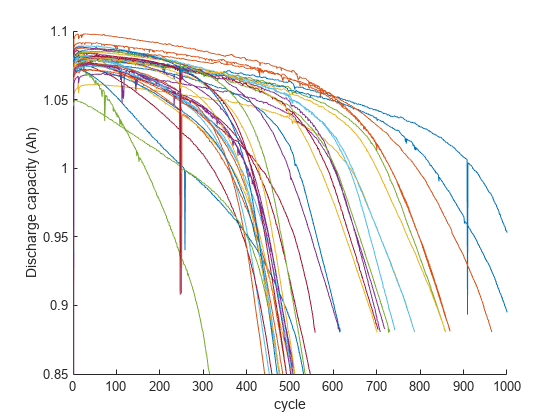
プロットでわかるように、容量劣化は寿命末期付近で加速します。一方で、最初の 100 サイクルで容量劣化はほとんどなく、これ自体はバッテリーのサイクル寿命の予測に適した特徴ではありません。そのため、残りのサイクル寿命の予測では、各サイクルの電圧曲線を電池の内部抵抗や温度などの追加の測定値と共に考慮する、データドリブンの手法が検討されます。特定サイクルにおける電圧の関数としての、放電電圧曲線 Q(V) のサイクルごとの変化は、重要な特徴空間です [1]。特に、サイクル間の放電電圧曲線の変化 $Δ Q (V)$ は、劣化診断において非常に効果的です。そのため、100 サイクル目と 10 サイクル目の間の電圧 $Δ Q_{100 - 10} (V)$ の関数として、放電容量の差を選択します。

figure, hold on;
for i = 1:size(testData,2)
    plot((testData(i).cycles(100).Qdlin - testData(i).cycles(10).Qdlin), testData(i).Vdlin)   
end
ylabel('Voltage (V)'); xlabel('Q_{100} - Q_{10} (Ah)');

各電池の $Δ Q_{100 - 10} (V)$ の曲線を状態インジケーターとして使用して、要約統計量を計算します。これらの要約統計量の物理的意味はあまり重要ではなく、ただ予測の力があることが示されればいいことに注意してください。たとえば、この両対数プロットで示されるとおり、 $Δ Q_{100 - 10} (V)$ の分散とサイクル寿命には高い相関性があり、この手法が適切であることが確認されます。

figure;
trainDataSize = size(trainData,2);
cycleLife = zeros(trainDataSize,1);
DeltaQ_var = zeros(trainDataSize,1);
for i = 1:trainDataSize
    cycleLife(i) = size(trainData(i).cycles,2) + 1;
    DeltaQ_var(i) = var(trainData(i).cycles(100).Qdlin - trainData(i).cycles(10).Qdlin);
end
loglog(DeltaQ_var,cycleLife, 'o')
ylabel('Cycle life'); xlabel('Var(Q_{100} - Q_{10}) (Ah^2)');

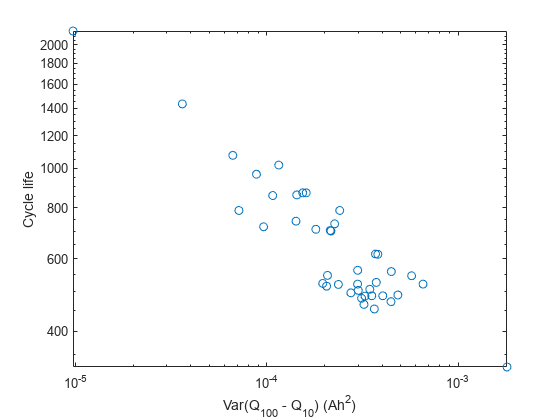
次に、生の測定データから以下の特徴 (大かっこ内が変数名) を抽出します [1]。

$Δ Q_{100 - 10} (V)$ の対数分散 [DeltaQ_var]
$Δ Q_{100 - 10} (V)$ の対数の最小値 [DeltaQ_min]
容量劣化曲線の線形近似の勾配、サイクル 2 ～ 100 [CapFadeCycle2Slope]
容量劣化曲線の線形近似の切片、サイクル 2 ～ 100 [CapFadeCycle2Intercept]
サイクル 2 での放電容量 [Qd2]
最初の 5 サイクルの平均充電時間 [AvgChargeTime]
最小内部抵抗、サイクル 2 ～ 100 [MinIR]
サイクル 2 と 100 の間の内部抵抗の差 [IRDiff2And100]

関数 helperGetFeatures は生の測定データを受け取り、上記の特徴を計算します。table に特徴が含まれる XTrain と、期待される残りのサイクル寿命が含まれる yTrain を返します。

[XTrain,yTrain] = helperGetFeatures(trainData);
head(XTrain)

ans=8×8 table
    DeltaQ_var    DeltaQ_min    CapFadeCycle2Slope    CapFadeCycle2Intercept     Qd2      AvgChargeTime     MinIR      IRDiff2And100
    __________    __________    __________________    ______________________    ______    _____________    ________    _____________

     -5.0839       -1.9638          6.4708e-06                1.0809            1.0753       13.409        0.016764     -3.3898e-05 
     -4.3754       -1.6928          1.6313e-05                1.0841            1.0797       12.025        0.016098      4.4186e-05 
     -4.1464       -1.5889          8.1708e-06                  1.08            1.0761       10.968        0.015923     -0.00012443 
     -3.8068       -1.4216          -8.491e-06                1.0974            1.0939       10.025        0.016083     -3.7309e-05 
     -4.1181       -1.6089          2.2859e-05                1.0589            1.0538       11.669        0.015963     -0.00030445 
     -4.0225       -1.5407          2.5969e-05                1.0664            1.0611       10.798        0.016543     -0.00024655 
     -3.9697       -1.5077          1.7886e-05                1.0762            1.0721       10.147        0.016238      2.2163e-05 
     -3.6195       -1.3383         -1.0356e-05                1.0889            1.0851       9.9247        0.016205     -6.6087e-05

モデルの開発: Elastic Net 正則化を使った線形回帰

正則化された線形モデルを使用して、電池の残りのサイクル寿命を予測します。線形モデルは低い計算コストで、高い解釈可能性を提供します。線形モデルの形式は次のとおりです。

$y_{i} = w^{T} x_{i} + β$

ここで、 $y_{i}$ は電池 $i$ のサイクル数、 $x_{i}$ は電池 $i$ の $p$ 次元特徴ベクトル、 $w$ は $p$ 次元のモデル係数ベクトル、 $β$ はスカラーの切片です。線形モデルは、特徴間の高い相関性に対処するために elastic net を使用して正則化されます。厳密に 0 と 1 の間にある $α$ 、および非負の正則化係数 $λ$ について、elastic net は次の問題を解きます。

$w_{}^{ˆ} = \min_{w} ‖ y - X w - β ‖_{2}^{2} + λ P_{α} (w)$

ここで、 $P_{α} (w) = \frac{(1 - α)}{2} ‖ w ‖_{2}^{2} + α ‖ w ‖_{1}$ です。Elastic net は、 $α$ が 0 に近いとリッジ回帰に近づき、 $α = 1$ のときに lasso 正規化と同じになります。学習データを使用してハイパーパラメーター $α$ および $λ$ が選択され、係数 $w$ の値が決定されます。関数 lasso は $α$ と $λ$ の各値について、当てはめられた最小二乗回帰係数と、モデルの当てはめに関する情報を出力として返します。関数 lasso は $λ$ パラメーターの値のベクトルを受け取ります。そのため、 $α$ の各値について、RMSE が最も低くなるモデル係数 $w$ および $λ$ が計算されます。[1] で提案されているとおり、交差検証でのモンテカルロの反復回数を 1 にして、4 分割交差検証を使用します。

rng("default")

alphaVec = 0.01:0.1:1;
lambdaVec = 0:0.01:1;
MCReps = 1;
cvFold = 4;

rmseList = zeros(length(alphaVec),1);
minLambdaMSE = zeros(length(alphaVec),1);
wModelList = cell(1,length(alphaVec));
betaVec = cell(1,length(alphaVec));

for i=1:length(alphaVec)
    [coefficients,fitInfo] = ...
        lasso(XTrain.Variables,yTrain,'Alpha',alphaVec(i),'CV',cvFold,'MCReps',MCReps,'Lambda',lambdaVec);
    wModelList{i} = coefficients(:,fitInfo.IndexMinMSE);
    betaVec{i} = fitInfo.Intercept(fitInfo.IndexMinMSE);       
    indexMinMSE = fitInfo.IndexMinMSE;
    rmseList(i) = sqrt(fitInfo.MSE(indexMinMSE));    
    minLambdaMSE(i) = fitInfo.LambdaMinMSE;    
end

当てはめたモデルをロバストにするには、検証データを使用してハイパーパラメーター $α$ および $λ$ の最終値を選択します。そのためには、学習データを使用して計算された 4 つの最も低い RMSE 値に対応する係数を選択します。

numVal = 4;
[out,idx] = sort(rmseList);
val = out(1:numVal);
index = idx(1:numVal);

alpha = alphaVec(index);
lambda = minLambdaMSE(index);
wModel = wModelList(index);
beta = betaVec(index);

係数の各セットについて、検証データにおける予測値と RMSE を計算します。

[XVal,yVal] = helperGetFeatures(valData);
rmseValModel = zeros(numVal);
for valList = 1:numVal   
   yPredVal = (XVal.Variables*wModel{valList} + beta{valList});
   rmseValModel(valList) = sqrt(mean((yPredVal-yVal).^2));
end

検証データを使用する際に、RMSE が最小のモデルを選択します。学習データにおいて RMSE 値が最小となるモデルが、検証データにおいて RMSE 値が最小となるモデルであるとは限りません。検証データを使用すると、それによってモデルのロバスト性が向上します。

[rmseMinVal,idx] = min(rmseValModel);
wModelFinal = wModel{idx};
betaFinal = beta{idx};

学習済みモデルの性能評価

テストデータには 40 個の電池に対応する測定値が含まれています。testData から特徴と、それに対応する応答を抽出します。学習済みモデルを使用して、testData における各電池の残りのサイクル寿命を予測します。

[XTest,yTest] = helperGetFeatures(testData);
yPredTest = (XTest.Variables*wModelFinal + betaFinal);

テストデータについて、予測されたサイクル寿命と実際のサイクル寿命の対比を可視化します。

figure;
scatter(yTest,yPredTest)
hold on;
refline(1, 0);
title('Predicted vs Actual Cycle Life')
ylabel('Predicted cycle life');
xlabel('Actual cycle life');

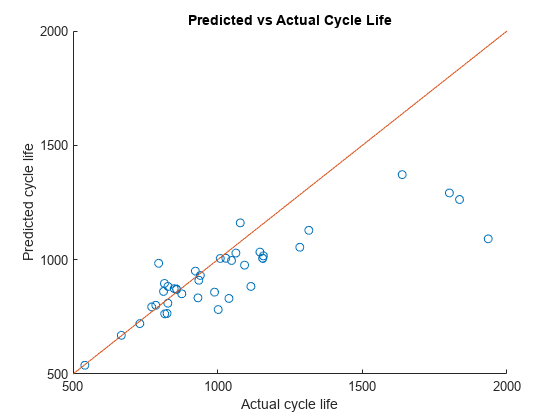
上記プロットのすべての点が斜めの線に近いのが理想的です。上記のプロットから、学習済みモデルは、残りのサイクル寿命が 500 から 1200 サイクルまでの間であるときに高い性能を示していることが分かります。1200 サイクルを超えると、モデルの性能は低下しています。この領域において、モデルは常に残りのサイクル寿命を低く見積もっています。これは主に、テストデータセットと検証データセットに総寿命が約 1000 サイクルの電池がかなり多く含まれているからです。

予測された残りのサイクル寿命の RMSE を計算します。

errTest = (yPredTest-yTest);
rmseTestModel = sqrt(mean(errTest.^2))

rmseTestModel = 211.6148

性能評価で考慮されるもう一つのメトリクスは平均誤差率で、次のように定義 [1] されます。

$% e r r = \frac{1}{n} Σ_{i = 1}^{n} \frac{| y_{i} - {y_{}^{ˆ}}_{i} |}{y_{i}} \times 100$

n = numel(yTest);
nr = abs(yTest - yPredTest);
errVal = (1/n)*sum(nr./yTest)*100

errVal = 9.9817

まとめ

この例では、最初の 100 サイクルのみの測定値を基に、elastic net で正則化された線形回帰モデルを使用してバッテリーのサイクル寿命を予測する方法を説明しました。生の測定値データからカスタム特徴を抽出し、学習データを使用して、elastic net で正則化された線形回帰モデルを当てはめました。次に、検証データセットを使用してハイパーパラメーターを選択しました。このモデルをテストデータに対して使用し、性能評価を行いました。最初の 100 サイクルのみの測定値を使用してテストデータセットに含まれる電池の残りのサイクル寿命を予測したところ、RMSE は 211.6、平均誤差率は 9.98% となりました。

参考文献

[1] Severson, K.A., Attia, P.M., Jin, N. et al. "Data-driven prediction of battery cycle life before capacity degradation." Nat Energy 4, 383–391 (2019). https://doi.org/10.1038/s41560-019-0356-8

[2] https://data.matr.io/1/

サポート関数

function [xTable, y] = helperGetFeatures(batch)
% HELPERGETFEATURES function accepts the raw measurement data and computes
% the following feature:
%
% Q_{100-10}(V) variance [DeltaQ_var]
% Q_{100-10}(V) minimum [DeltaQ_min]
% Slope of linear fit to the capacity fade curve cycles 2 to 100 [CapFadeCycle2Slope]
% Intercept of linear fit to capacity fade curve, cycles 2 to 100 [CapFadeCycle2Intercept]
% Discharge capacity at cycle 2 [Qd2]
% Average charge time over first 5 cycles [AvgChargeTime]
% Minimum Internal Resistance, cycles 2 to 100 [MinIR]
% Internal Resistance difference between cycles 2 and 100 [IRDiff2And100]

N = size(batch,2); % Number of batteries

% Preallocation of variables
y = zeros(N, 1);
DeltaQ_var = zeros(N,1);
DeltaQ_min = zeros(N,1);
CapFadeCycle2Slope = zeros(N,1);
CapFadeCycle2Intercept = zeros(N,1);
Qd2 = zeros(N,1);
AvgChargeTime = zeros(N,1);
IntegralTemp = zeros(N,1);
MinIR = zeros(N,1);
IRDiff2And100 = zeros(N,1);

for i = 1:N
    % cycle life
    y(i,1) = size(batch(i).cycles,2) + 1;
    
    % Identify cycles with time gaps
    numCycles = size(batch(i).cycles, 2);
    timeGapCycleIdx = [];
    jBadCycle = 0;
    for jCycle = 2: numCycles
        dt = diff(batch(i).cycles(jCycle).t);
        if max(dt) > 5*mean(dt)
            jBadCycle = jBadCycle + 1;
            timeGapCycleIdx(jBadCycle) = jCycle;
        end
    end
    
    % Remove cycles with time gaps
    batch(i).cycles(timeGapCycleIdx) = [];
    batch(i).summary.QDischarge(timeGapCycleIdx) = [];
    batch(i).summary.IR(timeGapCycleIdx) = [];
    batch(i).summary.chargetime(timeGapCycleIdx) = [];
    
    % compute Q_100_10 stats
    DeltaQ = batch(i).cycles(100).Qdlin - batch(i).cycles(10).Qdlin;
    DeltaQ_var(i) = log10(abs(var(DeltaQ)));
    DeltaQ_min(i) = log10(abs(min(DeltaQ)));
    
    % Slope and intercept of linear fit for capacity fade curve from cycle
    % 2 to cycle 100
    coeff2 = polyfit(batch(i).summary.cycle(2:100), batch(i).summary.QDischarge(2:100),1);
    CapFadeCycle2Slope(i) = coeff2(1);
    CapFadeCycle2Intercept(i) = coeff2(2);
    
    %  Discharge capacity at cycle 2
    Qd2(i) = batch(i).summary.QDischarge(2);
    
    % Avg charge time, first 5 cycles (2 to 6)
    AvgChargeTime(i) = mean(batch(i).summary.chargetime(2:6));
    
    % Integral of temperature from cycles 2 to 100
    tempIntT = 0;
    for jCycle = 2:100
        tempIntT = tempIntT + trapz(batch(i).cycles(jCycle).t, batch(i).cycles(jCycle).T);
    end
    IntegralTemp(i) = tempIntT;
    
    % Minimum internal resistance, cycles 2 to 100
    temp = batch(i).summary.IR(2:100);
    MinIR(i) = min(temp(temp~=0));
    IRDiff2And100(i) = batch(i).summary.IR(100) - batch(i).summary.IR(2);
end

xTable = table(DeltaQ_var, DeltaQ_min, ...
    CapFadeCycle2Slope, CapFadeCycle2Intercept,...
    Qd2, AvgChargeTime, MinIR, IRDiff2And100);

end

参考

lasso

初期動作データからのバッテリー サイクル寿命の予測