pagefun による GPU 上の小さな行列問題のパフォーマンス改善

マップの設定

多くの対象物が含まれた部屋の次元を定義します。

roomDimensions = [50 50 5];

この例の最後に示しているサポート関数 randomTransforms は、ランダムな値を用いて N 個の変換を初期化し、構造体を出力として提供します。位置と向きを、3 行 1 列のベクトル T と 3 行 3 列の回転行列 R を使用して表します。N 個の並進は 3 行 N 列の行列にパックされ、回転は 3×3×N の配列にパックされます。

関数 randomTransforms を使用して、1000 個の対象物のマップおよびロボットの開始位置を設定します。

numFeatures = 1000;
Map = randomTransforms(numFeatures,roomDimensions);
Robot = randomTransforms(1,roomDimensions);

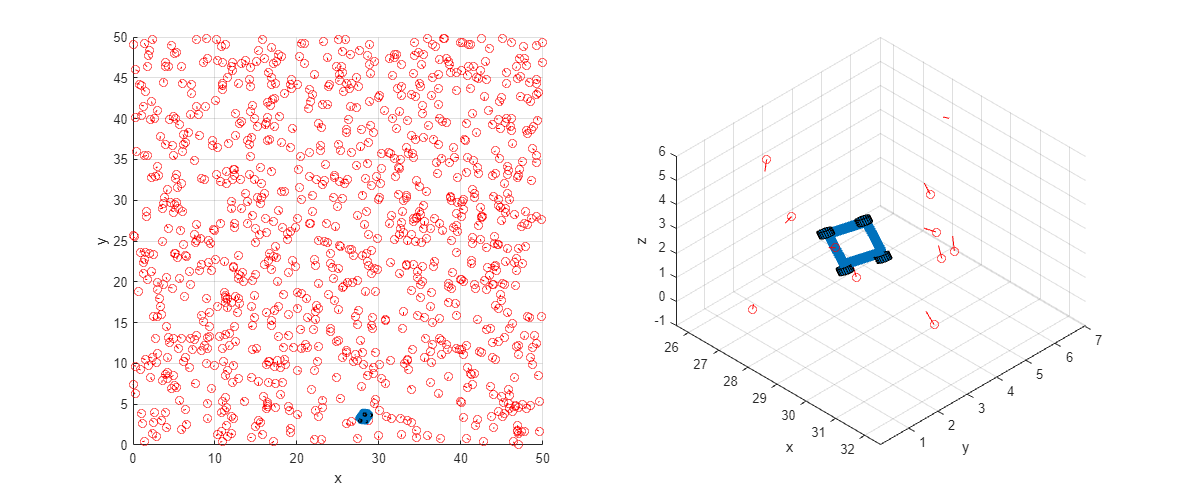
関数 plotRobot はこの例ではサポート ファイルとして提供され、部屋のトップダウン ビューおよびロボットと近くの対象物のクローズアップ ビューをプロットします。ロボットは車輪の付いた青いボックスで表され、対象物は向きを表す線を伴う赤い円で表されます。この関数を使用するには、ライブ スクリプトとして例を開きます。

関数 plotRobot を呼び出します。

plotRobot(Robot,Map)

方程式の定義

マップ上に存在する対象物を正確に識別するために、ロボットがマップを変換してセンサーを起点に配置する必要があります。こうすることによってロボットは、現在検知しているものとこれから検知するものとを比較して、マップ上の対象物を見つけられるようになります。

マップ上に存在する対象物 $$i$$ のグローバル マップでの位置情報を変換することで、ロボットを基準としてマップ上に存在するその対象物の相対位置 $$T_{rel}(i)$$ と向き $$R_{rel}(i)$$ を求めることができます。

ここで、$$T_{bot}$$ と $$R_{bot}$$ はロボットの位置と向きであり、$$T_{map}(i)$$ と $$R_{map}(i)$$ はマップ データを表します。これに相当する MATLAB コードは次のようになります。

Rrel(:,:,i) = Rbot' * Rmap(:,:,i)
Trel(:,i) = Rbot' * (Tmap(:,i) - Tbot)

for ループを使用して行列変換を CPU 上で実行

この例の最後に示しているサポート関数 loopingTransform は、すべての変換を順番にループ処理し、各対象物を、ロボットを基準とした位置に変換します。関数 zeros の名前と値の引数 like に注意してください。これにより、関数は、プロトタイプ配列と同じデータ型のゼロからなる配列を返します。たとえば、プロトタイプ配列が gpuArray の場合、zeros は gpuArray を返します。これにより、次のセクションで同じコードを GPU で使用できます。

関数timeitを使用して計算の時間を測定します。関数 timeit は loopingTransform の実行時間を複数回測定し、測定値の中央値を返します。timeit には引数をもたない関数が必要なため、@() 構文を使用して正しい形式の無名関数を作成します。

cpuTime = timeit(@()loopingTransform(Robot,Map,numFeatures))

cpuTime = 
0.0048

for ループを使用して行列変換を GPU 上で実行

GPU で同じコードを実行するには、入力データを関数にgpuArrayとして渡すだけです。gpuArray は GPU メモリに格納される配列を表します。MATLAB や他のツールボックスにある多数の関数が gpuArray オブジェクトをサポートしており、コードに最小限の変更を加えて GPU で実行することができます。詳細については、GPU での MATLAB 関数の実行を参照してください。

目的の GPU が使用可能で選択されていることを確認します。

gpu = gpuDevice;
disp(gpu.Name + " GPU selected.")

NVIDIA RTX A5000 GPU selected.

ロボットの位置と向きおよびマップ内の対象物が含まれた GPU 配列を作成します。

gMap.R = gpuArray(Map.R);
gMap.T = gpuArray(Map.T);
gRobot.R = gpuArray(Robot.R);
gRobot.T = gpuArray(Robot.T);

関数gputimeitを使用して計算の時間を測定します。関数 gputimeit は、GPU 計算を含むコードの timeit に相当します。時間を記録する前に、すべての GPU 演算が終了していることを確認します。

gpuTime = gputimeit(@()loopingTransform(gRobot,gMap,numFeatures))

gpuTime = 
0.1842

pagefun を使用して行列変換を GPU 上で実行

GPU を使用した方法では、すべての計算が独立しているにもかかわらず順番にしか実行されないため、非常に時間がかかります。pagefun を使用すると、すべての計算を並列に実行することができます。

この例の最後に示しているサポート関数 pagefunTransform は、for ループの代わりに pagefun を使用して関数 loopingTransform と同じ変換を適用します。初めの計算は、回転の計算です。これは行列乗算を含み、関数 mtimes (*) に変換されます。これを、乗算する 2 組の回転と共に pagefun に渡します。

Rel.R = pagefun(@mtimes,Robot.R',Map.R);

Robot.R' は 3 行 3 列の行列であり、Map.R は 3×3×N の配列です。関数 pagefun が、マップから得た個々の独立した行列をロボットの該当する回転に一致させ、必要な 3×3×N の出力を提供します。

また平行移動計算は行列乗算も含みますが、行列乗算の通常のルールでは、これを変更せずにループ外に出すことができます。

Rel.T = Robot.R' * (Map.T - Robot.T);

関数gputimeitを使用して計算の時間を測定します。

gpuPagefunTime = gputimeit(@()pagefunTransform(gRobot,gMap))

gpuPagefunTime = 
4.9757e-04

結果の比較

時間測定の結果をプロットします。

figure
labels = categorical(["CPU Execution","GPU Execution","GPU Execution with \fontname{consolas}pagefun"]);
bar(labels,[cpuTime,gpuTime,gpuPagefunTime])
ylabel("Execution Time (s)")
set(gca,YScale="log")

pagefun を使用した実行が CPU およびシンプルな GPU での実行よりどのくらい高速かを計算します。

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than on the CPU.\n", ...
    cpuTime/gpuPagefunTime);

Executing the transforms on the GPU using pagefun is 9.63 times faster than on the CPU.

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than using for-loops on the GPU.\n", ...
    gpuTime/gpuPagefunTime);

Executing the transforms on the GPU using pagefun is 370.29 times faster than using for-loops on the GPU.

考えられる複数のロボット位置を使用した行方不明のロボットの位置特定

ロボットがマップ上の不明な場所にいる場合、グローバル検索アルゴリズムを使用してロボット自身の位置を特定できます。このアルゴリズムは上記の計算を実行し、またロボットのセンサーによって確認済みの対象物と、その位置から確認できるであろうものとの間の有用な対応を検索することで考えられる位置情報を多数テストします。

考えられる複数のロボット位置および複数の対象物があります。N 個の対象物と M 個のロボットの場合、N*M の変換が必要です。'ロボットの空間' と '対象物の空間' を区別するために、回転に対しては 4 次元、並進に対しては 3 次元を使用します。つまり、ロボットの回転は 3×3×1×M、並進は 3×1×M となります。

10 箇所のランダムなロボット位置を使用して検索を初期化します。優れた検索アルゴリズムは位相的な手がかりまたはその他の手がかりを使用して、より高度な検索を設定します。

numRobots = 10;
Robot = randomTransforms(numRobots,roomDimensions);
Robot.R = reshape(Robot.R,3,3,1,[]); % Spread along the 4th dimension
Robot.T = reshape(Robot.T,3,1,[]); % Spread along the 3rd dimension

この例の最後で定義しているサポート関数 loopingTransform2 は、2 つの入れ子にされたループを使用してループ変換を実行することでロボットと対象物をループ処理します。

timeit を使用して計算の時間を測定します。

cpuTime = timeit(@()loopingTransform2(Robot,Map,numFeatures,numRobots))

cpuTime = 
0.0731

ロボットの回転および並進が含まれた GPU 配列を作成します。

gRobot.R = gpuArray(Robot.R);
gRobot.T = gpuArray(Robot.T);

gputimeit を使用して GPU での計算の時間を測定します。

gpuTime = gputimeit(@() loopingTransform2(gRobot,gMap,numFeatures,numRobots))

gpuTime = 
2.1571

既に述べたように、ループによる方法を GPU 上で実行した場合、計算を並列に行わないため速度は非常に遅くなります。

この例の最後に示しているサポート関数 pagefunTransform2 は、入れ子にされた for ループの代わりに pagefun の呼び出しを 2 つ使用して関数 loopingTransform2 と同じ変換を適用します。この関数では、mtimes に加えて transpose 演算子も pagefun の呼び出しに組み込む必要があります。また、この関数は関数 squeeze を転置されたロボットの向きに適用し、拡張をロボットに適用して 3 次元にし、並進と一致させます。上記にもかかわらず、結果のコードはかなりコンパクトになります。

関数 pagefun は次元を適切に拡張します。したがって、3×3×1×M の行列 Rt と 3×3×N×1 の行列 Map.R を乗算した場合には、3×3×N×M の行列が出力されます。

gputimeit を使用して GPU での計算の時間を測定します。

gpuPagefunTime = gputimeit(@()pagefunTransform2(gRobot,gMap))

gpuPagefunTime = 
0.0016

結果の比較

時間測定の結果をプロットします。

labels = categorical(["CPU Execution","GPU Execution","GPU Execution with \fontname{consolas}pagefun"]);
bar(labels,[cpuTime,gpuTime,gpuPagefunTime])
ylabel("Execution Time (s)")
set(gca,YScale="log")

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than on the CPU.\n", ...
    cpuTime/gpuPagefunTime);

Executing the transforms on the GPU using pagefun is 45.61 times faster than on the CPU.

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than using nested for-loops on the GPU.\n", ...
    gpuTime/gpuPagefunTime);

Executing the transforms on the GPU using pagefun is 1346.60 times faster than using nested for-loops on the GPU.

まとめ

関数 pagefun は、arrayfun がサポートする大部分のスカラー演算に加えて、多くの 2 次元演算をサポートします。これらの関数を一緒に使用することで、行列代数や配列操作などの幅広い計算をベクトル化できるようになります。そのためループの必要がなくなり、パフォーマンスが大幅に向上します。

いずれの場所で GPU データに対して小規模な計算をループで行っている場合でも、この方法によるベクトル化された実装への転換を検討するようお勧めします。このようにすることで、それまでパフォーマンスの改善が見られなかった場所で、GPU を最大限に利用してパフォーマンスを向上させる機会が得られることもあります。

サポート関数

ランダム変換関数

関数 randomTransforms は、指定された次元の部屋で N 個のランダムな変換を定義する行列を作成します。各変換は、ランダムな並進 T およびランダムな回転 R で構成されます。この関数を使用して、部屋内の対象物のマップおよびロボットの開始位置と向きを設定できます。

function Tform = randomTransforms(N,roomDimensions)
% Preallocate matrices.
Tform.T = zeros(3,N);
Tform.R = zeros(3,3,N);

for i = 1:N
    % Create random translation.
    Tform.T(:,i) = rand(3,1) .* roomDimensions';

    % Create random rotation by extracting an orthonormal
    % basis from a random 3-by-3 matrix.
    Tform.R(:,:,i) = orth(rand(3,3));
end

end

ループ変換関数

関数 loopingTransform は、変換を順番にループ処理することで、各対象物の位置をロボットに対する相対的な位置に変換します。

function Rel = loopingTransform(Robot,Map,numFeatures)
% Preallocate matrices.
Rel.R = zeros(size(Map.R),like=Map.R);
Rel.T = zeros(size(Map.T),like=Map.T);

for i = 1:numFeatures
    % Find orientation of map feature relative to the robot.
    Rel.R(:,:,i) = Robot.R' * Map.R(:,:,i);
    % Find position of map feature relative to the robot.
    Rel.T(:,i) = Robot.R' * (Map.T(:,i) - Robot.T);
end

end

pagefun 変換関数

関数 pagefunTransform は、関数 pagefun を使用して変換を適用することで、各対象物の位置をロボットに対する相対的な位置に変換します。

function Rel = pagefunTransform(Robot,Map)
% Find orientation of map feature relative to the robot.
Rel.R = pagefun(@mtimes,Robot.R', Map.R);
% Apply translation.
Rel.T = Robot.R' * (Map.T - Robot.T);
end

入れ子にされたループ変換関数

関数 loopingTransform2 は、2 つの入れ子にされたループを使用してループ変換を実行することでロボットと対象物をループ処理します。この変換で、各対象物の位置を各ロボットに対する相対的な位置にマッピングします。

function Rel = loopingTransform2(Robot,Map,numFeatures,numRobots)
% Preallocate matrices.
Rel.R = zeros(3,3,numFeatures,numRobots,like=Map.R);
Rel.T = zeros(3,numFeatures,numRobots,like=Map.T);

for i = 1:numFeatures
    for j = 1:numRobots
        % Find orientation of map feature relative to the robot.
        Rel.R(:,:,i,j) = Robot.R(:,:,1,j)' * Map.R(:,:,i);
        % Find position of map feature relative to the robot.
        Rel.T(:,i,j) = ...
            Robot.R(:,:,1,j)' * (Map.T(:,i) - Robot.T(:,1,j));
    end
end

end

pagefun の呼び出しを 2 つ使用した変換関数

関数 pagefunTransform2 は、関数 pagefun の呼び出しを 2 つ使用することで、各対象物の位置を各ロボットに対する相対的な位置にマッピングします。

function Rel = pagefunTransform2(Robot,Map)
% Find orientation of map feature relative to the robot.
Rt = pagefun(@transpose,Robot.R);
Rel.R = pagefun(@mtimes,Rt,Map.R);
% Find position of map feature relative to the robot.
Rel.T = pagefun(@mtimes,squeeze(Rt), ...
    (Map.T - Robot.T));
end