Symbolic Math Toolbox を使用した勾配とヘッシアンの計算

この例では次を使用します。

この例では、fmincon と Symbolic Math Toolbox™ の関数を併用して、非線形最適化問題をより迅速かつロバストに解く方法を説明します。Symbolic Math Toolbox のライセンスをお持ちの場合は、以下の Symbolic Math Toolbox 関数を使用して、目的関数と制約関数の解析勾配とヘッシアンを簡単に計算できます。

jacobian (Symbolic Math Toolbox)は、スカラー関数の勾配を生成し、ベクトル関数の偏導関数の行列を生成します。そのため、たとえば、jacobian を勾配に適用することにより、ヘッセ行列 (目的関数の 2 次導関数) を取得することができます。この例では、目的関数と制約関数のシンボリックな勾配とヘッシアンを生成するためにどのように jacobian を使用するかを示します。
matlabFunction (Symbolic Math Toolbox)は、シンボリック表現式の値を計算する無名関数またはファイルのどちらかを生成します。この例では、目的関数と制約関数を評価するファイルとその任意の点における導関数を生成するためにどのように matlabFunction を使用するかを示します。

Symbolic Math Toolbox 関数では、Optimization Toolbox™ 関数とは異なる構文と構造体が使用されます。特に、シンボリック変数は実数または複素数のスカラーですが、Optimization Toolbox 関数はベクトル引数を渡します。そのため、目的関数、制約、およびそのすべての必須導関数を fmincon の内点法アルゴリズムに適した形式でシンボリックに生成するためには、いくつかの手順を実行する必要があります。

問題ベースの最適化は、勾配を自動的に計算して使用できます。Optimization Toolbox の自動微分を参照してください。自動微分を使用したこの問題に対する問題ベースのアプローチについては、最適化変数を使用した静電学における制約付き非線形最適化を参照してください。

問題の説明

10 個の電子を導電体に置く静電学問題を考えてみましょう。電子は、導電体内に存在する制約に従い、その総位置エネルギーを最小化するように整列します。すべての電子は最小値で導電体の境界上にあります。電子は区別できないため、この問題の固有の最小値が存在しません (1 つの解で電子を並べ替えれば、別の有効な解になります)。この例は、Dolan、Moré、Munson [58]に基づきます。

この例は、次の不等式によって定義される導電体です。

$z \leq - | x | - | y |$

$x^{2} + y^{2} + (z + 1)^{2} \leq 1$ .

この導電体は球の上の角錐のように見えます。

[X,Y] = meshgrid(-1:.01:1);
Z1 = -abs(X) - abs(Y);
Z2 = -1 - sqrt(1 - X.^2 - Y.^2);
Z2 = real(Z2);
W1 = Z1; W2 = Z2;
W1(Z1 < Z2) = nan; % Only plot points where Z1 > Z2
W2(Z1 < Z2) = nan; % Only plot points where Z1 > Z2
hand = figure; % Handle to the figure, for more plotting later
set(gcf,'Color','w') % White background
surf(X,Y,W1,'LineStyle','none');
hold on
surf(X,Y,W2,'LineStyle','none');
view(-44,18)

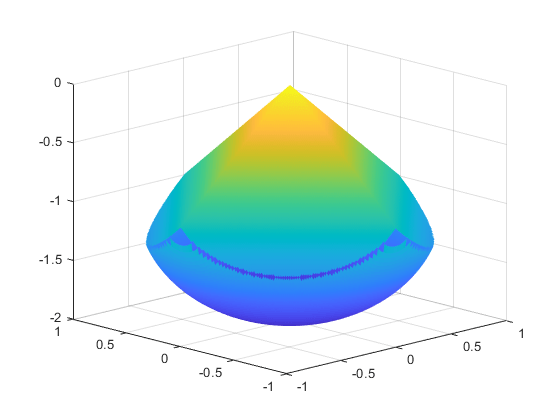
形状の上と下の表面の間にわずかな隙間があります。この隙間は、形状を作成するために使用された一般的なプロットルーチンの人工物です。このルーチンは、他の面に触れる 1 面上の四角形の領域を消去します。

変数の作成

真にシンボリックな変数 xij (i は 1 ～ 10、j は 1 ～ 3) で構成される 30 行 1 列のベクトルとして、シンボリックなベクトル x を生成します。これらの変数は電子 i の 3 つの座標を表します。xi1 は $x$ 座標に、xi2 は $y$ 座標に、xi3 は $z$ 座標に対応します。

x = cell(3, 10);
for i = 1:10
    for j = 1:3
        x{j,i} = sprintf('x%d%d',i,j);
    end
end
x = x(:); % Now x is a 30-by-1 vector
x = sym(x, 'real');

ベクトル x を表示します。

x = 
 $(\begin{array}{c} x_{11} \\ x_{12} \\ x_{13} \\ x_{21} \\ x_{22} \\ x_{23} \\ x_{31} \\ x_{32} \\ x_{33} \\ x_{41} \\ x_{42} \\ x_{43} \\ x_{51} \\ x_{52} \\ x_{53} \\ x_{61} \\ x_{62} \\ x_{63} \\ x_{71} \\ x_{72} \\ x_{73} \\ x_{81} \\ x_{82} \\ x_{83} \\ x_{91} \\ x_{92} \\ x_{93} \\ x_{101} \\ x_{102} \\ x_{103} \end{array})$

線形制約を含める

次の線形制約を記述します。

$z \leq - | x | - | y |$

これは各電子の 4 つのセットの線形不等式です。

xi3 - xi1 - xi2 ≤ 0
xi3 - xi1 + xi2 ≤ 0
xi3 + xi1 - xi2 ≤ 0
xi3 + xi1 + xi2 ≤ 0

そのため、この問題には全部で 40 の線形不等式が含まれています。

体系的に不等式を記述します。

B = [1,1,1;-1,1,1;1,-1,1;-1,-1,1];

A = zeros(40,30);
for i=1:10
    A(4*i-3:4*i,3*i-2:3*i) = B;
end

b = zeros(40,1);

A*x ≤ b が不等式を表すことがわかります。

disp(A*x)

 $(\begin{array}{c} x_{11} + x_{12} + x_{13} \\ x_{12} - x_{11} + x_{13} \\ x_{11} - x_{12} + x_{13} \\ x_{13} - x_{12} - x_{11} \\ x_{21} + x_{22} + x_{23} \\ x_{22} - x_{21} + x_{23} \\ x_{21} - x_{22} + x_{23} \\ x_{23} - x_{22} - x_{21} \\ x_{31} + x_{32} + x_{33} \\ x_{32} - x_{31} + x_{33} \\ x_{31} - x_{32} + x_{33} \\ x_{33} - x_{32} - x_{31} \\ x_{41} + x_{42} + x_{43} \\ x_{42} - x_{41} + x_{43} \\ x_{41} - x_{42} + x_{43} \\ x_{43} - x_{42} - x_{41} \\ x_{51} + x_{52} + x_{53} \\ x_{52} - x_{51} + x_{53} \\ x_{51} - x_{52} + x_{53} \\ x_{53} - x_{52} - x_{51} \\ x_{61} + x_{62} + x_{63} \\ x_{62} - x_{61} + x_{63} \\ x_{61} - x_{62} + x_{63} \\ x_{63} - x_{62} - x_{61} \\ x_{71} + x_{72} + x_{73} \\ x_{72} - x_{71} + x_{73} \\ x_{71} - x_{72} + x_{73} \\ x_{73} - x_{72} - x_{71} \\ x_{81} + x_{82} + x_{83} \\ x_{82} - x_{81} + x_{83} \\ x_{81} - x_{82} + x_{83} \\ x_{83} - x_{82} - x_{81} \\ x_{91} + x_{92} + x_{93} \\ x_{92} - x_{91} + x_{93} \\ x_{91} - x_{92} + x_{93} \\ x_{93} - x_{92} - x_{91} \\ x_{101} + x_{102} + x_{103} \\ x_{102} - x_{101} + x_{103} \\ x_{101} - x_{102} + x_{103} \\ x_{103} - x_{102} - x_{101} \end{array})$

非線形制約とその勾配とヘッシアンの作成

非線形制約も構造化されます。

$x^{2} + y^{2} + (z + 1)^{2} \leq 1$ .

制約とその勾配とヘッシアンを生成します。

c = sym(zeros(1,10));
i = 1:10;
c = (x(3*i-2).^2 + x(3*i-1).^2 + (x(3*i)+1).^2 - 1).';

gradc = jacobian(c,x).'; % .' performs transpose

hessc = cell(1, 10);
for i = 1:10
    hessc{i} = jacobian(gradc(:,i),x);
end

制約ベクトル c は行ベクトルです。c(i) の勾配は、行列 gradc の i 列目に示されます。非線形制約で説明されているように、この形式が正しいです。

ヘッセ行列 hessc{1}, ..., hessc{10} は、平方で対称的です。この例では、これらが cell 配列に保存されます。この方が hessc1、...、hessc10 などの別々の変数に保存するよりも効率的です。

.' 構文を使用して、転置します。構文 ' は、異なるシンボリック導関数をもつ共役転置を意味します。

目的関数とその勾配およびヘッシアンの作成

目的関数 (位置エネルギー) は、各電子ペアの間の距離の逆数の合計です。

$e n e r g y = \sum_{i < j} \frac{1}{| x_{i} - x_{j} |}$ .

距離はベクトルの成分にある差分の平方の合計の平方根です。

エネルギー (目的関数) とその勾配およびヘッシアンを計算します。

energy = sym(0);
for i = 1:3:25
    for j = i+3:3:28
        dist = x(i:i+2) - x(j:j+2);
        energy = energy + 1/sqrt(dist.'*dist);
    end
end

gradenergy = jacobian(energy,x).';

hessenergy = jacobian(gradenergy,x);

目的関数ファイルの作成

目的関数の出力は energy と gradenergy の 2 つです。matlabFunction を呼び出す際に、両方の関数を 1 つのベクトルに入れます。matlabFunction が生成する部分表現の数が減り、呼び出す関数 (この例では fmincon) が両方の出力を要求する時にのみ、勾配が返されます。生成されたファイルは、MATLAB パス上の任意のフォルダーに配置できます。この場合は、現在のフォルダーに配置します。

currdir = [pwd filesep]; % You might need to use currdir = pwd 
filename = [currdir,'demoenergy.m'];
matlabFunction(energy,gradenergy,'file',filename,'vars',{x});

matlabFunction は、最初の出力として energy を、2 番目の出力として gradenergy を返します。また、この関数は、入力 x11、...、x103 のリストの代わりに、単一の入力ベクトル {x} を取ります。

生成されたファイル demoenergy.m は、以下の行か同様の行を含みます。

function [energy,gradenergy] = demoenergy(in1)
%DEMOENERGY
%   [ENERGY,GRADENERGY] = DEMOENERGY(IN1)
...
x101 = in1(28,:);
...
energy = 1./t140.^(1./2) + ...;
if nargout > 1
    ...
    gradenergy = [(t174.*(t185 - 2.*x11))./2 - ...];
end

この関数は勾配をもつ目的関数のための正しい形式をもちます (スカラー目的関数の記述を参照)。

制約関数ファイルの作成

非線形制約関数を生成し、それを正しい形式にします。

filename = [currdir,'democonstr.m'];
matlabFunction(c,[],gradc,[],'file',filename,'vars',{x},...
    'outputs',{'c','ceq','gradc','gradceq'});

生成されたファイル democonstr.m は、以下の行か同様の行を含みます。

function [c,ceq,gradc,gradceq] = democonstr(in1)
%DEMOCONSTR
%    [C,CEQ,GRADC,GRADCEQ] = DEMOCONSTR(IN1)
...
x101 = in1(28,:);
...
c = [t417.^2 + ...];
if nargout > 1
    ceq = [];
end
if nargout > 2
    gradc = [2.*x11,...];
end
if nargout > 3
    gradceq = [];
end

この関数は勾配をもつ制約関数のための正しい形式をもちます (非線形制約を参照)。

ヘッセファイルの生成

問題のラグランジュ関数のヘッシアンを生成するには、まず、エネルギーヘッシアンと制約ヘッシアン用のファイルを生成します。

目的関数 hessenergy のヘッシアンは、大きなシンボリック表現であり、size(char(hessenergy)) の評価が示すように、150,000 を超えるシンボルが含まれています。そのため、matlabFunction(hessenergy) の実行には、長い時間がかかります。

ファイル hessenergy.m を生成します。

filename = [currdir,'hessenergy.m'];
matlabFunction(hessenergy,'file',filename,'vars',{x});

その反対に制約関数のヘッシアンは小さく、計算に時間がかかりません。

for i = 1:10
    ii = num2str(i);
    thename = ['hessc',ii];
    filename = [currdir,thename,'.m'];
    matlabFunction(hessc{i},'file',filename,'vars',{x});
end

目的と制約用のすべてのファイルを生成したら、それらを適切なラグランジュ乗数とともに補助関数 hessfinal.m に配置します (この例の最後にコードが掲載されています)。

最適化の実行

[0,0,–1] でセンタリングされた半径 1/2 の球上で無作為に分布された電子で最適化を開始します。

rng default % For reproducibility
Xinitial = randn(3,10); % Columns are normal 3-D vectors
for j=1:10
    Xinitial(:,j) = Xinitial(:,j)/norm(Xinitial(:,j))/2;
    % This normalizes to a 1/2-sphere
end
Xinitial(3,:) = Xinitial(3,:) - 1; % Center at [0,0,-1]
Xinitial = Xinitial(:); % Convert to a column vector

interior-point アルゴリズムを使用し、勾配とヘッシアンを使用するようにオプションを設定します。

options = optimoptions(@fmincon,'Algorithm','interior-point','SpecifyObjectiveGradient',true,...
    'SpecifyConstraintGradient',true,'HessianFcn',@hessfinal,'Display','final');

fmincon を呼び出します。

[xfinal,fval,exitflag,output] = fmincon(@demoenergy,Xinitial,...
    A,b,[],[],[],[],@democonstr,options);

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

目的関数値、終了フラグ、反復の回数、関数評価の回数を表示します。

disp(fval)

   34.1365

disp(exitflag)

disp(output.iterations)

disp(output.funcCount)

電子の初期の位置が無作為でも、最終的な位置はほぼ対称になります。

for i = 1:10
    plot3(xfinal(3*i-2),xfinal(3*i-1),xfinal(3*i),'r.','MarkerSize',25);
end

3 次元ジオメトリ全体を調査するために、Figure を回転させます。

rotate3d

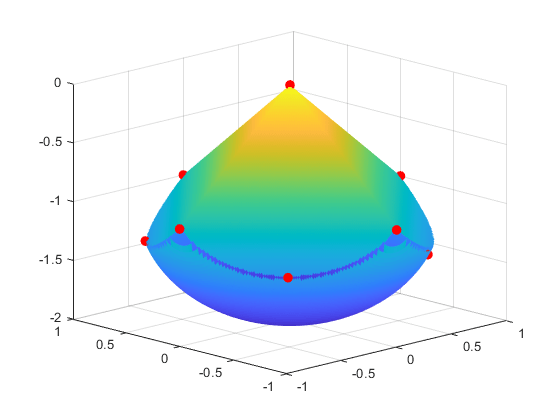
figure(hand)

勾配とヘッシアンなしの最適化と比較

勾配とヘッシアンを使用すると、最適化をより速くより正確に実行できます。勾配やヘッシアン情報を使用しない同じ最適化と比較するために、勾配とヘッシアンを使用しないようにオプションを設定します。

options = optimoptions(@fmincon,'Algorithm','interior-point',...
    'Display','final');
[xfinal2,fval2,exitflag2,output2] = fmincon(@demoenergy,Xinitial,...
    A,b,[],[],[],[],@democonstr,options);

Feasible point with lower objective function value found.


Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

目的関数値、終了フラグ、反復の回数、関数評価の回数を表示します。

disp(fval2)

   34.1365

disp(exitflag2)

disp(output2.iterations)

disp(output2.funcCount)

導関数情報を使用する場合と使用しない場合で、反復の回数および関数評価の回数を比較します。

tbl = table([output.iterations;output2.iterations],[output.funcCount;output2.funcCount],...
    'RowNames',{'With Derivatives','Without Derivatives'},'VariableNames',{'Iterations','Fevals'})

tbl=2×2 table
                           Iterations    Fevals
                           __________    ______

    With Derivatives           19           28 
    Without Derivatives        77         2434

シンボリックな変数前提条件をクリア

この例のシンボリックな変数は、シンボリックなエンジンワークスペース内でそれらが実数であることを前提とします。変数を削除しても、シンボリックエンジンワークスペースからこの前提は取り除かれません。syms を使用して、変数の前提をクリアします。

syms x

仮定が空になっていることを確認します。

assumptions(x)

 
ans =
 
Empty sym: 1-by-0

補助関数

次のコードは補助関数 hessfinal を作成します。

function H = hessfinal(X,lambda)
%
% Call the function hessenergy to start
H = hessenergy(X);

% Add the Lagrange multipliers * the constraint Hessians
H = H + hessc1(X) * lambda.ineqnonlin(1);
H = H + hessc2(X) * lambda.ineqnonlin(2);
H = H + hessc3(X) * lambda.ineqnonlin(3);
H = H + hessc4(X) * lambda.ineqnonlin(4);
H = H + hessc5(X) * lambda.ineqnonlin(5);
H = H + hessc6(X) * lambda.ineqnonlin(6);
H = H + hessc7(X) * lambda.ineqnonlin(7);
H = H + hessc8(X) * lambda.ineqnonlin(8);
H = H + hessc9(X) * lambda.ineqnonlin(9);
H = H + hessc10(X) * lambda.ineqnonlin(10);
end