非線形最小二乗法、問題ベース

この例では、問題ベースの最適化ワークフローを使用して、非線形最小二乗曲線近似を行う方法を示します。

モデル

この問題に対するモデルの方程式は次のとおりです。

$y (t) = A_{1} \exp (r_{1} t) + A_{2} \exp (r_{2} t),$

ここで、 $A_{1}$ 、 $A_{2}$ 、 $r_{1}$ 、 $r_{2}$ は未知のパラメーターです。 $y$ は応答、 $t$ は時間です。この問題には、時間のデータ tdata と (ノイズを含む) 応答測定値 ydata が必要です。ゴールは、最適な $A$ と $r$ 、つまり以下を最小化する値を求めることです。

$\sum_{t \in t d a t a} {(y (t) - y d a t a)}^{2} .$

サンプルデータ

問題には通常、データがあります。ここでは、問題のために、ノイズを含む人為的なデータを生成します。基となる値として A = [1,2] と r = [-1,-3] を使用し、時間データとして 0 ～ 3 の 200 個の乱数値を使用します。得られたデータ点をプロットします。

rng default % For reproducibility
A = [1,2];
r = [-1,-3];
tdata = 3*rand(200,1);
tdata = sort(tdata); % Increasing times for easier plotting
noisedata = 0.05*randn(size(tdata)); % Artificial noise
ydata = A(1)*exp(r(1)*tdata) + A(2)*exp(r(2)*tdata) + noisedata;
plot(tdata,ydata,'r*')
xlabel 't'
ylabel 'Response'

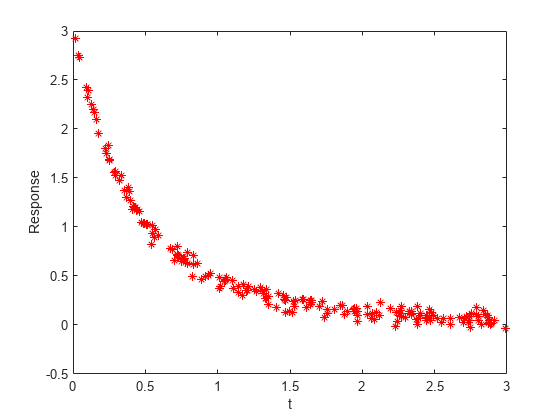
Figure contains an axes object. The axes object with xlabel t, ylabel Response contains a line object which displays its values using only markers.

データにはノイズが多く含まれています。そのため、解はおそらく、元のパラメーター A および r とは一致しません。

問題ベースのアプローチ

最適適合パラメーター A および r を求めるには、まずこれらの名前をもつ最適化変数を定義します。

A = optimvar('A',2);
r = optimvar('r',2);

目的関数の式を作成します。これは、最小化する二乗和です。

fun = A(1)*exp(r(1)*tdata) + A(2)*exp(r(2)*tdata);
obj = sum((fun - ydata).^2);

目的関数 obj を使用して最適化問題を作成します。

lsqproblem = optimproblem("Objective",obj);

問題ベースのアプローチの場合、初期点を構造体として指定します。変数名は構造体のフィールドとします。初期値 A = [1/2,3/2] と初期値 r = [-1/2,-3/2] を指定します。

x0.A = [1/2,3/2];
x0.r = [-1/2,-3/2];

問題の定式化を確認します。

show(lsqproblem)

  OptimizationProblem : 

	Solve for:
       A, r

	minimize :
       sum(arg6)

       where:

           arg5 = extraParams{3};
           arg6 = (((A(1) .* exp((r(1) .* extraParams{1}))) + (A(2) .* exp((r(2) .* extraParams{2})))) - arg5).^2;

       extraParams

問題ベースの解

問題を解きます。

[sol,fval] = solve(lsqproblem,x0)

Solving problem using lsqnonlin.

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

<stopping criteria details>

sol = struct with fields:
    A: [2×1 double]
    r: [2×1 double]

fval = 
0.4724

得られた解と元のデータをプロットします。

figure
responsedata = evaluate(fun,sol);
plot(tdata,ydata,'r*',tdata,responsedata,'b-')
legend('Original Data','Fitted Curve')
xlabel 't'
ylabel 'Response'
title("Fitted Response")

Figure contains an axes object. The axes object with title Fitted Response, xlabel t, ylabel Response contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Original Data, Fitted Curve.

プロットは、当てはめたデータが、ノイズを含む元のデータとよく一致していることを示しています。

当てはめたパラメーターが元のパラメーター A = [1,2] および r = [-1,-3] とどのくらい近いか確認します。

disp(sol.A)

    1.1615
    1.8629

disp(sol.r)

   -1.0882
   -3.2256

当てはめたパラメーターのずれは、A では 15%、r では 8% です。

`fcn2optimexpr` を必要とするサポートされていない関数

目的関数が初等関数で構成されていない場合、fcn2optimexprを使用して、その関数を最適化式に変換しなければなりません。非線形関数から最適化式への変換を参照してください。次に例を示します。

fun = @(A,r) A(1)*exp(r(1)*tdata) + A(2)*exp(r(2)*tdata);
response = fcn2optimexpr(fun,A,r);
obj = sum((response - ydata).^2);

問題解法の残りの手順は同じです。その他の違いはプロットルーチンのみであり、次のように fun の代わりに response を呼び出します。

responsedata = evaluate(response,sol);

サポートされている関数の一覧については、最適化変数および式でサポートされる演算を参照してください。

参考

solve

トピック

問題ベースの最適化ワークフロー