ヤコビ スパース パターンを使用した大規模連立非線形方程式
この例では、ヤコビ スパース パターンを指定して、大規模スパース連立方程式を効率的に解く方法を示します。この例では、n 個の連立方程式として定義された目的関数を使用します。
解く方程式は、, です。この例では、 を使用します。この例の最後にある nlsf1a 補助関数が目的関数 を実装します。
同じ方程式を解くヤコビアンを使用した大規模スパース連立非線形方程式 の例では、目的関数に明示的なヤコビアンが含まれています。ただし、ヤコビアンを明示的に計算できない場合がありますが、ヤコビアンのどの成分が非ゼロかを判断することはできます。この例では、ヤコビアンは三重対角です。これは、 の定義に現れる変数が 、、および だけだからです。したがって、ヤコビアンの非ゼロ部分は、主対角線とその 2 つの隣接する対角線上にしか存在しません。ヤコビ スパース パターンは、非ゼロ成分がヤコビアンの (潜在的な) 非ゼロ成分に対応する行列です。
ヤコビ スパース パターンを表すスパース x 三重対角行列を作成します。(このコード説明については、spdiagsを参照してください。)
n = 1000; e = ones(n,1); Jstr = spdiags([e e e],-1:1,n,n);
Jstr の構造を表示します。
spy(Jstr)
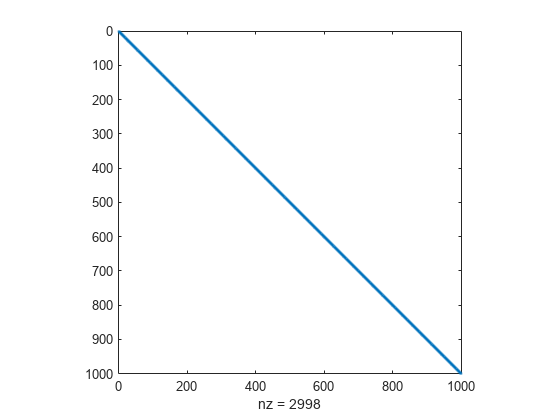
'trust-region' アルゴリズムを使用するように fsolve オプションを設定します。このアルゴリズムは、ヤコビ スパース パターンを利用可能な唯一の fsolve アルゴリズムです。
options = optimoptions('fsolve','Algorithm','trust-region','JacobPattern',Jstr);
初期点 x0 を -1 エントリのベクトルに設定します。
x0 = -1*ones(n,1);
問題を解きます。
[x,fval,exitflag,output] = fsolve(@nlsf1a,x0,options);
Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
結果の残差ノルムと fsolve が実行した関数評価の回数を調査します。
disp(norm(fval))
1.0522e-09
disp(output.funcCount)
25
残差ノルムはほぼ 0 ですが、これは、fsolve が問題を正しく解いたことを示しています。関数評価の回数は、かなり減少し、わずか 20 回程度です。この関数評価回数を、指定されたヤコビ スパース パターンを使用しない場合の回数と比較します。
options = optimoptions('fsolve','Algorithm','trust-region'); [x,fval,exitflag,output] = fsolve(@nlsf1a,x0,options);
Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
disp(norm(fval))
1.0659e-09
disp(output.funcCount)
5005
ソルバーは、原則、以前と同じ解に辿り着きますが、そのための関数評価は何千回にも及びます。
補助関数
次のコードは、nlsf1a 補助関数を作成します。
function F = nlsf1a(x) % Evaluate the vector function n = length(x); F = zeros(n,1); i = 2:(n-1); F(i) = (3-2*x(i)).*x(i)-x(i-1)-2*x(i+1) + 1; F(n) = (3-2*x(n)).*x(n)-x(n-1) + 1; F(1) = (3-2*x(1)).*x(1)-2*x(2) + 1; end