問題ベースの Optimize ライブ エディター タスクを使用した実行可能性

問題の説明

この例では、Optimize ライブ エディター タスクを使用して、さまざまなソルバーで実行可能点を見つける方法を示します。問題は、以下の制約を満たす点 $$[x,y]$$ を見つけることです。

$$(y+x^2{)}^2+0.1y^2\le 1$$

$$y\le \exp (-x)-3$$

$$y\le x-4$$.

制約関数がゼロに等しくなる曲線をグラフにします。領域のどの部分が実行可能 (負の制約関数値) であるかを確認するため、制約関数が –1/2 に等しい曲線をプロットします。関数 plotobjconstr (このスクリプトの終わりに掲載) を使用します。

plotobjconstr

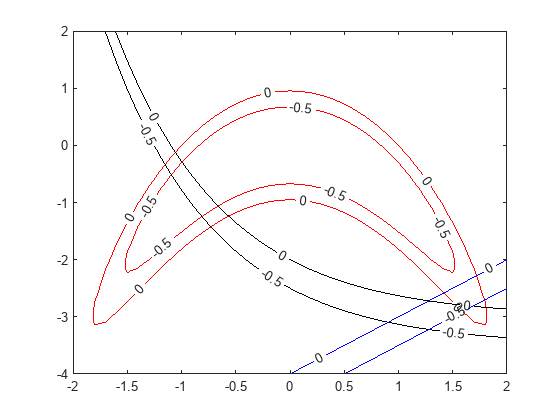
$$x=1.75,y=-3$$ の付近に、実行可能な領域が少しあるようです。すべての制約値が –1/2 より小さい場合は点がないため、実行可能なセットが小さいことに注意してください。

問題ベースの Optimize ライブ エディター タスクの使用

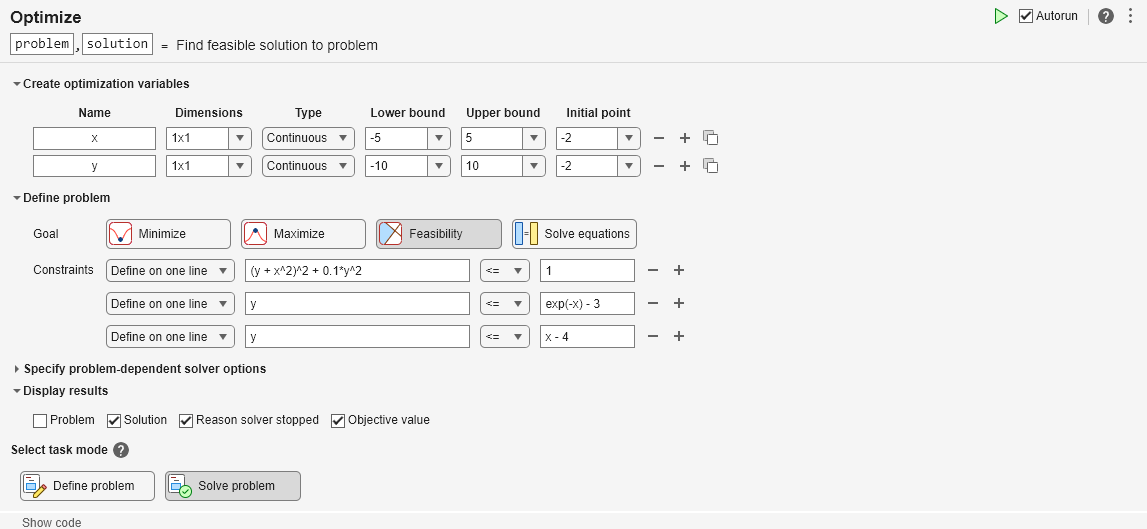
実行可能点を見つけるには、[コード] タブまたは [挿入] タブで [タスク] > [最適化] を選択して、ライブ スクリプトから Optimize ライブ エディター タスクを起動します。問題ベースのタスクを選択します。

問題変数 x を、下限が –5、上限が 5 となるように設定します。問題変数 y を、下限が –10、上限が 10 となるように設定します。x の初期点を 2、y の初期点を –2 に設定します。

[ゴール] を [実行可能性] に設定します。

3 つの制約を表す不等式を作成します。下記の図と一致するタスクとなっている必要があります。

タスク モードを [問題の求解] に切り替えます。タスクは fmincon ソルバーを選択し、次の解に到達します。

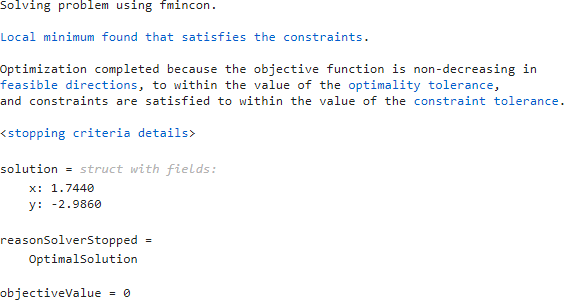
初期点の効果

別の初期点から開始すると、fmincon が解を見つけられない場合があります。x の初期点を –2 に設定します。

今回、fmincon は実行可能解に到達できません。

別のソルバーの試行

求解を試みるために、別のソルバーを試します。ソルバーを ga に設定します。そのため、[問題に応じたソルバー オプションの指定] 展開リンクのソルバーを指定します。ソルバーの進行状況を監視するため、プロット関数を [最大制約違反] に設定します。

ga は、制約の許容誤差内で実行可能点を見つけます。

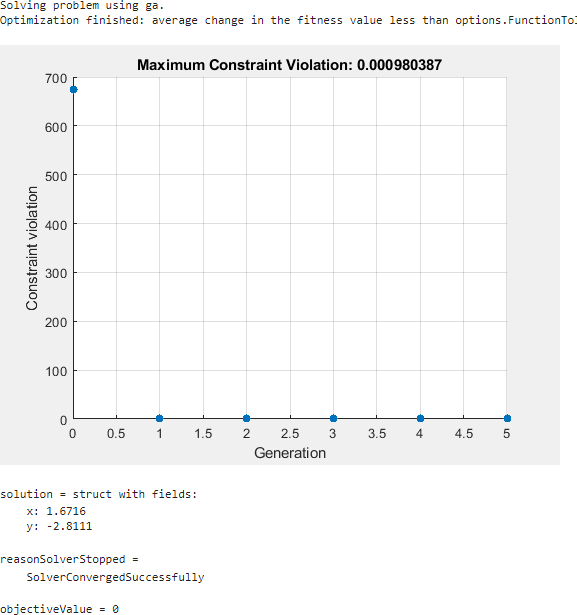
ga は、fmincon とは異なる解を見つけます。この解はやや実行不可能です。実行不可能性がより低い解を得るには、制約の許容誤差オプションを既定値より小さい値に設定します。あるいは、別のソルバーを試します。

surrogateopt の試行

surrogateopt ソルバーの使用を試します。プロット関数を [最大制約違反] に設定します。この設定は、ga の解から自動的に引き継がれません。

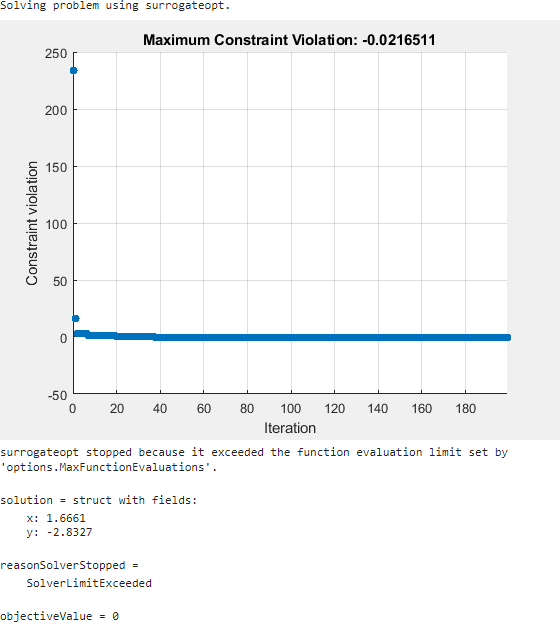
surrogateopt は実行可能解に到達しますが、初めて解に到達したときは停止しません。代わりに、surrogateopt はその関数評価の制限に到達するまで反復を続けます。反復を早めに停止するには、最大制約違反が 1e-6 以下に到達すると直ちにソルバーを停止する出力関数を指定します。このようにすると、ソルバーがもっと早く停止します。補助関数 surrout (このスクリプトの終わりに掲載) を使用します。この関数を指定するには、関数に対する関数ハンドルを作成します。

outfun = @surrout;

[問題に応じたソルバー オプションの指定] > [オプション] > [診断] > [出力関数] ドロップダウン メニューで関数ハンドルを指定します。

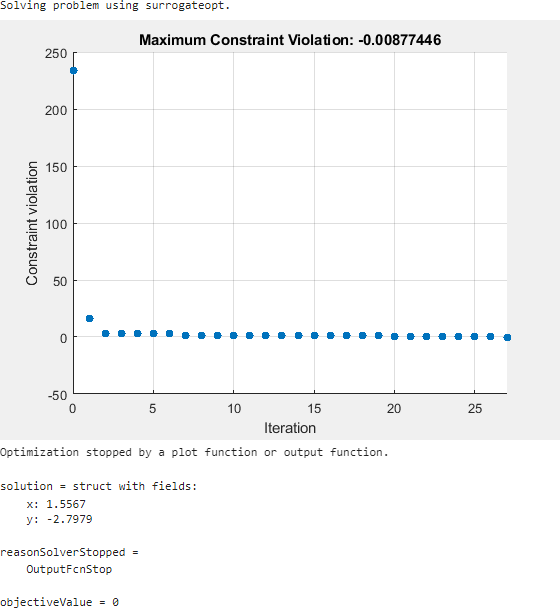
今回、ソルバーは 200 回ではなく約 30 回の関数評価の後に停止します。この解は前回の解とは少し異なりますが、どちらも実行可能解です。

結論

問題ベースの Optimize ライブ エディター タスクを使用することにより、fmincon および surrogateopt などの異なる構文のソルバーであっても、さまざまなソルバーを問題に対して使用してみることができます。また、このタスクはプロット関数の設定と他のオプションの設定にも役立ちます。

タスクの最終的な状態を下記の図に示します。さまざまなソルバーとオプションを使用して、自由に試してください。

Solving problem using surrogateopt.

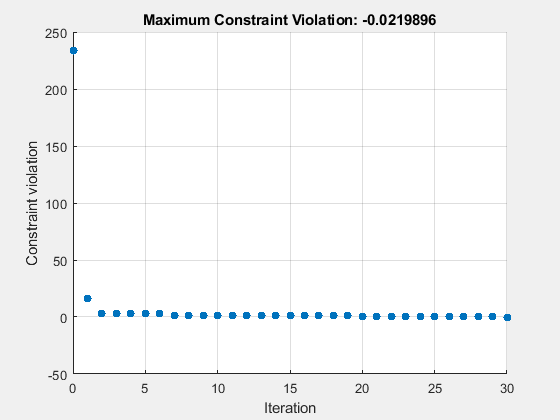
Optimization stopped by a plot function or output function.

solution = struct with fields:
    x: 1.5639
    y: -2.8127

reasonSolverStopped = 
    OutputFcnStop

objectiveValue = 0

補助関数

次のコードは、補助関数 plotobjconstr を作成します。

function plotobjconstr
[XX,YY] = meshgrid(-2:0.1:2,-4:0.1:2);
ZZ = objconstr([XX(:),YY(:)]).Ineq;
ZZ = reshape(ZZ,[size(XX),3]);
h = figure;
ax = gca;
contour(ax,XX,YY,ZZ(:,:,1),[-1/2 0],'r','ShowText','on');
hold on
contour(ax,XX,YY,ZZ(:,:,2),[-1/2 0],'k','ShowText','on');
contour(ax,XX,YY,ZZ(:,:,3),[-1/2 0],'b','ShowText','on');
hold off
end

次のコードは、補助関数 objconstr を作成します。

function f = objconstr(x)
c(:,1) = (x(:,2) + x(:,1).^2).^2 + 0.1*x(:,2).^2 - 1;
c(:,2) = x(:,2) - exp(-x(:,1)) + 3;
c(:,3) = x(:,2) - x(:,1) + 4;
f.Ineq = c;
end

次のコードは、補助関数 surrout を作成します。

function stop = surrout(~,optimValues,~)
stop = false;
if optimValues.constrviolation <= 1e-6 % Tolerance for constraint
    stop = true;
end
end

Copyright 2022–2024 The MathWorks, Inc.

参考

最適化 | fmincon | ga (Global Optimization Toolbox) | surrogateopt (Global Optimization Toolbox)

関連するトピック

• 非線形実行可能性問題の解法、問題ベース
• 線形実行不可能性の調査
• Solve Feasibility Problem (Global Optimization Toolbox)
• 問題ベースの最適化ワークフロー