このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

Clarke Transform

ab から αβ への変換の実装

• 

ライブラリ:
Motor Control Blockset / Controls / Math Transforms
Motor Control Blockset HDL Support / Controls / Math Transforms

説明

Clarke Transform ブロックは、abc 基準座標系における平衡三相成分の Clarke 変換を計算し、静止 αβ 基準座標系における平衡二相直交成分を出力します。あるいは、このブロックは三相成分 a、b、c の Clarke 変換を計算し、成分 α、β、0 を出力できます。平衡システムの場合、ゼロ成分はゼロに等しくなります。[入力数] パラメーターを使用して 2 つまたは 3 つの入力を使用します。

2 入力構成を使用する場合、ブロックは三相 (abc) から 2 つの信号を受け取り、3 番目の信号を自動的に計算して、αβ 基準座標系における対応する成分を出力します。

たとえば、a 相の軸が α 軸と揃っている場合、ブロックは入力値 a および b または多重化された入力値 abc を受け取ります。

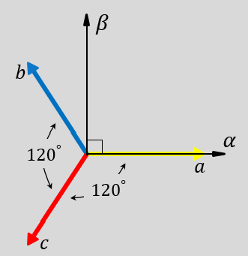
• 次の図は、abc 基準座標系と静止 αβ 基準座標系における固定子巻線の磁気軸の向きを示しています。

  

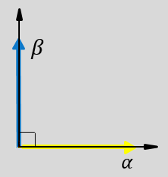
• 次の図は、静止 αβ 基準座標系における同等の α 成分と β 成分を示しています。

  

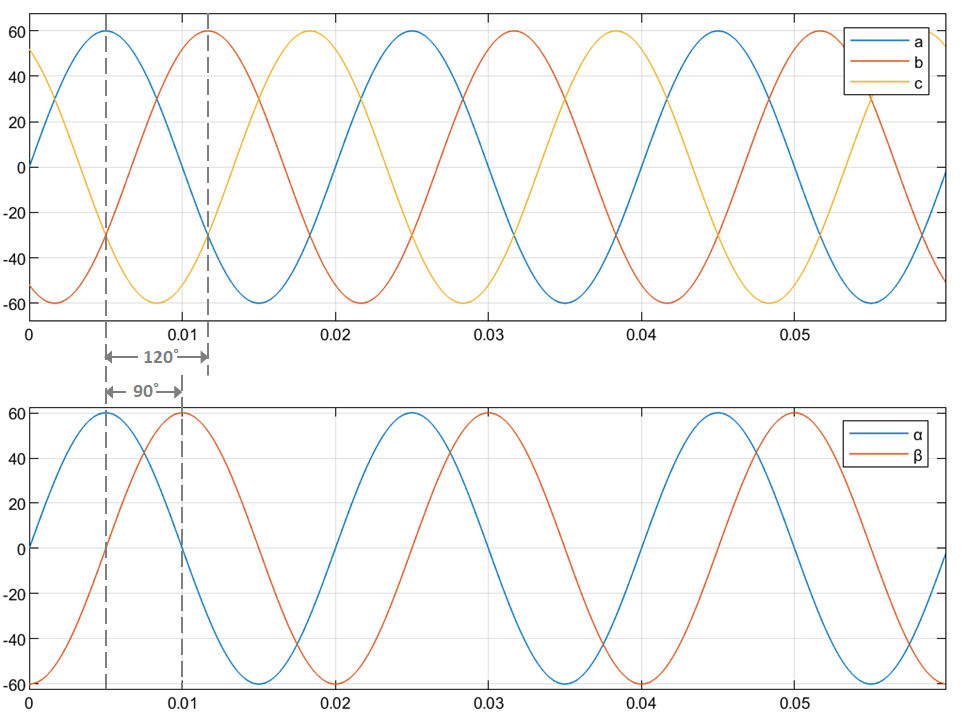
• 同等の平衡な abc システムと αβ システムの各成分の時間応答です。

  

方程式

Clarke 変換の計算は次の方程式で記述されます。

$\left[\begin{array}{c}{f}_{\alpha }\\ f_{\beta }\\ f_0\end{array}\right]=\left(\frac{2}{3}\right)\times \left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right]\left[\begin{array}{c}{f}_a\\ f_b\\ f_c\end{array}\right]$

モーターのような平衡システムの場合、ゼロ相成分の計算は常にゼロになります。たとえば、モーターの電流は次のように表すことができます。

$$i_a+i_b+i_c=0$$

したがって、三相モーター ドライブで使用できる電流センサーは 2 つだけです。ここで、3 番目の相は次のように計算できます。

$$i_c=-(i_a+i_b)$$

これらの方程式を使用して、このブロックは Clarke 変換を次のように実装します。

$\left[\begin{array}{c}{f}_{\alpha }\\ f_{\beta }\end{array}\right]=\left[\begin{array}{cc}1& 0\\ \frac{1}{\sqrt{3}}& \frac{2}{\sqrt{3}}\end{array}\right]\left[\begin{array}{c}{f}_a\\ f_b\end{array}\right]$

ここで以下のようになります。

• $f_a$、$f_b$、$f_c$ は、abc 基準座標系における平衡三相成分です。

• $f_{\alpha }$ と $f_{\beta }$ は、静止 αβ 基準座標系における平衡二相直交成分です。

• $f_0$ は、静止 αβ 基準座標系におけるゼロ成分です。

例

速度センサーを使用した誘導モーターのベクトル制御

この例では、三相交流誘導モーター (ACIM) の角速度を制御するためのベクトル制御 (FOC) 手法を実装します。この FOC アルゴリズムには回転子の速度フィードバックが必要であり、この例ではそれを直交エンコーダー センサーを使用して取得します。FOC の詳細については、ベクトル制御 (FOC)を参照してください。

• モデルを開く

ホール センサーを使用した PMSM のベクトル制御

この例では、三相永久磁石同期モーター (PMSM) の角速度を制御するためのベクトル制御 (FOC) 手法を実装します。この FOC アルゴリズムには回転子の位置フィードバックが必要であり、それをホール センサーで取得します。FOC の詳細については、ベクトル制御 (FOC)を参照してください。

• モデルを開く

端子

入力

a — 相成分

スカラー

abc 基準座標系における三相システムの成分。

依存関係

この端子を有効にするには、[入力数] パラメーターを [2 つの入力] に設定します。

データ型: single | double | fixed point

b — 相成分

スカラー

abc 基準座標系における三相システムの成分。

依存関係

この端子を有効にするには、[入力数] パラメーターを [2 つの入力] に設定します。

データ型: single | double | fixed point

abc — 相成分

スカラー

abc 基準座標系における三相システムの多重化された相成分 a、b、c。

依存関係

この端子を有効にするには、[入力数] パラメーターを [3 つの入力] に設定します。

データ型: single | double | fixed point

出力

α — 軸成分

スカラー

静止 αβ 基準座標系における alpha 軸成分 α。

依存関係

この端子を有効にするには、[入力数] パラメーターを [2 つの入力] に設定します。

データ型: single | double | fixed point

β — 軸成分

スカラー

静止 αβ 基準座標系における beta 軸成分 β。

依存関係

この端子を有効にするには、[入力数] パラメーターを [2 つの入力] に設定します。

データ型: single | double | fixed point

αβ0 — 軸成分

スカラー

静止 αβ 基準座標系における多重化された alpha 軸成分 α、beta 軸成分 β、および 0 成分。

依存関係

この端子を有効にするには、[入力数] パラメーターを [3 つの入力] に設定します。

データ型: single | double | fixed point

パラメーター

入力数 — ブロック入力の数

2 つの入力 (既定値) | 3 つの入力

指定できる入力の数を選択します。

• 2 つの入力 — 2 つの異なる入力信号 a および b を受け取るようにブロックを構成します。ブロックは 2 つの異なる出力信号 α および β を生成します。

• 3 つの入力 — a、b、c の各信号を含む多重化された入力を受け取るようにブロックを構成します。ブロックは α、β、0 の各信号を含む多重化された出力を生成します。

パワー不変 — パワー不変を有効にする

off (既定値) | on

ブロック出力のパワー不変プロパティを有効にするには、このパラメーターをオンにします。ブロック出力のパワー不変を無効にする (振幅不変を有効にする) には、このパラメーターをオフにします。

拡張機能

C/C++ コード生成
Simulink® Coder™ を使用して C および C++ コードを生成します。

HDL コード生成

HDL Coder™ を使用して FPGA 設計および ASIC 設計のための VHDL、Verilog および SystemVerilog のコードを生成します。

HDL Coder™ には、HDL の実装および合成されたロジックに影響する追加の構成オプションがあります。

HDL アーキテクチャ

このブロックには 1 つの既定の HDL アーキテクチャがあります。

HDL ブロック プロパティ

ConstrainedOutputPipeline	既存の遅延を設計内で移動することによって出力に配置するレジスタの数。分散型パイプラインではこれらのレジスタは再分散されません。既定の設定は 0 です。詳細については、ConstrainedOutputPipeline (HDL Coder)を参照してください。
InputPipeline	生成されたコードに挿入する入力パイプライン ステージ数。分散型パイプラインと制約付き出力パイプラインでは、これらのレジスタを移動できます。既定の設定は 0 です。詳細については、InputPipeline (HDL Coder)を参照してください。
OutputPipeline	生成されたコードに挿入する出力パイプライン ステージ数。分散型パイプラインと制約付き出力パイプラインでは、これらのレジスタを移動できます。既定の設定は 0 です。詳細については、OutputPipeline (HDL Coder)を参照してください。

固定小数点の変換
Fixed-Point Designer™ を使用して固定小数点システムの設計とシミュレーションを行います。

バージョン履歴

R2020a で導入

参考

Inverse Clarke Transform | Park Transform

トピック

• 開ループ制御と閉ループ制御
• ベクトル制御 (FOC)