ボロノイ線図
離散点 X の集合のボロノイ線図は、各点 X(i) のまわりで空間を領域 R{i} へ分解します。この分解は、R{i} 領域内にある任意の点 P が他の点よりも点 i に近い性質をもっています。影響範囲は、ボロノイ領域と呼ばれ、ボロノイ領域のすべての集合がボロノイ線図です。
ボロノイ線図は N 次元の幾何構成ですが、実際の用途は 2 次元および 3 次元空間であることがほとんどです。ボロノイ線図の性質は例を使うと理解が深まります。
2 次元ボロノイ線図と Delaunay 三角形分割のプロット
この例では、同じ 2 次元プロットにボロノイ線図と Delaunay 三角形分割を表します。
2-D の関数 voronoi を使用して、点集合のボロノイ線図をプロットします。
figure() X = [-1.5 3.2; 1.8 3.3; -3.7 1.5; -1.5 1.3; ... 0.8 1.2; 3.3 1.5; -4.0 -1.0;-2.3 -0.7; ... 0 -0.5; 2.0 -1.5; 3.7 -0.8; -3.5 -2.9; ... -0.9 -3.9; 2.0 -3.5; 3.5 -2.25]; voronoi(X(:,1),X(:,2)) % Assign labels to the points. nump = size(X,1); plabels = arrayfun(@(n) {sprintf('X%d', n)}, (1:nump)'); hold on Hpl = text(X(:,1), X(:,2), plabels, 'FontWeight', ... 'bold', 'HorizontalAlignment','center', ... 'BackgroundColor', 'none'); % Add a query point, P, at (0, -1.5). P = [0 -1]; plot(P(1),P(2), '*r'); text(P(1), P(2), 'P', 'FontWeight', 'bold', ... 'HorizontalAlignment','center', ... 'BackgroundColor', 'none'); hold off
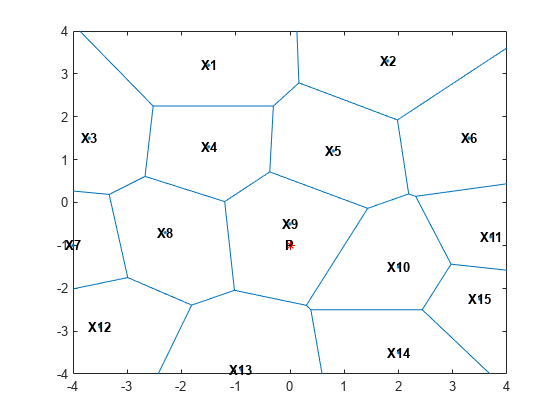
X9 の境界を示す領域内にある任意の点 P に対して true になる、X 内の P は他のどの点よりも X9 に近いことを確認します。
点集合 X のボロノイ線図は、X の Delaunay 三角形分割と密接に関連しています。この関係を見るには、点集合 X の Delaunay 三角形分割を作成し、ボロノイ線図に三角形分割プロットを重ね合わせます。
dt = delaunayTriangulation(X); hold on triplot(dt,'-r'); hold off
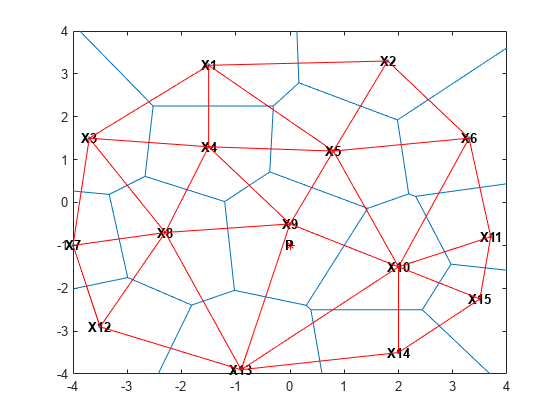
点 X9 と関連付けられるボロノイ領域は、X9 に接続された Delaunay エッジの垂直な二等分線で定義されることがプロットからわかります。また、ボロノイ エッジの頂点は、Delaunay 三角形の外心に配置されています。この関係は三角形 {|X9|,|X4|,|X8|} の外心をプロットすることで、示すことができます。
この三角形のインデックスを求めるには、三角形分割にクエリを行います。三角形は位置 (-1, 0) を含みます。
tidx = pointLocation(dt,-1,0);
ここで、この三角形の外心を求めて、それを緑色でプロットします。
cc = circumcenter(dt,tidx); hold on plot(cc(1),cc(2),'*g'); hold off

Delaunay 三角形分割とボロノイ線図はお互いに幾何双対です。ボロノイ線図を Delaunay 三角形分割から、またはその逆に計算できます。
凸包上の点と関連付けられるボロノイ領域は境界がありません (たとえば、X13 と関連付けられたボロノイ領域)。この領域のエッジは、無限で "終わります"。Delaunay エッジ (X13、X12) と (X13、X14) を二等分するボロノイ エッジは、無限に広がります。ボロノイ線図は、セットの各点の周りにある空間の最近傍分解を提供する一方、それは最近傍境界線を直接サポートしていません。ただし、ボロノイ線図を計算するために使用される幾何構造は、最近傍探索を実行するためにも使用されます。
ボロノイ線図の計算
この例では、2 次元および 3 次元ボロノイ線図を計算する方法を示します。
MATLAB® は、2 次元にボロノイ線図をプロットし、N 次元でのボロノイ線図のトポロジを計算するための関数を提供します。実際には、必要なメモリが指数関数的に増えるため、中規模から大規模のデータ セットの 6 次元を超える次元では、ボロノイ計算は実際的ではありません。
プロット関数 voronoi は、2 次元空間の点集合のボロノイ線図をプロットします。MATLAB では、点集合のボロノイ線図のトポロジを計算するため以下の 2 つの方法があります。
関数
voronoinを使用します。delaunayTriangulationメソッドvoronoiDiagramを使用します。
関数 voronoin は、N 次元 (N ≥ 2) の離散点に対するボロノイ線図のトポロジの計算をサポートします。voronoiDiagram メソッドは、2 次元または 3 次元の離散点に対するボロノイ線図のトポロジの計算をサポートします。
voronoiDiagram メソッドは、よりロバストであり、大規模なデータ セットに対してより優れた性能を発揮するので、2 次元または 3 次元のトポロジの計算に推奨されます。このメソッドは、インクリメンタルな挿入や点の削除、最近傍での点探索のような補完的探索要求をサポートしています。
関数 voronoin と voronoiDiagram メソッドは、行列形式を使用してボロノイ線図のトポロジを表します。このデータ構造体に関する詳細は、三角形分割の行列形式 を参照してください。
ボロノイ線図の計算
この例では、2 次元および 3 次元ボロノイ線図を計算する方法を示します。
与えられた点集合 X に対して、次のようにボロノイ線図のトポロジを取得します。
関数
voronoinを使用する
[V,R] = voronoin(X)
voronoiDiagramメソッドを使用する
dt = delaunayTriangulation(X);
[V,R] = voronoiDiagram(dt)
V はボロノイ頂点の座標を表す行列です (頂点はボロノイ エッジの終点です)。慣例により、V の最初の頂点は無限遠頂点になります。R は各点に関連するボロノイ領域を表す長さ size(X,1) のベクトル cell 配列です。したがって、点 X(i) に関連するボロノイ領域は R{i} です。
点集合のボロノイ線図を定義してプロットします。
X = [-1.5 3.2; 1.8 3.3; -3.7 1.5; -1.5 1.3; 0.8 1.2; ... 3.3 1.5; -4.0 -1.0; -2.3 -0.7; 0 -0.5; 2.0 -1.5; ... 3.7 -0.8; -3.5 -2.9; -0.9 -3.9; 2.0 -3.5; 3.5 -2.25]; [VX,VY] = voronoi(X(:,1),X(:,2)); h = plot(VX,VY,"-b",X(:,1),X(:,2),".r"); xlim([-4 4]) ylim([-4 4]) % Assign labels to the points X. nump = size(X,1); plabels = arrayfun(@(n) {sprintf('X%d', n)},(1:nump)'); hold on Hpl = text(X(:,1),X(:,2)+0.2,plabels,color="r",FontWeight="bold", ... HorizontalAlignment="center",BackgroundColor="none"); % Compute the Voronoi diagram. dt = delaunayTriangulation(X); [V,R] = voronoiDiagram(dt); % Assign labels to the Voronoi vertices V. % By convention the first vertex is at infinity. numv = size(V,1); vlabels = arrayfun(@(n) {sprintf("V%d", n)},(2:numv)'); hold on Hpl = text(V(2:end,1),V(2:end,2)+.2,vlabels,FontWeight="bold", ... HorizontalAlignment="center",BackgroundColor="none"); hold off
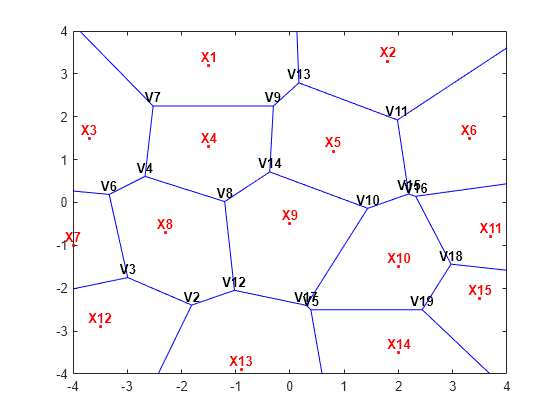
R{9} により、点の位置 X9 に関連するボロノイ頂点のインデックスが得られます。
R{9}ans = 1×5
8 12 17 10 14
ボロノイ頂点のインデックスは配列 V を基準とするインデックスです。
同様に、R{4} により、点の位置 X4 に関連するボロノイ頂点のインデックスが得られます。
R{4}ans = 1×5
4 8 14 9 7
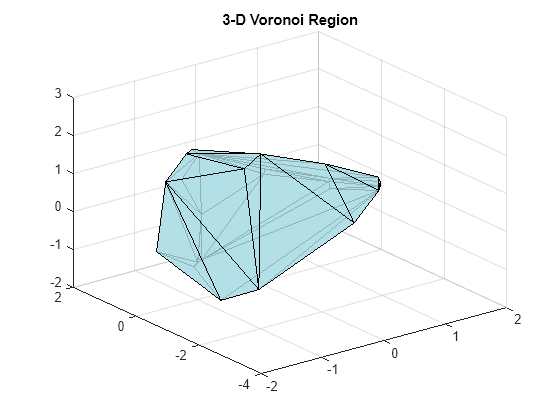
3 次元の場合、ボロノイ領域は凸多面体になります。ボロノイ線図を作成するための構文は類似しています。ただし、ボロノイ領域の形状がより複雑になります。次の例では、3 次元ボロノイ線図を作成し、単一の領域をプロットします。
3 次元空間の 25 個の点からなるサンプルを作成し、この点集合に対するボロノイ線図のトポロジを計算します。
rng("default")
X = -3 + 6.*rand([25 3]);
dt = delaunayTriangulation(X);ボロノイ線図のトポロジを計算します。
[V,R] = voronoiDiagram(dt);
原点に最も近い点を調べ、この点に関連するボロノイ領域をプロットします。
tid = nearestNeighbor(dt,0,0,0);
XR10 = V(R{tid},:);
K = convhull(XR10);
defaultFaceColor = [0.6875 0.8750 0.8984];
trisurf(K,XR10(:,1),XR10(:,2),XR10(:,3) , ...
FaceColor=defaultFaceColor,FaceAlpha=0.8)
title("3-D Voronoi Region")