基本的なスペクトル解析
フーリエ変換は、時間領域信号の周波数およびパワー スペクトルの解析を行うためのツールです。
スペクトル解析の量
スペクトル解析では、離散型の、等間隔でサンプリングされたデータに含まれる周波数スペクトルを調べます。フーリエ変換は、時間または空間ベースの信号を周波数空間で表すことによって、その周波数成分を明らかにするツールです。以下の表は、信号のプロパティの特徴付けや解釈に使用する一般的な量を示しています。フーリエ変換の詳細については、フーリエ変換を参照してください。
| 量 | 説明 |
|---|---|
x | サンプル データ |
n = length(x) | サンプル数 |
fs | サンプル周波数 (単位時間または単位空間ごとのサンプル) |
dt = 1/fs | サンプルごとの時間または空間のインクリメント |
t = (0:n-1)/fs | データの時間範囲または空間範囲 |
y = fft(x) | データの離散フーリエ変換 (DFT) |
abs(y) | DFT の振幅 |
(abs(y).^2)/n | DFT のパワー |
fs/n | 周波数分解能 |
f = (0:n-1)*(fs/n) | 周波数範囲 |
fs/2 | ナイキスト周波数 (周波数範囲の中間点) |
ノイズを含む信号
フーリエ変換では、ランダム ノイズによって破損した信号の周波数成分を計算できます。
周波数成分が 15 Hz と 40 Hz の信号を作成し、ランダムなガウス ノイズを投入します。
rng('default') fs = 100; % sample frequency (Hz) t = 0:1/fs:10-1/fs; % 10 second span time vector x = (1.3)*sin(2*pi*15*t) ... % 15 Hz component + (1.7)*sin(2*pi*40*(t-2)) ... % 40 Hz component + 2.5*randn(size(t)); % Gaussian noise;
信号のフーリエ変換により、周波数成分が特定されます。MATLAB® では、高速フーリエ変換アルゴリズムを使用して関数fftによりフーリエ変換が計算されます。fft を使用して、信号の離散フーリエ変換を計算します。
y = fft(x);
パワー スペクトルを、周波数の関数としてプロットします。時間ベースの空間では信号の周波数成分がノイズによって隠されますが、フーリエ変換により、パワーのスパイクとして明示されます。
n = length(x); % number of samples f = (0:n-1)*(fs/n); % frequency range power = abs(y).^2/n; % power of the DFT plot(f,power) xlabel('Frequency') ylabel('Power')
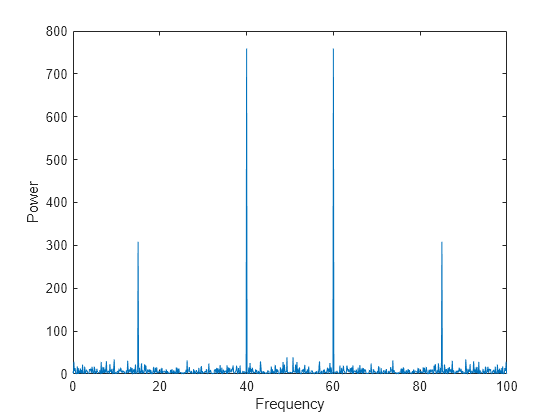
多くのアプリケーションでは、周波数 0 を中央にしてパワー スペクトルを表示したほうが、信号の周期性をよく表現できて便利です。関数fftshiftを使用して y で循環シフトを実行し、0 を中央にしたパワーをプロットします。
y0 = fftshift(y); % shift y values f0 = (-n/2:n/2-1)*(fs/n); % 0-centered frequency range power0 = abs(y0).^2/n; % 0-centered power plot(f0,power0) xlabel('Frequency') ylabel('Power')
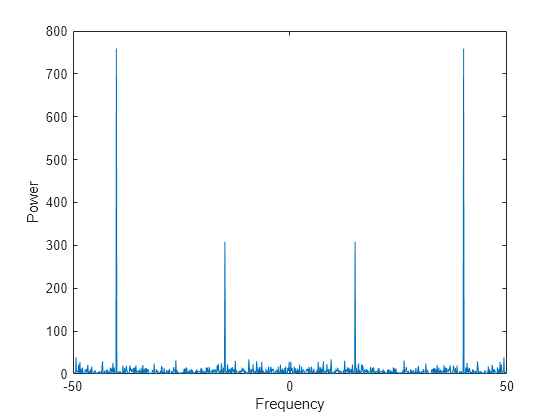
オーディオ信号
フーリエ変換を使用して、オーディオ データの周波数スペクトルを解析できます。
ファイル bluewhale.au には、カリフォルニア沿岸沖で水中マイクによって記録された太平洋のシロナガスクジラの鳴き声のオーディオ データが収録されています。このファイルは、Cornell University Bioacoustics Research Program で保管されている動物の鳴き声のライブラリから入手したものです。
シロナガスクジラの鳴き声は非常に低いため、人間はほとんど聞き取れません。データの時間スケールは、音程を上げて鳴き声がよりはっきりと聞こえるように 10 倍に圧縮されています。オーディオ データを読み取ってプロットします。コマンド sound(x,fs) を使用してオーディオを聴くことができます。
whaleFile = 'bluewhale.au'; [x,fs] = audioread(whaleFile); plot(x) xlabel('Sample Number') ylabel('Amplitude')
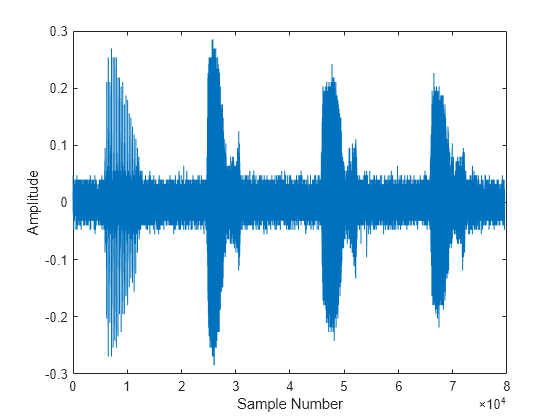
最初の音声は "震え音" で、その後に "うめき声" が 3 回続きます。この例では、1 回のうめき声を解析します。最初のうめき声が概ね含まれるように新しいデータを指定し、10 倍にスピードアップすることを考慮して時間データを修正します。切り取った信号を時間の関数としてプロットします。
moan = x(2.45e4:3.10e4); t = 10*(0:1/fs:(length(moan)-1)/fs); plot(t,moan) xlabel('Time (seconds)') ylabel('Amplitude') xlim([0 t(end)])

データのフーリエ変換により、オーディオ信号の周波数成分が特定されます。fft を使って大量のデータを処理するアプリケーションでは、サンプルの数が 2 のべき乗になるように入力のサイズを変更するのが一般的です。これにより、特にサンプル サイズに大きな素因数が含まれている場合に、変換の計算が大幅に速くなります。2 のべき乗である新しい信号長 n を指定し、関数 fft を使用して信号の離散フーリエ変換を計算します。fft では、サンプル サイズを拡大するために、元のデータにゼロが自動的に付加されます。
m = length(moan); % original sample length n = pow2(nextpow2(m)); % transform length y = fft(moan,n); % DFT of signal
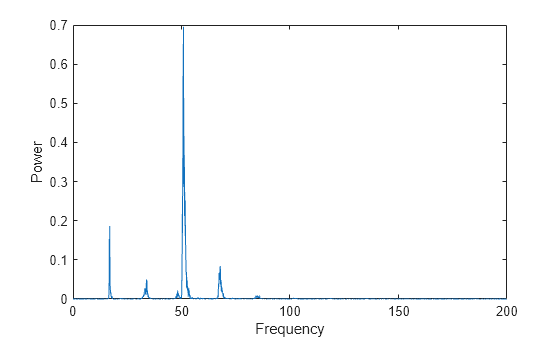
スピードアップの係数に応じて周波数範囲を調整し、信号のパワー スペクトルを計算してプロットします。プロットは、うめき声が 17 Hz 前後の基本周波数と、2 番目の調波が強い高調波群から構成されていることを示しています。
f = (0:n-1)*(fs/n)/10; power = abs(y).^2/n; plot(f(1:floor(n/2)),power(1:floor(n/2))) xlabel('Frequency') ylabel('Power')
参考
fft | fftshift | nextpow2 | ifft | fft2 | fftn