配列インデックス付け
MATLAB® では、配列の場所 (インデックス) に基づいて配列要素にアクセスする方法が主に 3 つあります。これらの方法は、位置によるインデックス付け、線形インデックス付け、論理インデックス付けです。位置によるインデックス付けと論理インデックス付けの両方を組み合わせて、混合インデックス付けを使用することもできます。
要素の位置によるインデックス付け
最も一般的な手法は、要素のインデックスを明示的に指定することです。たとえば、行列の 1 つの要素にアクセスするには、行番号に続けて要素の列番号を指定します。
A = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]
A = 4×4
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
e = A(3,2)
e = 10
e は A の 3,2 位置 (3 行目、2 列目) の要素です。
ベクトルで該当するインデックスを指定することで、複数の要素を一度に参照することもできます。たとえば、A の 2 行目の最初と 3 番目の要素にアクセスします。
r = A(2,[1 3])
r = 1×2
5 7
行または列の範囲内の要素にアクセスするには、colon演算子を使用します。たとえば、A の最初の行から 3 行目および 2 列目から 4 列目までの要素にアクセスします。
r = A(1:3,2:4)
r = 3×3
2 3 4
6 7 8
10 11 12
これらの要素にアクセスする別の方法は、キーワード end を使用して最後の列を表すことです。この方法では、A にある正確な列数がわからなくても、最後の列を指定できます。
r = A(1:3,2:end)
r = 3×3
2 3 4
6 7 8
10 11 12
すべての行と列にアクセスするには、それ自体でコロン演算子を使用します。たとえば、A の 3 番目の行全体を返します。
r = A(3,:)
r = 1×4
9 10 11 12
コロン演算子と end キーワードを使用して、A の最後から 2 番目の列にアクセスすることもできます。
r = A(:,end-1)
r = 4×1
3
7
11
15
一般に、データ型または次元に関係なく、インデックス付けを使用して MATLAB で任意の配列の要素にアクセスできます。たとえば、datetimeの配列の列に直接アクセスします。
t = [datetime(2018,1:5,1); datetime(2019,1:5,1)]
t = 2×5 datetime
01-Jan-2018 01-Feb-2018 01-Mar-2018 01-Apr-2018 01-May-2018
01-Jan-2019 01-Feb-2019 01-Mar-2019 01-Apr-2019 01-May-2019
march1 = t(:,3)
march1 = 2×1 datetime
01-Mar-2018
01-Mar-2019
高次元の配列の場合、配列の次元に一致するように構文を拡張します。ランダムな 3 x 3 x 3 の数値配列を考えます。配列の 2 番目の行、3 番目の列、および最初のシートの要素にアクセスします。
A = rand(3,3,3); e = A(2,3,1)
e = 0.5469
多次元配列での処理の詳細については、多次元配列を参照してください。
単一のインデックスによるインデックス付け
配列の要素にアクセスする別の手法は、配列のサイズまたは次元に関係なく、単一のインデックスのみを使用することです。この手法は、"線形インデックス付け" と呼ばれています。MATLAB は、定義されたサイズおよび形状に従った配列を表示しますが、これらは実際、左から右へと行われ、列単位でメモリに格納されます。この概念を可視化する優れた方法は、行列を使用することです。次の配列は 3 行 3 列の行列として表示されますが、MATLAB はこれを、A の列が次々連結されて構成される単一の列として格納します。格納されたベクトルには、要素 12、45、33、36、29、25、91、48、11 のシーケンスが含まれ、単一のコロンを使用して表示できます。
A = [12 36 91; 45 29 48; 33 25 11]
A = 3×3
12 36 91
45 29 48
33 25 11
Alinear = A(:)
Alinear = 9×1
12
45
33
36
29
25
91
48
11
たとえば、A の 3,2 要素は 25 であり、構文 A(3,2) を使用してアクセスできます。この要素は、構文 A(6) を使用してアクセスすることもできます。これは、格納されたベクトル シーケンスで 25 が 6 番目の要素であるためです。
e = A(3,2)
e = 25
elinear = A(6)
elinear = 25
線形インデックス付けは視覚的にあまり直観的ではありませんが、配列のサイズまたは形状に依存しない特定の計算を実行する場合に効果的です。たとえば、関数 sum に 2 番目の引数を指定しなくても、A のすべての要素を簡単に加算できます。
s = sum(A(:))
s = 330
関数 sub2ind と関数 ind2sub を使用して、元の配列インデックスとその線形バージョン間で変換できます。たとえば、A の 3,2 要素の線形インデックスを計算します。
linearidx = sub2ind(size(A),3,2)
linearidx = 6
線形インデックスを、その行と列の形式に変換し直します。
[row,col] = ind2sub(size(A),6)
row = 3
col = 2
論理値によるインデックス付け
true と false の論理インジケーターの使用は、条件付きステートメントを処理する場合は特に、配列にインデックス付けする別の便利な手法です。たとえば、行列 A の要素が別の行列 B の対応する要素よりも小さいかどうかを確認するとします。less-than 演算子は、A の要素が B の対応する要素よりも小さい場合に要素が 1 である logical 配列を返します。
A = [1 2 6; 4 3 6]
A = 2×3
1 2 6
4 3 6
B = [0 3 7; 3 7 5]
B = 2×3
0 3 7
3 7 5
ind = A < B
ind = 2×3 logical array
0 1 1
0 1 0
これで、条件を満たす要素の位置がわかり、ind をインデックス配列として使用して個々の値を検査できます。MATLAB は、ind の値 1 の位置と A および B の対応する要素の位置を照合し、それらの値を列ベクトルにリストします。
Avals = A(ind)
Avals = 3×1
2
3
6
Bvals = B(ind)
Bvals = 3×1
3
7
7
また MATLAB 関数 "is" は、入力のどの要素が特定の条件を満たすかを示す logical 配列を返します。たとえば、ismissing関数を使用して、string ベクトルの欠落している要素を確認します。
str = ["A" "B" missing "D" "E" missing]; ind = ismissing(str)
ind = 1×6 logical array
0 0 1 0 0 1
欠落して "いない" 要素の値を検索するとします。これを行うには、インデックス ベクトル ind で ~ 演算子を使用します。
strvals = str(~ind)
strvals = 1×4 string
"A" "B" "D" "E"
論理インデックス付けを使用する例の詳細については、条件を満たす配列要素の検索を参照してください。
論理値と要素の位置による混合インデックス付け
位置によるインデックス付けと論理インデックス付けを組み合わせて使用して、配列要素にアクセスすることもできます。
たとえば、5 行 5 列の行列を作成します。
A = magic(5)
A = 5×5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
行のインデックスが素数で、列のインデックスが 2、3、および 4 である A の要素を選択するとします。
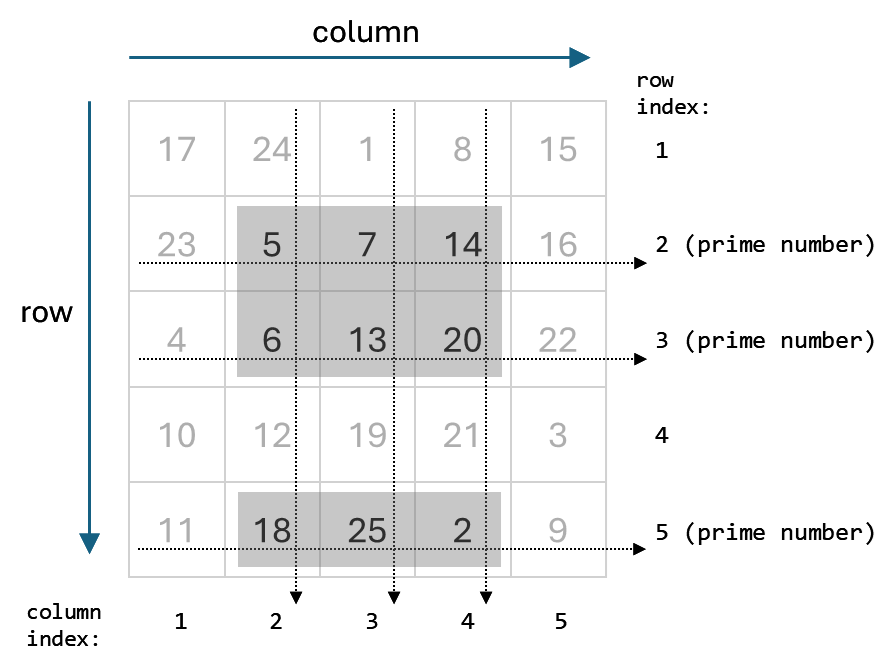
これを行うには、A の行のインデックスを表すベクトル B を作成します。
B = (1:size(A,1))
B = 1×5
1 2 3 4 5
isprime 関数を使用して、B のどの要素が素数であるかを判別します。結果は、A の行にインデックスを付けるために使用できる logical 配列です。
rows = isprime(B)
rows = 1×5 logical array
0 1 1 0 1
次に、選択する列 (位置 2 から 4) を定義します。
cols = 2:4
cols = 1×3
2 3 4
論理インデックス付けを使用して、rows で定義されているように、素数の位置にある A の行を選択します。次に、位置によるインデックス付けを使用して、cols で定義されているように、位置 2 から 4 までの範囲の A の列を選択します。
A(rows,cols)
ans = 3×3
5 7 14
6 13 20
18 25 2
参考
トピック
- categorical 配列によるデータへのアクセス
- table 内のデータへのアクセス
- 構造体配列
- cell 配列のデータへのアクセス
- インデックス付き代入
- Detailed Rules for Array Indexing