integralImage
2 次元積分イメージの計算
説明
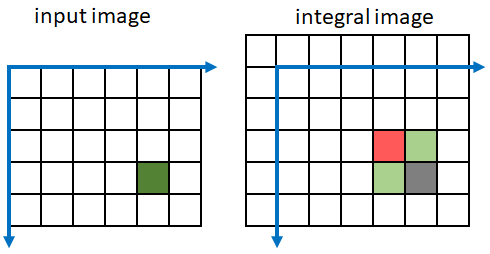
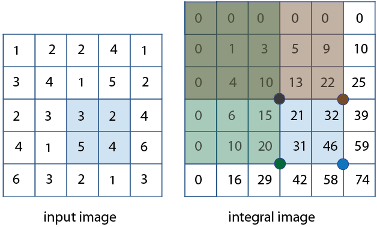
"積分イメージ" の各ピクセルは、対応する入力ピクセルとその入力ピクセルの上側および左側のすべてのピクセルの累積和を表します。
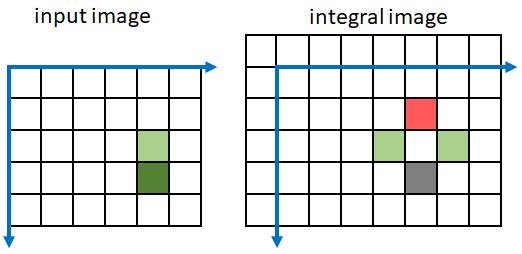
積分イメージを使用すると、イメージの部分領域の総和を高速に計算できます。部分領域の総和は、部分領域のサイズに関係なく、積分イメージ内の 4 つのピクセルのみの線形結合として定数時間で計算できます。積分イメージの使用は Viola-Jones アルゴリズムによって一般に普及しました[1]。
例
簡単なサンプル行列を作成します。
I = magic(5)
I = 5×5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
サンプル行列の積分イメージを計算します。以下の手順は、元の行列の最初のいくつかの値が積分イメージの値にどのようにマッピングされるかを示すものです。元のイメージにある (行, 列) 座標が (r, c) のピクセルは、積分イメージの座標 (r+1, c+1) のピクセルに対応することに注意してください。
積分イメージの最初の行と列はすべて
0です。元の行列の座標 (1, 1) にある、値が 17 のピクセルは、和の中に他のピクセルがないため積分イメージ内で変化しません。そのため、積分イメージの座標 (2, 2) のピクセルは値が 17 になります。
元の行列の座標 (1, 2) のピクセルは積分イメージのピクセル (2, 3) にマッピングされます。その値は、元のピクセル値 (24)、その上側のピクセル (0)、左側のピクセル (17) の総和であり、次のようになります。24 + 17 + 0 = 41.
元の行列の座標 (1, 3) のピクセルは積分イメージのピクセル (2, 4) にマッピングされます。その値は、元のピクセル値 (1)、その上側のピクセル (0)、左側のピクセル (既に合計済みで 41) の総和です。したがって、積分イメージのピクセル (2, 4) の値は 1 + 41 + 0 = 42 になります。
J = integralImage(I)
J = 6×6
0 0 0 0 0 0
0 17 41 42 50 65
0 40 69 77 99 130
0 44 79 100 142 195
0 54 101 141 204 260
0 65 130 195 260 325
グレースケール イメージをワークスペースに読み取ります。イメージを表示します。
I = imread('pout.tif');
imshow(I)
積分イメージを計算します。
J = integralImage(I);
drawrectangle ツールを使用して四角形の部分領域を選択します。ツールは Rectangle オブジェクトを返します。
d = drawrectangle;
Rectangle オブジェクトの Vertices プロパティは、4 行 2 列の行列として頂点の座標を格納します。頂点は、左上から開始して時計回りの方向に続く順番で並べられます。行座標と列座標を含む 2 つのベクトルに行列を分割します。積分イメージは上側と左側でゼロ パディングされているため、行座標と列座標を 1 増やして積分配列の対応要素を取得します。
r = floor(d.Vertices(:,2)) + 1; c = floor(d.Vertices(:,1)) + 1;
積分イメージの 4 つのピクセルを結合することにより、四角形の部分領域にあるすべてのピクセルの和を計算します。
regionSum = J(r(1),c(1)) - J(r(2),c(2)) + J(r(3),c(3)) - J(r(4),c(4))
regionSum = 613092
簡単なサンプル行列を作成します。
I = magic(5)
I = 5×5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
回転した方向の積分イメージを作成します。
J = integralImage(I,'rotated')J = 6×7
0 0 0 0 0 0 0
0 17 24 1 8 15 0
17 64 47 40 38 39 15
64 74 91 104 105 76 39
74 105 149 188 183 130 76
105 170 232 272 236 195 130
回転した四角形の部分領域を定義します。この例では、元のイメージの座標 (1,3) に上側の隅がある部分領域を指定します。部分領域の回転した高さは 1 で幅は 2 です。
r = 1; c = 3; h = 1; w = 2;
積分イメージ内の部分領域の 4 つの隅にあるピクセルの値を取得します。
regionBottom = J(r+w+h,c-h+w+1); regionTop = J(r,c+1); regionLeft = J(r+h,c-h+1); regionRight = J(r+w,c+w+1); regionCorners = [regionBottom regionTop regionLeft regionRight]
regionCorners = 1×4
105 0 24 39
4 つの隅のピクセル値を合計することにより、部分領域のピクセルの和を計算します。
regionSum = regionBottom + regionTop - regionLeft - regionRight
regionSum = 42
入力引数
出力引数
アルゴリズム
積分イメージのどのピクセルも、対応する入力ピクセル値とその入力ピクセルの上側および左側のすべての入力ピクセルの総和を表します。integralImage は結果として得られる積分イメージをゼロ パディングするため、元のイメージにある (行, 列) 座標が (m, n) のピクセルは、積分イメージの座標 (m+1, n+1) のピクセルにマッピングされます。
図の中で、入力イメージの現在のピクセルは、座標 (4, 5) の濃い緑色のピクセルです。入力ピクセルの上側および左側にある入力イメージのすべてのピクセルを薄い緑色で示してあります。緑色のピクセル値の総和は、積分イメージの座標 (5, 6) にある灰色で示したピクセルに返されます。
integralImage は、入力イメージと積分イメージの両方のピクセル値を合計することによって、積分イメージを高速に計算します。積分イメージ J のピクセル (m, n) は、4 つのピクセルのみの線形結合です。1 つは入力イメージのピクセル、3 つは前に計算した積分イメージのピクセルです。
J(m,n) = J(m,n-1) + J(m-1,n) + I(m-1,n-1) - J(m-1,n-1)
この図は、灰色ピクセルの積分イメージを計算するときに、どのピクセルが和に含まれているかを示しています。緑色のピクセルは和に加算され、赤色のピクセルは和から減算されます。
イメージ orientation を "rotated" として指定した場合、積分イメージのピクセルは、対応する入力ピクセル値と、その入力ピクセルを通る斜め上方向の線上とその線の上側にあるすべての入力ピクセルの総和を表します。integralImage は、その斜め上方向の線に基づいて総和を実行します。この手法は、イメージを回転して直角方向に積分イメージを計算するよりも、計算負荷が少なくなります。
図の中で、入力イメージの現在のピクセルは、座標 (4, 5) の濃い緑色のピクセルです。入力ピクセルを通る斜め上方向の線上とその線の上側にある入力イメージのすべてのピクセルを薄い緑色で示してあります。緑色のピクセル値の総和は、積分イメージの座標 (5, 6) にある灰色で示したピクセルに返されます。
integralImage は、入力イメージと積分イメージの両方のピクセル値を合計することによって、回転した積分イメージを高速に計算します。積分イメージ J のピクセル (m, n) は、5 つのピクセルのみの線形結合です。2 つは入力イメージのピクセル、3 つは前に計算した積分イメージのピクセルです。
J(m,n) = J(m-1,n-1) + J(m-1,n+1) - J(m-2,n) + I(m-1,n-1) + I(m-2,n-1)
この図は、灰色ピクセルの積分イメージを計算するときに、どのピクセルが和に含まれているかを示しています。緑色のピクセルは和に加算され、赤色のピクセルは和から減算されます。
元のイメージで、左上の座標 (m,n)、高さ h、および幅 w をもつ垂直方向の部分領域の和は、
regionSum = J(m–1,n–1) + J(m+h–1,n+w–1) – J(m+h–1,n–1) – J(m-1,n+w-1)
となります。
たとえば、下の入力イメージで、青色の影付き領域の和は、次のようになります。46 – 22 – 20 + 10 = 14.計算では影付き領域の上側と左側の領域を減算しています。減算の重複を補正するために、重なった部分を加算し直しています。
回転した方向の部分領域では、異なる定義の高さと幅を使用します [2]。領域の和は次のようになります。
regionSum = J(m+h+w,n-h+w+1) + J(m,n+1) - J(m+h,n-h+1) - J(m+w,n+w+1)
参照
[1] Viola, P., and M. J. Jones. "Rapid Object Detection using a Boosted Cascade of Simple Features". Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2001. Vol. 1, pp. 511–518.
[2] Lienhart, R., and J. Maydt. "An Extended Set of Haar-like Features for Rapid Object Detection". Proceedings of the 2002 IEEE International Conference on Image Processing. Sept. 2002. Vol. 1, pp. 900–903.
