GPU Coder を使用した線形システム求解のベンチマーク

ライブスクリプトを開く

この例では、CUDA® コードを生成することによって、線形システム求解のベンチマークを行う方法を示します。行列の左除算 (mldivideまたはバックスラッシュ演算子 (\) とも呼ばれる) を使用して、連立線形方程式 A*x = b を x について解きます (つまり、x = A\b を計算します)。

サードパーティの前提条件

必要

この例では、CUDA MEX を生成します。以下のサードパーティ要件が適用されます。

CUDA 対応 NVIDIA® GPU および互換性のあるドライバー。

オプション

スタティックライブラリ、ダイナミックライブラリ、または実行可能ファイルなどの MEX 以外のビルドについて、この例では以下の要件も適用されます。

NVIDIA Toolkit。
コンパイラおよびライブラリの環境変数。詳細については、サードパーティハードウェアと前提条件となる製品の設定を参照してください。

GPU 環境の検証

この例を実行するのに必要なコンパイラおよびライブラリが正しく設定されていることを検証するために、関数coder.checkGpuInstallを使用します。

envCfg = coder.gpuEnvConfig('host');
envCfg.BasicCodegen = 1;
envCfg.Quiet = 1;
coder.checkGpuInstall(envCfg);

最大データサイズの決定

CPU および GPU で利用できるシステムメモリの量を GB 単位で指定して、計算に適切な行列のサイズを選択します。既定値は GPU で利用できるメモリの量のみに基づきます。システムに適切な値を指定することができます。

g = gpuDevice; 
maxMemory = 0.1*g.AvailableMemory/1024^3;

メモ:

この例では、ワークスペースを作成するために大容量の GPU メモリを必要とする cuSOLVER ライブラリを使用します。CUDA のメモリ不足エラーが発生した場合は、maxMemory を減らすか、sizeSingle と sizeDouble の行列のステップサイズを減らしてください。

ベンチマーク関数

この例では、CPU と GPU の間でのデータ転送コストを含む、GPU Coder™ 使用時の全体的なアプリケーションの時間を明確に把握するために、行列の左除算 (\) のベンチマークを実行します。アプリケーション時間のプロファイリングには、サンプル入力データを作成するための時間を含めてはなりません。getData.m 関数は、線形システムを解くエントリポイント関数とは別にテストデータを生成します。

type getData.m

function [A, b] = getData(n, clz)

%   Copyright 2017-2022 The MathWorks, Inc.

    fprintf('Creating a matrix of size %d-by-%d.\n', n, n);
    A = rand(n, n, clz) + 100*eye(n, n, clz);
    b = rand(n, 1, clz);
end

バックスラッシュエントリポイント関数

backslash.m エントリポイント関数は、コードを生成する (\) 演算をカプセル化します。

type backslash.m

function [x] = backslash(A,b)
%#codegen

%   Copyright 2017-2022 The MathWorks, Inc.

    coder.gpu.kernelfun();
    x = A\b;
end

GPU コードの生成

特定の入力データサイズに基づいて GPU MEX 関数を生成する関数を作成します。

type genGpuCode.m

function [] = genGpuCode(A, b)

%   Copyright 2017-2022 The MathWorks, Inc.

    cfg = coder.gpuConfig('mex');
    evalc('codegen -config cfg -args {A,b} backslash');
end

問題サイズの選択

線形システムを解く並列アルゴリズムのパフォーマンスは、行列のサイズに大きく左右されます。この例では、さまざまな行列のサイズ (1024 の倍数) についてアルゴリズムのパフォーマンスを比較します。

sizeLimit = inf;
if ispc
    sizeLimit = double(intmax('int32'));
end
maxSizeSingle = min(floor(sqrt(maxMemory*1024^3/4)),floor(sqrt(sizeLimit/4)));
maxSizeDouble = min(floor(sqrt(maxMemory*1024^3/8)),floor(sqrt(sizeLimit/8)));
step = 1024;
if maxSizeDouble/step >= 10
    step = step*floor(maxSizeDouble/(5*step));
end
sizeSingle = 1024:step:maxSizeSingle;
sizeDouble = 1024:step:maxSizeDouble;
numReps = 5;

パフォーマンスの比較: 高速化

合計経過時間をパフォーマンスの測定基準として使用します。そうすることで、さまざまな行列のサイズについてアルゴリズムのパフォーマンスを比較できるためです。行列のサイズを与えると、ベンチマーク関数は行列 A と右辺 b を 1 回作成し、A\b を数回解くことでそれに要した正確な時間を測定します。

type benchFcnMat.m

function time = benchFcnMat(A, b, reps)

%   Copyright 2017-2022 The MathWorks, Inc.

    time = inf;
    % Solve the linear system a few times and take the best run
    for itr = 1:reps
        tic;
        matX = backslash(A, b);
        tcurr = toc;
        time = min(tcurr, time);
    end
end

生成された GPU MEX 関数を呼び出す GPU コード実行用の別の関数を作成します。

type benchFcnepu.m

function time = benchFcnGpu(A, b, reps)

%   Copyright 2017-2022 The MathWorks, Inc.

    time = inf;
    gpuX = backslash_mex(A, b);
    for itr = 1:reps
        tic;
        gpuX = backslash_mex(A, b);
        tcurr = toc;
        time = min(tcurr, time);
    end
end

ベンチマークの実行

ベンチマークを実行する場合、計算が完了するまでに長い時間がかかる可能性があります。各行列のサイズについてのベンチマークの完了時に、一部の中間ステータス情報を出力します。単精度および倍精度の計算についてベンチマークを実行するために、すべての行列のサイズに対するループを関数にカプセル化します。

実際の実行時間はハードウェア構成によって異なる可能性があります。このベンチマークは、6 コアの 3.5 GHz Intel® Xeon® CPU および NVIDIA TITAN Xp GPU を搭載したマシンで MATLAB R2022a を使用して行われました。

type executeBenchmarks.m

function [timeCPU, timeGPU] = executeBenchmarks(clz, sizes, reps)

%   Copyright 2017-2022 The MathWorks, Inc.

    fprintf(['Starting benchmarks with %d different %s-precision ' ...
         'matrices of sizes\nranging from %d-by-%d to %d-by-%d.\n'], ...
            length(sizes), clz, sizes(1), sizes(1), sizes(end), ...
            sizes(end));
    timeGPU = zeros(size(sizes));
    timeCPU = zeros(size(sizes));   
    for i = 1:length(sizes)
        n = sizes(i);
        fprintf('Size : %d\n', n);
        [A, b] = getData(n, clz);
        genGpuCode(A, b);
        timeCPU(i) = benchFcnMat(A, b, reps);
        fprintf('Time on CPU: %f sec\n', timeCPU(i));
        timeGPU(i) = benchFcnGpu(A, b, reps);
        fprintf('Time on GPU: %f sec\n', timeGPU(i));
        fprintf('\n');
    end
end

単精度および倍精度でベンチマークを実行します。

[cpu, gpu] = executeBenchmarks('single', sizeSingle, numReps);

Starting benchmarks with 8 different single-precision matrices of sizes
ranging from 1024-by-1024 to 22528-by-22528.
Size : 1024
Creating a matrix of size 1024-by-1024.
Time on CPU: 0.011866 sec
Time on GPU: 0.004042 sec

Size : 4096
Creating a matrix of size 4096-by-4096.
Time on CPU: 0.246468 sec
Time on GPU: 0.023765 sec

Size : 7168
Creating a matrix of size 7168-by-7168.
Time on CPU: 0.897369 sec
Time on GPU: 0.064114 sec

Size : 10240
Creating a matrix of size 10240-by-10240.
Time on CPU: 2.199820 sec
Time on GPU: 0.138756 sec

Size : 13312
Creating a matrix of size 13312-by-13312.
Time on CPU: 4.589138 sec
Time on GPU: 0.253298 sec

Size : 16384
Creating a matrix of size 16384-by-16384.
Time on CPU: 8.026105 sec
Time on GPU: 0.418530 sec

Size : 19456
Creating a matrix of size 19456-by-19456.
Time on CPU: 12.909238 sec
Time on GPU: 0.640920 sec

Size : 22528
Creating a matrix of size 22528-by-22528.
Time on CPU: 19.308684 sec
Time on GPU: 0.935741 sec

results.sizeSingle = sizeSingle;
results.timeSingleCPU = cpu;
results.timeSingleGPU = gpu;
[cpu, gpu] = executeBenchmarks('double', sizeDouble, numReps);

Starting benchmarks with 6 different double-precision matrices of sizes
ranging from 1024-by-1024 to 16384-by-16384.
Size : 1024
Creating a matrix of size 1024-by-1024.
Time on CPU: 0.024293 sec
Time on GPU: 0.010438 sec

Size : 4096
Creating a matrix of size 4096-by-4096.
Time on CPU: 0.431786 sec
Time on GPU: 0.129416 sec

Size : 7168
Creating a matrix of size 7168-by-7168.
Time on CPU: 1.684876 sec
Time on GPU: 0.559612 sec

Size : 10240
Creating a matrix of size 10240-by-10240.
Time on CPU: 4.476006 sec
Time on GPU: 1.505087 sec

Size : 13312
Creating a matrix of size 13312-by-13312.
Time on CPU: 8.845687 sec
Time on GPU: 3.188244 sec

Size : 16384
Creating a matrix of size 16384-by-16384.
Time on CPU: 17.680626 sec
Time on GPU: 5.831711 sec

results.sizeDouble = sizeDouble;
results.timeDoubleCPU = cpu;
results.timeDoubleGPU = gpu;

パフォーマンスのプロット

結果をプロットし、単精度および倍精度についての CPU および GPU のパフォーマンスを比較します。

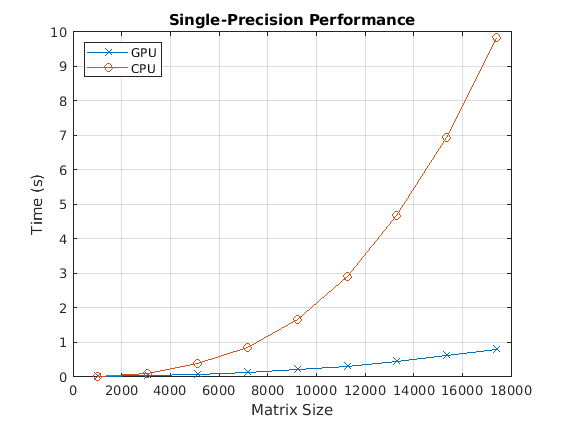
まず、単精度のバックスラッシュ演算子のパフォーマンスを確認します。

fig = figure;
ax = axes('parent', fig);
plot(ax, results.sizeSingle, results.timeSingleGPU, '-x', ...
     results.sizeSingle, results.timeSingleCPU, '-o')
grid on;
legend('GPU', 'CPU', 'Location', 'NorthWest');
title(ax, 'Single-Precision Performance')
ylabel(ax, 'Time (s)');
xlabel(ax, 'Matrix Size');

Figure contains an axes object. The axes object with title Single-Precision Performance, xlabel Matrix Size, ylabel Time (s) contains 2 objects of type line. These objects represent GPU, CPU.

drawnow;

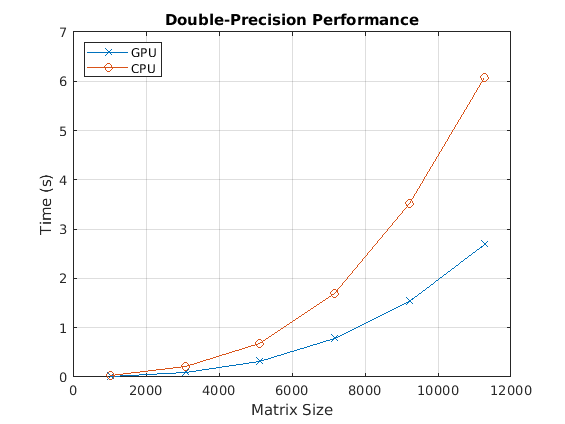
次に、倍精度のバックスラッシュ演算子のパフォーマンスを確認します。

fig = figure;
ax = axes('parent', fig);
plot(ax, results.sizeDouble, results.timeDoubleGPU, '-x', ...
     results.sizeDouble, results.timeDoubleCPU, '-o')
legend('GPU', 'CPU', 'Location', 'NorthWest');
grid on;
title(ax, 'Double-Precision Performance')
ylabel(ax, 'Time (s)');
xlabel(ax, 'Matrix Size');

Figure contains an axes object. The axes object with title Double-Precision Performance, xlabel Matrix Size, ylabel Time (s) contains 2 objects of type line. These objects represent GPU, CPU.

drawnow;

最後に、GPU と CPU を比較したときのバックスラッシュ演算子の高速化を確認します。

speedupDouble = results.timeDoubleCPU./results.timeDoubleGPU;
speedupSingle = results.timeSingleCPU./results.timeSingleGPU;
fig = figure;
ax = axes('parent', fig);
plot(ax, results.sizeSingle, speedupSingle, '-v', ...
     results.sizeDouble, speedupDouble, '-*')
grid on;
legend('Single-precision', 'Double-precision', 'Location', 'SouthEast');
title(ax, 'Speedup of Computations on GPU Compared to CPU');
ylabel(ax, 'Speedup');
xlabel(ax, 'Matrix Size');

Figure contains an axes object. The axes object with title Speedup of Computations on GPU Compared to CPU, xlabel Matrix Size, ylabel Speedup contains 2 objects of type line. These objects represent Single-precision, Double-precision.

drawnow;

参考

関数

codegen | coder.gpu.kernel | coder.gpu.kernelfun | gpucoder.matrixMatrixKernel | coder.gpu.constantMemory | stencilfun | coder.checkGpuInstall

オブジェクト

coder.gpuConfig | coder.CodeConfig | coder.EmbeddedCodeConfig | coder.gpuEnvConfig