このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

surrogateoptを使って実現可能性問題を解く、問題ベース

ライブ スクリプトを開く

一部の問題では、最小化すべき目的関数を持たずに、すべての制約を満たす点を見つける必要があります。たとえば、次のような制約があるとします。

(y+x2)2+0.1y2≤1y≤exp(-x)-3y≤x-4.

いずれかの点 (x,y) が制約を満たしていますか?この質問に答えるには、さまざまなポイントで式を評価する必要があります。surrogateopt ソルバーでは、初期点を指定する必要がなく、広範囲のポイント セットを探索します。したがって、surrogateopt は実現可能性の問題に適しています。

制約を視覚化するには、「制約の視覚化」を参照してください。この問題に対するソルバーベースのアプローチについては、実現可能性問題を解決する を参照してください。

メモ: この例では、2 つのヘルパー関数 outfun と evaluateExpr を使用します。各関数のコードは この例の最後 に記載されています。各関数のコードがスクリプトの最後またはパス上のファイルに含まれていることを確認してください。

実現可能性問題の設定

問題ベースのアプローチの場合、最適化変数 x と y を作成し、リストされた制約の式を作成します。surrogateopt ソルバーを使用するには、すべての変数に対して有限の境界を設定する必要があります。下限を -10、上限を 10 に設定します。

x = optimvar("x","LowerBound",-10,"UpperBound",10);
y = optimvar("y","LowerBound",-10,"UpperBound",10);
cons1 = (y + x^2)^2 + 0.1*y^2 <= 1;
cons2 = y <= exp(-x) - 3;
cons3 = y <= x - 4;

最適化問題を作成し、問題に制約を含めます。

prob = optimproblem("Constraints",[cons1 cons2 cons3]);

この問題には目的関数がありません。内部的には、ソルバーはすべてのポイントに対して目的関数の値を 0 に設定します。

問題を解く

surrogateopt を使用して、問題を解きます。

rng(1) % For reproducibility
[sol,fval] = solve(prob,"Solver","surrogateopt")
Solving problem using surrogateopt.

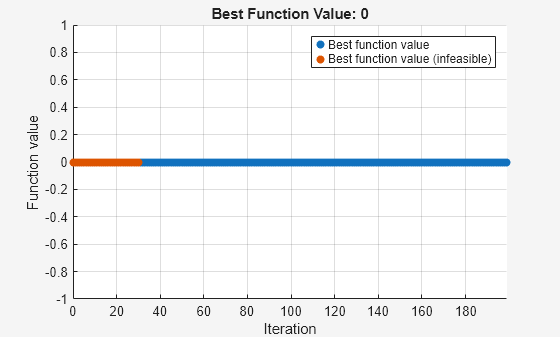
Figure Optimization Plot Function contains an axes object. The axes object with title Best Function Value: 0, xlabel Iteration, ylabel Function value contains 2 objects of type scatter. These objects represent Best function value, Best function value (infeasible).

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = struct with fields:
    x: 1.7435
    y: -3.1255


fval = 
0

プロット内の赤色で示されているように、評価された最初のいくつかのポイントは実行不可能です。約 60 回の評価の後、ソルバーは実行可能なポイントを見つけ、青でプロットします。

返されたソリューションで実現可能性を確認します。

infeasibility(cons1,sol)
ans = 
0

infeasibility(cons2,sol)
ans = 
0

infeasibility(cons3,sol)
ans = 
0

すべての実行不可能性がゼロであるため、点 sol は実行可能であることがわかります。

最初の実行可能なポイントでソルバーを停止する

より速く解に到達するには、実行可能なポイントに到達するたびにソルバーを停止する出力関数 (出力関数 を参照) を作成します。この例の最後にある outfun ヘルパー関数は、制約違反のないポイントに到達するとソルバーを停止します。

outfun 出力関数を使用して問題を解決します。

opts = optimoptions("surrogateopt","OutputFcn",@outfun);
rng(1) % For reproducibility
[sol,fval] = solve(prob,"Solver","surrogateopt","Options",opts)
Solving problem using surrogateopt.

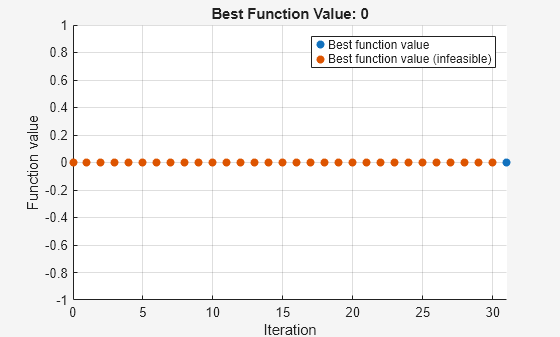
Figure Optimization Plot Function contains an axes object. The axes object with title Best Function Value: 0, xlabel Iteration, ylabel Function value contains 2 objects of type scatter. These objects represent Best function value, Best function value (infeasible).

Optimization stopped by a plot function or output function.

sol = struct with fields:
    x: 1.7435
    y: -3.1255


fval = 
0

今回は、ソルバーは以前よりも早く停止します。

制約の可視化

制約を可視化するには、fimplicit を使用して、各制約関数がゼロになる点をプロットします。関数 fimplicit は数値をその関数に渡す一方、関数 evaluate は構造体を必要とします。これらの関数を結合するには、補助関数 evaluateExpr (この例の終わりに掲載) を使用します。この関数は、単に渡された値を適切な名前の構造体に格納します。

関数 evaluateExpr がベクトル化された入力に対応していないために発生する警告を回避します。返された解の点を緑色の円としてプロットします。

s = warning('off','MATLAB:fplot:NotVectorized');
figure
cc1 = (y + x^2)^2 + 0.1*y^2 - 1;
fimplicit(@(a,b)evaluateExpr(cc1,a,b),[-2 2 -4 2],'r')
hold on
cc2 = y - exp(-x) + 3;
fimplicit(@(a,b)evaluateExpr(cc2,a,b),[-2 2 -4 2],'k')
cc3 = y - x + 4;
fimplicit(@(x,y)evaluateExpr(cc3,x,y),[-2 2 -4 2],'b')
plot(sol.x,sol.y,'og')
hold off

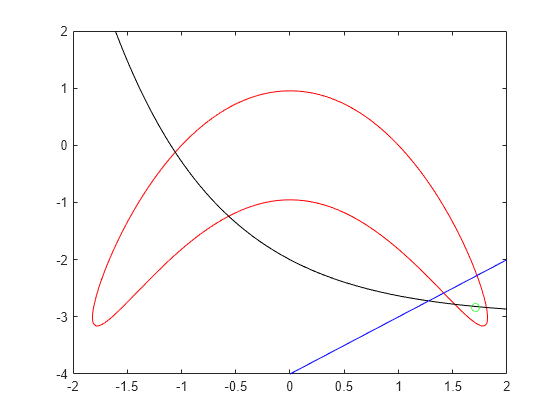
Figure contains an axes object. The axes object contains 4 objects of type implicitfunctionline, line. One or more of the lines displays its values using only markers

warning(s);

実行可能領域は、赤線で囲まれた範囲の内側にあり、かつ黒線および青線の下側になります。つまり、実行可能領域は、赤線で囲まれた範囲の右下です。

補助関数

次のコードは、補助関数 outfun を作成します。

function stop = outfun(~,optimValues,state)
stop = false;
switch state
    case 'iter'
        if optimValues.currentConstrviolation <= 0
            stop = true;
        end
end
end

次のコードは、補助関数 evaluateExpr を作成します。

function p = evaluateExpr(expr,x,y)
pt.x = x;
pt.y = y;
p = evaluate(expr,pt);
end

参考

| |

トピック