このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

patternsearchを使った非滑らかな関数の最適化、問題ベース

この例では、問題ベースのアプローチで直接探索を使用して、滑らかでない関数を最小化する方法を示します。この例を実行すると、最小化する関数 ps_example(x) が含まれます。

目的関数をプロットします。

fsurf(@(x,y)reshape(ps_example([x(:),y(:)]),size(x)),...
    [-6 2 -4 4],"LineStyle","none","MeshDensity",300)
colormap 'jet'
view(-26,43)
xlabel("x(1)")
ylabel("x(2)")
title("ps\_example(x)")

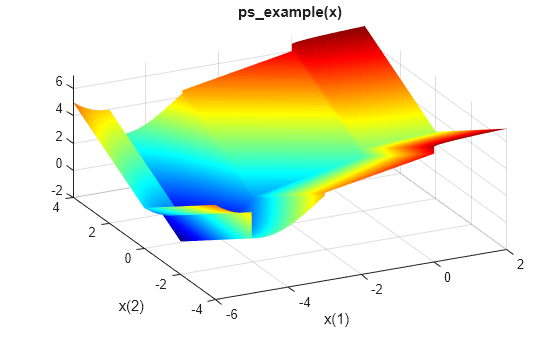
2 次元最適化変数 x を作成します。ps_example 関数は変数が行ベクトルであると想定しているため、x を 2 要素の行ベクトルとして指定します。

x = optimvar("x",1,2);

ps_example を目的関数として使用するには、fcn2optimexpr を使用して関数を最適化式に変換します。

fun = fcn2optimexpr(@ps_example,x);

目的関数 ps_example を使用して最適化問題を作成します。

prob = optimproblem("Objective",fun);

初期点 x0 を、フィールド x が値 [2.1 1.7] を取る構造体として指定します。

x0.x = [2.1 1.7];

patternsearch ソルバーを指定して問題を解きます。

[sol,fval] = solve(prob,x0,"Solver","patternsearch")

Solving problem using patternsearch.
patternsearch stopped because the mesh size was less than options.MeshTolerance.

sol = struct with fields:
    x: [-4.7124 -7.6294e-07]

fval = 
-2.0000

patternsearch はデフォルトの fminunc ソルバーよりも優れたソリューション (より低い関数値) を見つけますが、滑らかでない関数を最小化する場合には推奨されません。

[solfminunc,fvalfminunc] = solve(prob,x0)

Solving problem using fminunc.

Local minimum possible.

fminunc stopped because it cannot decrease the objective function
along the current search direction.

<stopping criteria details>

solfminunc = struct with fields:
    x: [1.9240 8.8818e-16]

fvalfminunc = 
2.9161

参考

patternsearch | fcn2optimexpr | solve

トピック

• 直接探索