非正規数の実行速度

非正規数は、浮動小数点の文献で以前は非正規化数と呼ばれており、浮動小数点演算においてゼロ周辺のアンダーフローのギャップを埋めます。非正規値とは、0.0 に近すぎるため正規化値として表記できない、特殊なカテゴリの浮動小数点値です。非正規数の仮数の先頭はゼロです。浮動小数点の加算と減算を行うときに、非正規数によってアンダーフローが回避されます。

非正規数の使用によって正規表現を上回る精度が提供されます。仮数の先頭にゼロを使用することで、正規表現がその最小指数に達した後のさらに小さい値を表現します。値が 0.0 に近づくと、拡張範囲と精度がトレードオフされます。アプリケーションで追加の範囲が必要である場合、非正規数は便利です。

ただし、リアルタイムシステムで非正規数を使用すると、実行のレイテンシが著しく増加し、設計マージンが過剰になり、リアルタイムのオーバーランが発生します。シミュレーションまたは生成コードが非正規数を生成または使用する計算を実行すると、正規数による類似計算よりも実行速度が 50 倍遅くなる可能性があります。非正規数計算の実際のシミュレーションまたはコード実行時間は、コンピューターの動作環境によって異なります。通常、デスクトッププロセッサの場合、非正規数計算の実行時間は、正規数の同様の計算より 5 倍かかります。

非正規数計算のレイテンシのために実行に時間がかかったり、オーバーランする可能性を低減するために、以下のいずれかを行います。

モデルでのウォッシュアウト、フィルターなどの入力や主な演算では、入力または計算された非正規値はすべて手動で削除してゼロにします。例については、非正規数をゼロにフラッシュするを参照してください。
単精度の 32 ビット浮動小数点数の非正規値を検出するには、次の手順に従います。
1. MATLAB^® ホストで最小正規数を検出します。コマンドウィンドウで以下のように入力します。
```
>> SmallestNormalSingle = realmin('single')
```
  C 言語では、float.h で定義された FLT_MIN は realmin('single') と等価です。
2. 以下の範囲内で値を検索します。
```
 0 < fabsf(x) < SmallestNormalSingle 
```
倍精度の 64 ビット浮動小数点数の非正規値を検出するには、次の手順に従います。
1. MATLAB ホストで最小正規数を検出します。コマンドウィンドウで以下のように入力します。
```
>> SmallestNormalDouble = realmin('double') 
```
  C 言語では、float.h で定義された DBL_MIN は realmin('double') と等価です。
2. 非正規値を検出するため、以下の範囲内で値を検索します。
```
0 < fabs(x) < SmallestNormalDouble
```
[非正規数に対するシミュレーションの動作] パラメーターを Flush to zero (FTZ) に設定して、算術演算からのすべての非正規結果についての flush-to-zero 動作をエミュレートします。詳細については、非正規数に対するシミュレーションの動作を参照してください。
プロセッサでは、flush-to-zero モードを設定するか、コンパイラで非正規数を無効にするオプションを指定します。flush-to-zero モードでは、非正規数が浮動小数点演算に対する入力である場合、非正規数は 0 として扱われます。アンダーフローの例外は、flush-to-zero モードでは起こりません。
たとえば、Intel^® プロセッサでは、MXCSR レジスタの flush-to-zero (FTZ) および denormals-are-zero (DAZ) フラグが浮動小数点計算を制御します。Linux の gcc コンパイラの場合、 -ffast-math は突発的アンダーフロー (FTZ) である flush-to-zero を設定しますが、–O3 -ffast-math は非正規数を使用して段階的アンダーフローに戻します。

詳細は、IEEE^® 標準 754 の IEEE Standard for Floating-Point Arithmetic を参照してください。

非正規数を使用する場合と使用しない場合のシミュレーション時間

この例では、非正規数の使用によりシミュレーション時間が約 5 倍に増加することを示します。

この例のために、Constant ブロックと Gain ブロックをもつシンプルなモデル ex_subnormal を作成します。[ゲイン] は非正規値 realmin('double')/2 に設定されています。

シミュレーションを実行するには、コマンドウィンドウで「for k=1:5, tic; sim('ex_subnormal'); toc,end」と入力します。非正規値を使用するシミュレーションの経過時間を確認すると、以下のようになります。

>> for k=1:5, tic; sim('ex_subnormal'); toc,end
Elapsed time is 9.909326 seconds.
Elapsed time is 9.617966 seconds.
Elapsed time is 9.797183 seconds.
Elapsed time is 9.702397 seconds.
Elapsed time is 9.893946 seconds.

[Gain] を非正規値ではない数 2 に設定します。

>> set_param('ex_subnormal/Gain', 'Gain', '2');

シミュレーションを実行するには、コマンドウィンドウで「for k=1:5, tic; sim('ex_subnormal'); toc,end」と入力します。非正規値を使用しないシミュレーションの経過時間を確認すると、以下のようになります。

>> for k=1:5, tic; sim('ex_subnormal'); toc,end
Elapsed time is 2.045123 seconds.
Elapsed time is 1.796598 seconds.
Elapsed time is 1.758458 seconds.
Elapsed time is 1.721721 seconds.
Elapsed time is 1.780569 seconds.

非正規数をゼロにフラッシュする

この例では、単精度非正規数をゼロにフラッシュする方法を示します。

この例のために、シンプルなモデル ex_flush_to_zero を作成します。
- Repeating Sequence Stair は 2 の 0 乗から 2 の -165 乗の値までの数列を生成します。数列はゼロに近くなります。
- ConditionRealScalar は、realmin('single') より小さい非正規の単精度値をゼロにフラッシュします。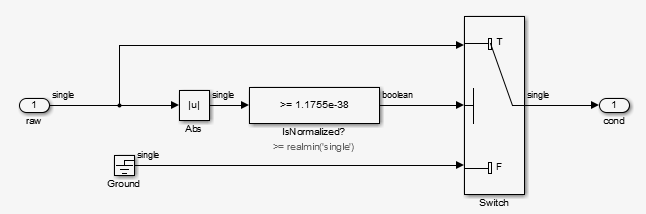
- MATLAB 関数ブロック log2 は Repeating Sequence Stair 出力の 2 を底とする対数を生成します。具体的には、log2 は 0 から -165 の数値を生成します。
  function y = fcn(u) %#codegen y = log2(u); end
[シミュレーション] 、 [ステップを戻す] 、 [シミュレーションステップの設定] ペインで次を実行します。
- [ステップを戻す機能を有効にする] を選択します。
- [次の時間に達したときにシミュレーションを一時停止] を選択して 121 と入力します。
モデルウィンドウで、シミュレーションを実行します。シミュレーションは T=121 で停止します。表示される値は次のとおりです。
- ConditionRealScalar 出力がゼロに近づきます。
- Repeating Sequence Stair output がゼロに近づきます。
シミュレーションを T=127 まで進めます。ConditionRealScalar は非正規値出力を Repeating Sequence Stair からゼロにフラッシュします。
引き続きシミュレーションを進めます。ConditionRealScalar は非正規単精度値出力を Repeating Sequence Stair からゼロにフラッシュします。T=150 の場合、Repeating Squence Stair の出力自体はゼロです。