モデルと生成されたコードのシミュレーション結果における数値の整合性

モデルベースデザインのワークフローで、MathWorks^® 製品を使用して固定小数点および浮動小数点演算を使用する数値アプリケーション用のコードを生成します。

モデルを生成するには、MATLAB^®、Simulink^® および Stateflow^® を使用します。
ソースコードを生成するには、Simulink Coder™ と Embedded Coder^® を使用します。
モデルと生成されたコード間の数値的等価性をテストするには、モデルと生成されたコードのシミュレーション結果を比較します。たとえば、ノーマルモードのシミュレーション結果をソフトウェアインザループ (SIL) シミュレーション結果と比較します。

モデルと生成されたコードのシミュレーションの結果は、以下の場合、数値的に整合しています。

シミュレーションデータインスペクターを使用して結果を比較します。不一致が存在するかどうかや、不一致が大きいかどうかを判別するために、絶対許容誤差の値と相対許容誤差の値を指定できます。

固定小数点アプリケーションの場合、ゼロの絶対許容誤差を指定できます。
浮動小数点アプリケーションの場合、参照値または信号に関する許容誤差を指定できます。参照の選択はアプリケーションに依存します。以下の例について考えます。
- 反復するフィードフォワードエラー計算で線形の代数方程式を解くアルゴリズム。eps に対する許容誤差を指定できます。
- 閉ループシステムの比例-積分-微分 (PID) コントローラー。過渡動作の場合、標準から条件を使用して許容誤差を指定できます。定常状態動作の場合、PID コントローラーの特性を基準にして許容誤差を指定できます。

Simulink.sdi.Signal オブジェクトの absTol および relTol プロパティを使用して、プログラムにより絶対許容誤差の値と相対許容誤差の値を指定できます。

複雑なシステムの場合、モデルと生成されたコードのシミュレーションにおける数値の差は、システムを介して伝播するブロックレベルの差が原因として考えられます。システムレベルで数値の差を観察する場合、次を行います。

以下のプラントコントローラーモデルを検討します。

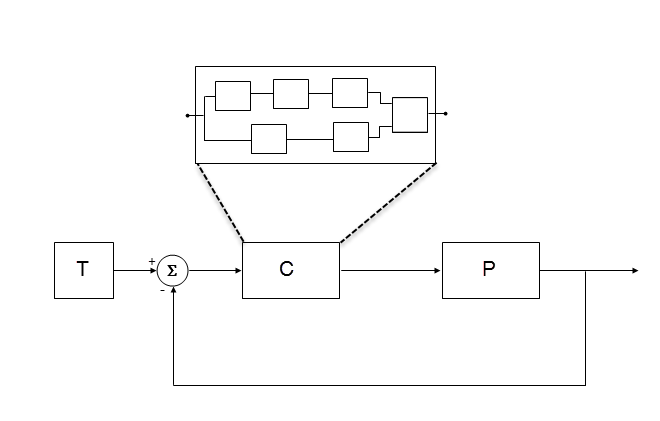
T は、基準信号またはテスト信号を生成します。
C はコントローラーコンポーネントです。コントローラー出力はプラント入力です。C は複数の Model ブロックを構成する Model ブロックである可能性があります。
P はプラントコンポーネントです。プラント出力は基準信号から減算され、コントローラー入力を生成します。

モデルコントローラーと生成されたコードバージョンの間の数値的等価性をテストするには、次を行います。

シミュレーションデータインスペクターの比較により一致が示される場合、モデルと生成されたコードの結果は数値的に整合しています。

ノーマルモードの出力と SIL モードの出力が一致しない場合、次を行います。

メモ

大量の信号を比較しなければならない場合は、Simulink Test™ でワークフローを自動化できます。SIL Verification for a Subsystem (Simulink Test)を参照してください。

固定小数点および浮動小数点アプリケーション開発では、モデルと生成されたコードのシミュレーションから得られるブロックレベルの結果間の数値的な一致に影響する可能性のある要因があります。

一部の要因は固定小数点および浮動小数点アプリケーションの両方に影響します。たとえば、以下の使用などです。

浮動小数点アプリケーションのみに影響する要因もあります。以下に例を示します。

参照

[1] IEEE^® Standard on Transitions, Pulses, and Related Waveforms, IEEE Standard 181, 2003, pp. 15–17.