移動平均フィルターと FIR フィルターの違いとは

移動平均フィルターは、標準 FIR フィルターの特殊なケースです。両方のフィルターに有限インパルス応答があります。移動平均フィルターはスケーリングされた 1 のシーケンスを係数として使用しますが、FIR フィルターの係数はフィルター仕様に基づいて設計されます。これらは通常、1 のシーケンスではありません。

ストリーミングデータの移動平均は、有限スライディングウィンドウを使用して計算されます。

$m o v A v g = \frac{x [n] + x [n - 1] + ... + x [n - N]}{N + 1}$

N + 1 はフィルターの長さです。このアルゴリズムは、係数ベクトルが [b₀, b₁, ..., b_N] である標準 FIR フィルターの特殊なケースです。

$F I R O u t p u t = b_{0} x [n] + b_{1} x [n - 1] + ... + b_{N} x [n - N]$

出力を計算するには、標準 FIR フィルターは各データサンプルに [b₀, b₁, ..., b_N] ベクトルの係数を乗算し、結果を加算します。移動平均フィルターは乗算器を使用しません。アルゴリズムは、すべてのデータサンプルを加算し、結果と 1 / filterLength を乗算します。

移動平均フィルターと FIR フィルターの周波数応答

ライブスクリプトを開く

移動平均フィルターの周波数応答と標準 FIR フィルターの周波数応答を比較します。標準 FIR フィルターの係数をスケーリングされた 1 のシーケンスとして設定します。スケーリング係数は 1/|filterLength| です。

dsp.FIRFilter System object™ を作成して、その係数を 1/40 に設定します。移動平均を計算するには、スライディングウィンドウの長さが 40 の dsp.MovingAverage System object を作成します。両方のフィルターの係数は同じです。入力は平均 0、標準偏差 1 のガウスホワイトノイズです。

filter = dsp.FIRFilter('Numerator',ones(1,40)/40);
mvgAvg = dsp.MovingAverage(40);
input = randn(1024,1);
filterOutput = filter(input);
mvgAvgOutput = mvgAvg(input);

fvtool を使用して両方のフィルターの周波数応答を可視化します。

hfvt = fvtool(filterOutput,1,mvgAvgOutput,1);
legend(hfvt,'FIR Filter','Moving Average Filter');

周波数応答が厳密に一致し、これは移動平均フィルターが FIR フィルターの特殊なケースであることを証明しています。

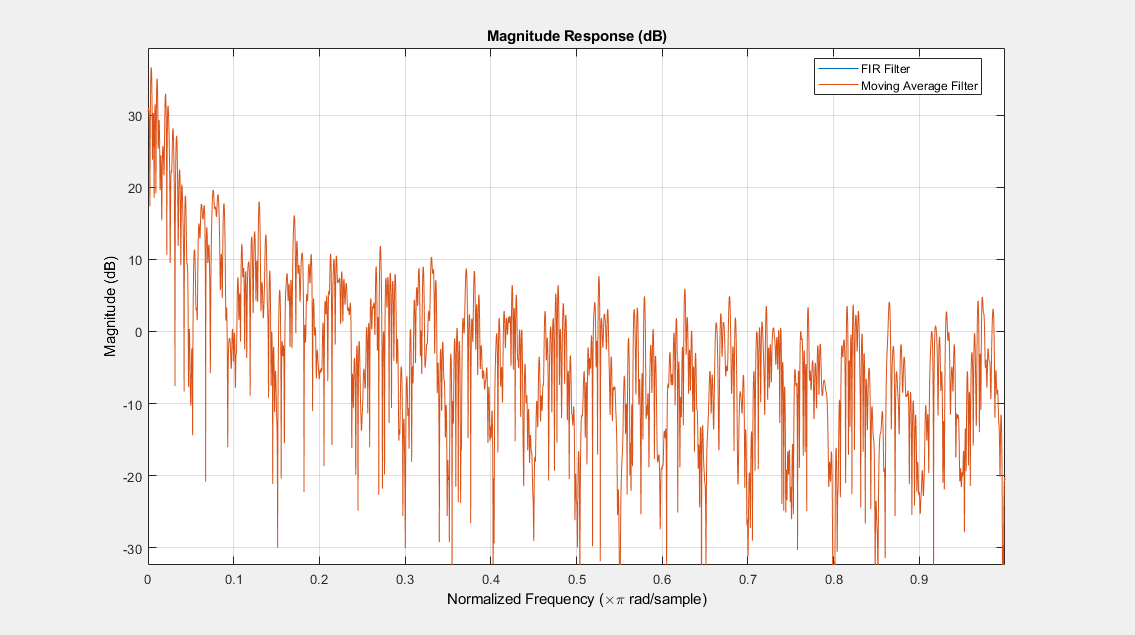
比較のために、フィルターの周波数応答をノイズなしで表示します。

fvtool(filter);

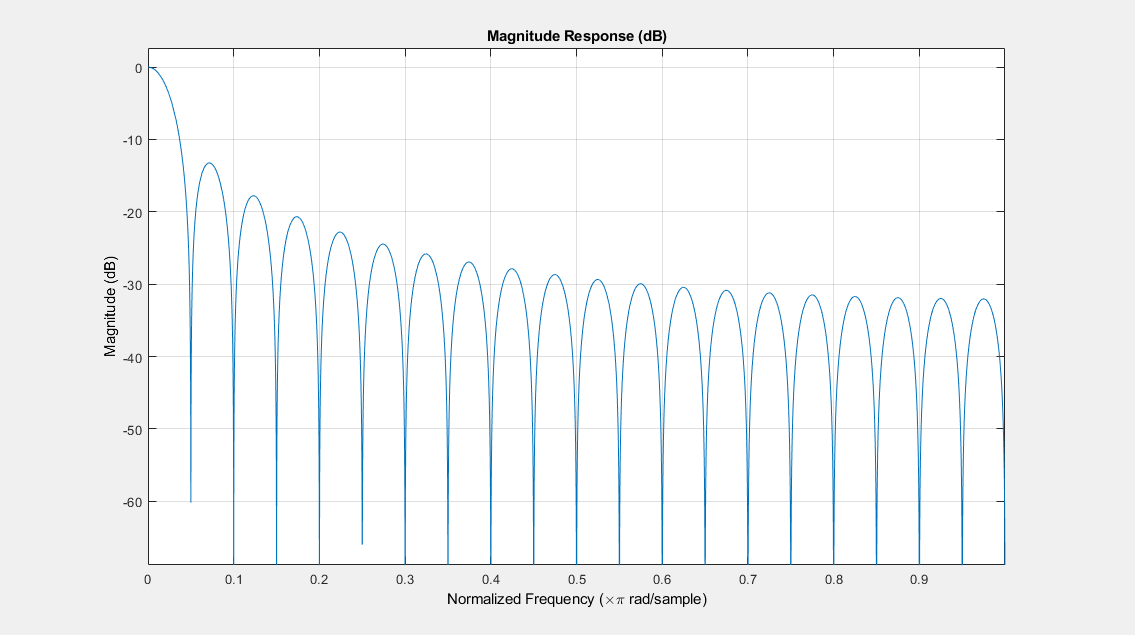
フィルターの周波数応答を理想フィルターの周波数応答と比較します。通過帯域のメインローブがフラットではなく、阻止帯域のリップルは制限されていないことがわかります。移動平均フィルターの周波数応答は、理想フィルターの周波数応答とは一致しません。

理想 FIR フィルターを実現するには、フィルター係数をスケーリングされた 1 のシーケンスではないベクトルに変更します。フィルターの周波数応答が変更され、理想フィルターの応答に近づく傾向があります。

事前定義されたフィルター仕様に基づきフィルター係数を設計します。たとえば、正規化されたカットオフ周波数が 0.1、通過帯域リップルが 0.5、阻止帯域の減衰量が 40 dB の等リップル FIR フィルターを設計します。fdesign.lowpass を使用してフィルター仕様を定義し、design メソッドを使用してフィルターを設計します。

FIReq = fdesign.lowpass('N,Fc,Ap,Ast',40,0.1,0.5,40);
filterCoeff = design(FIReq,'equiripple','SystemObject',true);
fvtool(filterCoeff)

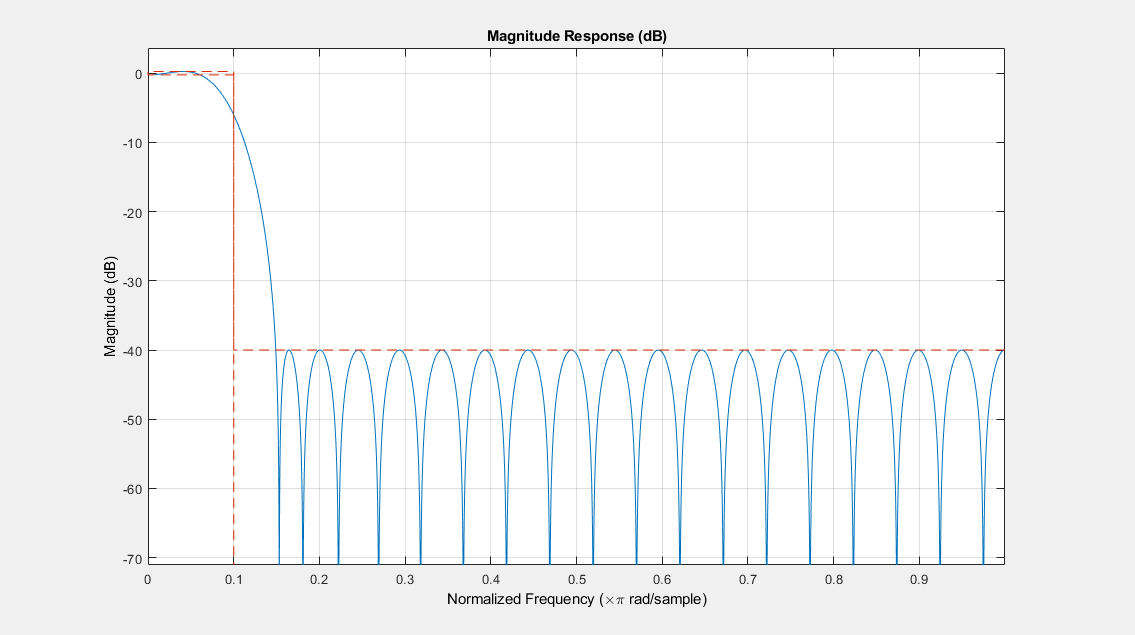
通過帯域のフィルターの応答はほぼフラット (理想的な応答と同様) であり、阻止帯域には制約付き等リップルがあります。

移動平均フィルターと FIR フィルターの違いとは

移動平均フィルターと FIR フィルターの周波数応答

関連するトピック