ストリーミング信号の統計

ライブスクリプトを開く

この例では、MATLAB® コマンドラインで使用可能な DSP System Toolbox™ の機能を使用して、入力データストリームの統計測定を実行する方法を示します。信号の統計、最小値、最大値、平均値、分散、ピークと平方根平均二乗および信号のパワースペクトル密度を計算してプロットします。

はじめに

この例では DSP System Toolbox System object を使用して信号統計を計算します。これらのオブジェクトは状態を自動的に処理するため、状態の更新に必要なコードの量が減り、コード作成時のエラーの低減につながります。

これらの System object は、処理で使用される多くの値を事前に計算します。これはループ内の同じプロパティの信号を処理する場合に大変便利です。たとえば、スペクトル推定アプリケーションで FFT を計算する場合、入力のプロパティがわかっていれば正弦値および余弦値を計算して保存しておき、以降の呼び出しでこれらの値を再利用することができます。また、オブジェクトは入力プロパティが各呼び出しの以前の入力と同じタイプのプロパティかどうかのみを確認します。

初期化

ここではコードに使用されている一部の変数を初期化し、処理に使用される System object をインスタンス化します。これらのオブジェクトは必要な変数またはテーブルも事前に計算するため、ループ内で以降の呼び出しを効率よく処理できます。

frameSize = 1024; % Size of one chunk of signal to be processed in one loop
Fs = 48e3;        % Sample rate
numFrames = 100;  % number of frames to process

この例の入力信号は、ローパス FIR フィルターを通して渡されるホワイトガウスノイズです。ノイズ信号をフィルター処理するために使用される FIR フィルター System object™ を作成します。

fir = dsp.FIRFilter('Numerator',fir1(32,.3));

スペクトル推定器 System object を作成して、入力のパワースペクトル密度を推定します。

spect = dsp.SpectrumEstimator('SampleRate',Fs,...
                              'SpectrumType','Power density',...
                              'FrequencyRange','onesided',...
                              'Window','Kaiser');

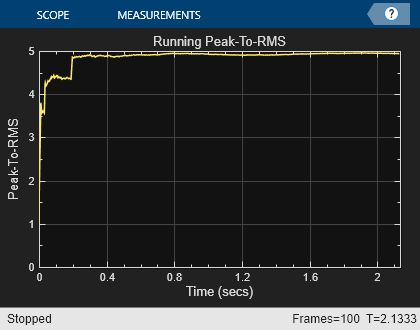
平均値、分散、ピークと平方根平均二乗間、最大値および最小値を計算する System object を作成し、これをランニングモードに設定します。これらのオブジェクトは、統計 System object のサブセットとして本製品で利用できます。ランニングモードでは、現在の入力の統計だけでなく、過去の全体にわたる入力の統計を計算します。

runMean       = dsp.MovingAverage('SpecifyWindowLength', false);
runVar        = dsp.MovingVariance('SpecifyWindowLength', false);
runPeaktoRMS  = dsp.PeakToRMS('RunningPeakToRMS',true);
runMin        = dsp.MovingMinimum('SpecifyWindowLength', false);
runMax        = dsp.MovingMaximum('SpecifyWindowLength', false);

統計とスペクトルの可視化に使用されるスコープ System object を初期化します。

meanScope = timescope('SampleRate',Fs,...
                      'TimeSpanSource','property',...
                      'TimeSpan',numFrames*frameSize/Fs,...
                      'Title','Running Mean',...
                      'YLabel','Mean',...
                      'YLimits',[-0.1 .1],...
                      'Position',[43   308   420   330]);
p2rmsScope = timescope('SampleRate',Fs,...
                       'TimeSpanSource','property',...                           
                       'TimeSpan',numFrames*frameSize/Fs,...
                       'Title','Running Peak-To-RMS',...
                       'YLabel','Peak-To-RMS',...
                       'YLimits',[0 5],...
                       'Position',[480   308   420   330]);
minmaxScope = timescope('SampleRate',Fs,...
                        'TimeSpanSource','property', ...                         
                        'TimeSpan',numFrames*frameSize/Fs,...
                        'ShowGrid',true,...
                        'Title',...
                            'Signal with Running Minimum and Maximum',...
                        'YLabel','Signal Amplitude',...
                        'YLimits',[-3 3],...
                        'Position',[43   730   422   330]);
spectrumScope = dsp.ArrayPlot('SampleIncrement',...
                             .5 * Fs/(frameSize/2 + 1 ),...
                             'PlotType','Line',...
                             'Title','Power Spectrum Density',...
                             'XLabel','Frequency (Hz)',...
                             'YLabel','Power/Frequency (dB/Hz)',...
                             'YLimits',[-120 -30],...
                             'Position',[475 730 420 330]);

ストリーム処理ループ

ここで、System object を使用して、ホワイトガウスノイズをフィルター処理してその平均値、分散、ピークと平方根平均二乗間、最小値、最大値およびスペクトルを計算する処理ループを呼び出します。

System object がループの内部で呼び出されることに注意してください。入力データプロパティは変わらないため、オブジェクトを再利用でき、メモリ使用量が少なくなります。

for i=1:numFrames
    % Pass white Gaussian noise through FIR Filter
    sig = fir(randn(frameSize,1));

    % Compute power spectrum density
    ps = spect(sig);
   
    % The runMean System object keeps track of the information about past
    % samples and gives you the mean value reached until now. The same is
    % true for runMin and runMax System objects.
    meanval  = runMean(sig);
    variance = runVar( sig);
    peak2rms = runPeaktoRMS(sig);
    minimum  = runMin( sig);
    maximum  = runMax(sig);

    % Plot the data you have processed
    minmaxScope([sig,minimum,maximum]);
    spectrumScope(10*log10(ps));
    meanScope(meanval);
    p2rmsScope(peak2rms);
end
release(minmaxScope);

release(spectrumScope);

release(meanScope);

release(p2rmsScope);

まとめ

コードでは、適切な入力引数を使用して連続する System object の呼び出しだけが行われ、統計を計算するのにインデックスやカウンターなどの変数の維持を必要としないことを視覚的に確認しました。この手法により、コード作成が短時間で済み、エラーもなくなります。オブジェクト内の定数変数を事前に計算することで、一般に処理時間が短縮されます。