任意の振幅と位相フィルター設計
この例では、カスタマイズされた振幅と位相の仕様をもつフィルターを設計する方法を示します。多くのフィルター設計問題では、対称性によって線形の位相応答が得られるという前提で、振幅応答のみに焦点が当てられています。しかし、場合によっては、目的とするフィルターが振幅の制約も位相の制約も満たす必要があります。
たとえば、カスタムの振幅と位相設計仕様は、データ伝送システムにおける振幅と位相の歪みのイコライズ (チャネルのイコライズ) またはオーバーサンプリングされた ADC における振幅と位相の歪みのイコライズ (望ましくないハードウェア特性の補正など) に使用できます。別の用途としては、線形位相フィルターよりも小さい群遅延と特定の次数の最小位相フィルターよりも低い歪みをもつフィルターの設計があります。
周波数応答仕様とフィルター設計
フィルター応答は通常、周波数範囲 (帯域) および各帯域で目的とするゲインによって指定されます。カスタムの振幅と位相フィルター仕様も同様ですが、位相応答も含まれており、通常は複素数値としてゲインと位相応答はともに符号化されます。ほとんどの場合、応答仕様は周波数ベクトル F = [f1, ..., fN] ("N" は増加する周波数) と、フィルターの複素応答値に対応する周波数応答ベクトル H = [h1, ..., hN] から構成されます。DSP System Toolbox™ では、designfiltの arbmagnphasefir および arbmagnphaseiir の応答を使用して、目的の周波数応答をもつフィルター オブジェクトを設計することができます。FIR 設計アルゴリズムおよび IIR 設計アルゴリズムの詳細については、[1]を参照してください。
FIR 設計
この最初の例では、いくつかの FIR 設計法を比較して、複素 RF バンドパス フィルターの振幅と位相をモデル化します。まず、周波数をベクトル "F"、複素応答値をベクトル "H" として目的のフィルター仕様を読み込みます。左と右のグラフにゲインと位相周波数応答をそれぞれプロットします。
load('gainAndPhase','F','H') % Load frequency response data plotResponse(F, H) % A helper plotting function used in this demo

引数 FilterOrder、Frequencies、および FrequencyResponse を指定し、designfilt の arbmagnphasefir 応答を使用して任意応答 FIR フィルターを設計します。これにより、ナイキスト範囲全体にわたって目的の応答 (つまり、緩和された "don't care" 領域のないシングルバンド仕様) を指定できます。この例で、目的の応答データ ベクトル "F" と "H" の点数は 655 点であり、周波数領域全体で比較的密になっています。
各入力引数セットでサポートされる設計手法の一覧については、designfiltの "argmagnphasefir" フィルター応答を参照してください。引数 FilterOrder、Frequencies、および FrequencyResponse を指定した場合、サポートされる設計手法は、equiripple、ls、および freqsamp です。利用可能な手法を使用して、任意応答 FIR フィルターを設計します。
N = 100; Hd1=designfilt('arbmagnphasefir',Frequencies=F,FrequencyResponse=H,... FilterOrder=N,DesignMethod='equiripple',SystemObject=true); Hd2=designfilt('arbmagnphasefir',Frequencies=F,FrequencyResponse=H,... FilterOrder=N,DesignMethod='ls',SystemObject=true); Hd3=designfilt('arbmagnphasefir',Frequencies=F,FrequencyResponse=H,... FilterOrder=N,DesignMethod='freqsamp',SystemObject=true);
フィルターの周波数応答および公称応答を破線でプロットします。等リップル設計 Hd1 は通過帯域で非常に良好な近似であるように見えますが、他の領域ではやや逸脱しています。最小二乗設計 Hd2 は均一重み付け 2 次ノルムに最適化されており (どの領域にも有利ではない)、周波数サンプリングされた FIR 設計 Hd3 は 3 通りすべての中で近似が最も良くないように見えます。
figure [H1,W] = freqz(Hd1); H2 = freqz(Hd2); H3 = freqz(Hd3); plot(W/pi,db(H1)) hold on plot(W/pi,db(H2)) plot(W/pi,db(H3)) plot(F,db(H),'k--') hold off legend('Equiripple Hd(1)', 'FIR Least-Squares Hd(2)','Frequency Sampling Hd(3)','Nominal Response',Location = 'NorthEast')

[P1,W] = phasez(Hd1); P2 = phasez(Hd2); P3 = phasez(Hd3); plot(W/pi,P1) hold on plot(W/pi,P2) plot(W/pi,P3) plot(F,unwrap(angle(H))+2*pi,'k--') hold off legend('Equiripple Hd1', 'FIR Least-Squares Hd2','Frequency Sampling Hd3','Nominal Response')

IIR 設計
次に、IIR フィルターを設計します。目的のフィルターは、通過帯域に線形位相をもつハーフバンド ハイパス フィルターです。次の図に示すように、この仕様は周波数領域の 100 個の点で与えられます。
F = [linspace(0,.475,50) linspace(.525,1,50)]; H = [zeros(1,50) exp(-1j*pi*13*F(51:100))]; plotResponse(F, H)

シングルバンド設計仕様を指定し、designfilt の argbmagnphaseiir 応答を使用して任意応答 IIR を作成します。これは、引数 NumeratorOrder、DenominatorOrder、Frequencies、および FrequencyResponse を指定することで実行できます。この仕様の場合、利用可能な設計法は 1 つしかありません (最小二乗 IIR 設計 ls)。
ls 設計法では異なる周波数に対して別の重みを指定できるため、各帯域の近似品質をより細かく制御できます。阻止帯域に 1 の重み、通過帯域に 100 の重みを付けるようにフィルターを設計します。通過帯域の重みが大きいと、この領域での近似精度が高くなります。
Nb = 12; Na = 10; W = 1*(F<=0.5) + 100*(F>0.5); Hd = designfilt('arbmagnphaseiir',NumeratorOrder = Nb,DenominatorOrder=Na,Frequencies=F,... FrequencyResponse=H, DesignMethod='ls',Weights=W,SystemObject=true);
IIR 設計法を使用する場合、フィルターの安定性は保証されません。関数 isstable を使用して、IIR の安定性をチェックします。より徹底的な解析を行うには、極を確認し、それらがどれだけ単位円に近いかを調べます。
isstable(Hd)
ans = logical
1
IIR 設計応答をプロットします。通過帯域の近似は阻止帯域の近似より優れており、振幅ゲインが小さい (dB が低い) 場合は常に位相応答の重要性が低いことに注意してください。
FA = filterAnalyzer(Hd);
setLegendStrings(FA,"IIR Least-Squares")
figure [P,W] = phasez(Hd); plot(W/pi,P); hold on plot(F,unwrap(angle(H))+2*pi,'r--') hold off legend('IIR Least-Squares','Nominal Response', Location = 'NorthEast')

低い群遅延のバンドパス FIR 設計
任意の振幅と位相設計の応用として興味深いのは、小さい方の群遅延を優先して線形位相を放棄する非対称 FIR フィルターの設計です。このようなフィルターを設計すると、通過帯域で線形位相の近似を良好に保つことができます。バンドパス フィルターに、阻止帯域 と 、および通過帯域 の 3 つの帯域があるとします。通過帯域で、目的の周波数応答は で、これは群遅延を "gd" とする線形位相応答をもちます。
F1 = linspace(0,.25,30); % Lower stopband F2 = linspace(.3,.56,40); % Passband F3 = linspace(.62,1,30); % Higher stopband % Define the desired frequency response on the bands gd = 12; % Desired Group Delay P1 = zeros(size(F1)); P2 = exp(-1j*pi*F2*gd); P3 = zeros(size(F3)); F = [F1 F2 F3]; H = [P1 P2 P3];
目的の周波数応答をプロットします。
plotResponse(F, H)

FilterOrder = 50 および NumBands = 3 を指定し、さらに BandFrequencies ベクトルと BandFrequencyResponse ベクトルのペアを 3 つ指定して、3 つの帯域から成る任意応答 FIR フィルターを作成します。
N = 50; % Filter Order B = 3; % Number of bands Hd_mnp = designfilt('arbmagnphasefir',FilterOrder=N,NumBands=B,... BandFrequencies1=F1,BandFrequencyResponse1=P1,... BandFrequencies2=F2,BandFrequencyResponse2=P2,... BandFrequencies3=F3,BandFrequencyResponse3=P3,... DesignMethod='equiripple',SystemObject=true);
関数 islinphase を呼び出すとわかるように、この設計には線形位相がありません。
islinphase(Hd_mnp)
ans = logical
0
ここで、振幅応答のみを指定して任意の振幅フィルターを作成します。これは、designfilt の arbmagfir 応答を使用することで実行できます。BandFrequencies ベクトルと BandAmplitudes ベクトルのペアを使用して、必要な帯域周波数と振幅を指定します。arbmagnphasefir 応答と arbmagfir 応答の違いは、arbmagnphasefir の複素フィルター応答 BandFrequencyResponse が、arbmagfir では振幅のみ (非負の実数) の応答 BandAmplitudes に置き換えられていることです。
Hd_mo = designfilt('arbmagfir',FilterOrder=N,NumBands=B,... BandFrequencies1=F1,BandAmplitudes1=abs(P1),... BandFrequencies2=F2,BandAmplitudes2=abs(P2),... BandFrequencies3=F3,BandAmplitudes3=abs(P3),... DesignMethod='equiripple',SystemObject=true);
振幅のみの仕様では、線形位相をもつ対称設計が得られます。
islinphase(Hd_mo)
ans = logical
1
subplot(1,2,1); stem(Hd_mnp.Numerator) title('Magnitude and Phase Design (asymetric)') subplot(1,2,2); stem(Hd_mo.Numerator) title('Magnitude-only Design (symmetric)')

2 つの設計を比較します。両者のバンドパス振幅応答は非常に似通っていることに注意してください。
FA = filterAnalyzer(Hd_mnp, Hd_mo); setLegendStrings(FA,["Magnitude and Phase Design (Low Group Delay)", ... "Magnitude Only (Linear Phase, High Group Delay)"])

群遅延をプロットします。任意の振幅と位相設計では、群遅延が多少異なっています。ただし、差異は小さく、平均で 12.5 サンプルです。この群遅延は、振幅のみ設計の群遅延 (25 サンプル) の半分です。
FA = filterAnalyzer(Hd_mnp, Hd_mo,Analysis='groupdelay'); setLegendStrings(FA,["Magnitude and Phase Design (Low Group Delay)", ... "Magnitude Only (Linear Phase, High Group Delay)"]) zoom(FA,"xy",[0.3 0.56 0 35]);
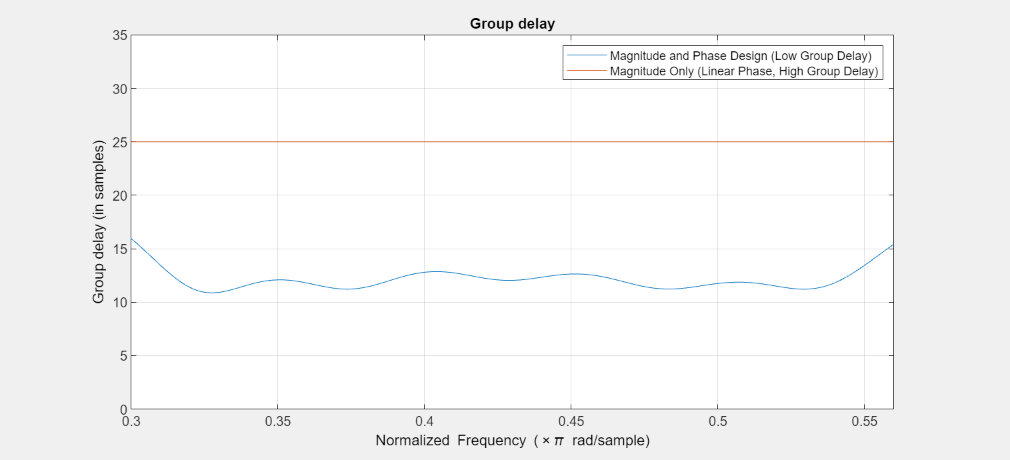
群遅延の違いは位相応答にも見られます。傾きが小さくなるほど、群遅延も小さくなることを示しています。
FA = filterAnalyzer(Hd_mnp, Hd_mo,Analysis='phase'); setLegendStrings(FA,["Magnitude and Phase Design (Low Group Delay)", ... "Magnitude Only (Linear Phase, High Group Delay)"]) zoom(FA,"xy",[0.3 0.56 -30 10]);

チェビシェフ ローパス フィルターの通過帯域のイコライズ
任意の振幅と位相設計の一般的な応用としては、他にも IIR フィルターの非線形位相応答のイコライズがあります。正規化された通過帯域周波数が 1/16 で、通過帯域リップルが 0.5 dB である 3 次のチェビシェフ タイプ I ローパス フィルターを考えます。
Fp = 1/16; % Passband frequency Ap = .5; % Passband ripples Hcheby = designfilt('lowpassiir',FilterOrder=3,PassbandFrequency=Fp,... PassbandRipple=Ap,DesignMethod='cheby1',SystemObject=true); FA = filterAnalyzer(Hcheby); setLegendStrings(FA, 'Chebyshev Lowpass');
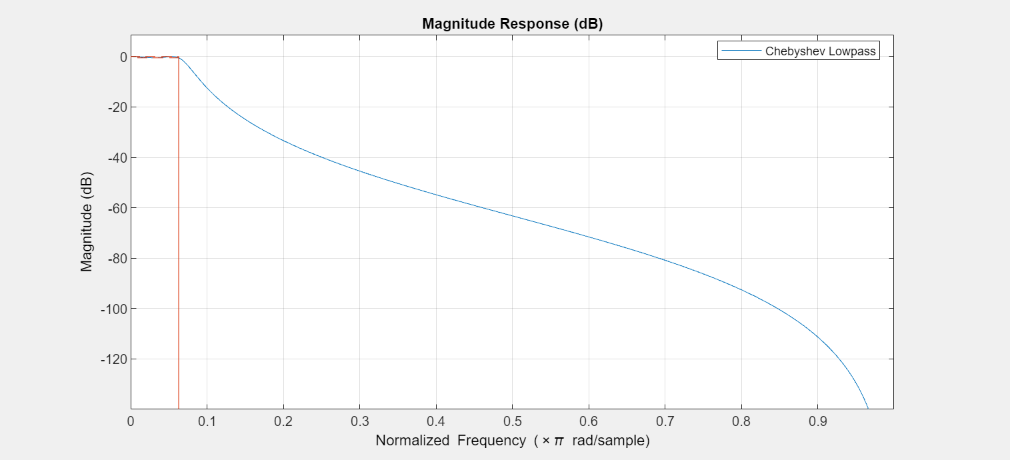
群遅延をプロットします。10 ~ 20 サンプルの範囲の群遅延をもつ通過帯域に、群遅延の大きな歪みがあります。
FA = filterAnalyzer(Hcheby, Analysis = 'groupdelay'); setLegendStrings(FA,'Chebyshev Lowpass');

群遅延の歪みを軽減する場合は、IIR フィルターの後に FIR イコライザー を使用します。理論的には、複合フィルターが理想的なローパスです。複合フィルターの通過帯域応答は であり、平坦な振幅応答および 個のサンプルの一定の群遅延に対する振幅リップルを除去します。対象群 は因果フィルター設計に割り当てられた FIR 長さに関連しています。この例では、 とするのが合理的な選択です。
要約すると、イコライザー設計には 2 つの帯域があります。
通過帯域では、イコライザーの目的となる周波数応答は となるはずです。
阻止帯域では、目的となる応答は となり、 と一致します。
この 2 帯域設計仕様によって、イコライザーの FIR 近似の焦点が通過帯域と阻止帯域にのみ当たるようになります。周波数領域の残りの部分は don't care 領域とみなされます。
gd = 35; % Passband Group Delay of the equalized filter (linear phase) F1 = 0:5e-4:Fp; % Passband D1 = exp(-1j*gd*pi*F1)./freqz(Hcheby,F1*pi); Fst = 3/16; % Stopband F2 = linspace(Fst,1,100); D2 = zeros(1,length(F2));
このイコライザー FIR 仕様の実装に使用できる FIR 設計法はいくつかあります。最小二乗設計と等リップル設計の 2 通りの設計法を使用してパフォーマンスを比較します。
Heq_ls = designfilt('arbmagnphasefir',FilterOrder=51,NumBands=2,... BandFrequencies1=F1,BandFrequencyResponse1=D1,... BandFrequencies2=F2,BandFrequencyResponse2=D2,... DesignMethod='ls',SystemObject=true); % Least-Squares design Heq_er = designfilt('arbmagnphasefir',FilterOrder=51,NumBands=2,... BandFrequencies1=F1,BandFrequencyResponse1=D1,... BandFrequencies2=F2,BandFrequencyResponse2=D2,... DesignMethod='equiripple',SystemObject=true); % Equiripple design % Create the cascaded filters Gls = cascade(Hcheby,Heq_ls); Geq = cascade(Hcheby,Heq_er);
両フィルターについてカスケード接続されたシステムの振幅応答をプロットします。
FA = filterAnalyzer(Hcheby,Gls,Geq); showFilters(FA,false,FilterNames = ["Gls_Stage1","Gls_Stage2","Geq_Stage1","Geq_Stage2"]) setLegendStrings(FA,["Chebyshev Lowpass (no equalization)","Least-Squares Equalization (cascade)", ... "Rquiripple Equalization (cascade)"]);

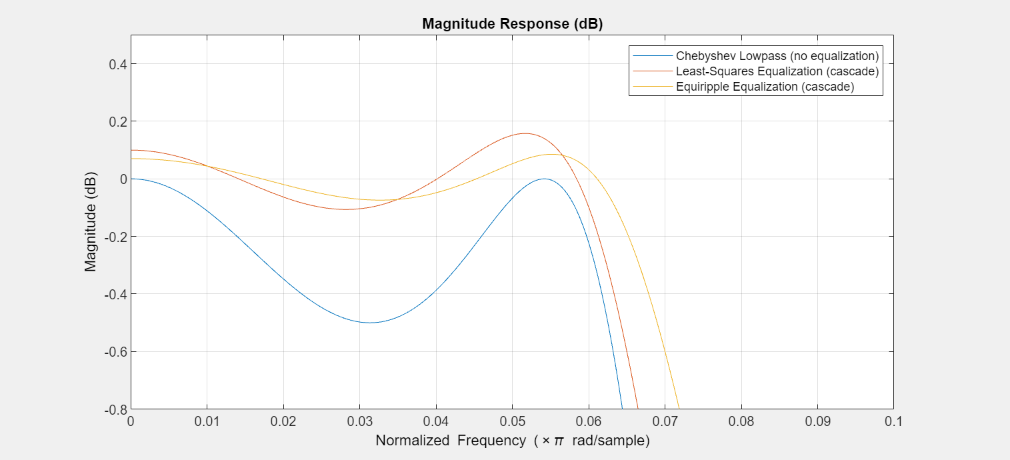
通過帯域付近をズームインします。イコライズの後、通過帯域リップルは最小二乗設計イコライザーの場合に元のフィルターの 0.5 dB から 0.27 dB に減衰し、等リップル設計イコライザーの場合は 0.16 dB に減衰します。
FA = filterAnalyzer(Hcheby,Gls,Geq); showFilters(FA,false,FilterNames = ["Gls_1_Stage1","Gls_1_Stage2","Geq_1_Stage1","Geq_1_Stage2"]) setLegendStrings(FA,["Chebyshev Lowpass (no equalization)", ... "Least-Squares Equalization (cascade)", ... "Equiripple Equalization (cascade)"]) zoom(FA,"xy",[0 .1 -0.8 .5]);
ここで、位相 (および群遅延) イコライズに目を向けます。複合群遅延は、通過帯域の 35 サンプル周辺 (対象群遅延) ではほぼ一定です。通過帯域外で複合群遅延が発散しているように見えますが、その領域ではフィルターのゲインがゼロになるため、これは重要ではありません。
FA = filterAnalyzer(Hcheby,Gls,Geq,Analysis='groupdelay'); showFilters(FA,false,FilterNames = ["Gls_2_Stage1","Gls_2_Stage2","Geq_2_Stage1","Geq_2_Stage2"]) setLegendStrings(FA,["Chebyshev Lowpass (no equalization)", ... "Least-Squares Equalization (cascade)", ... "Equiripple Equalization (cascade)"]) zoom(FA,"xy",[0 1 0 40]);
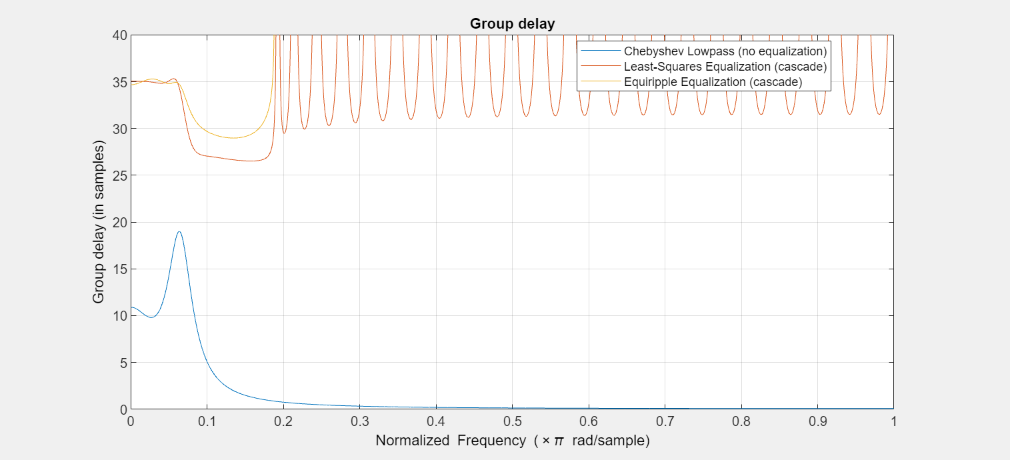
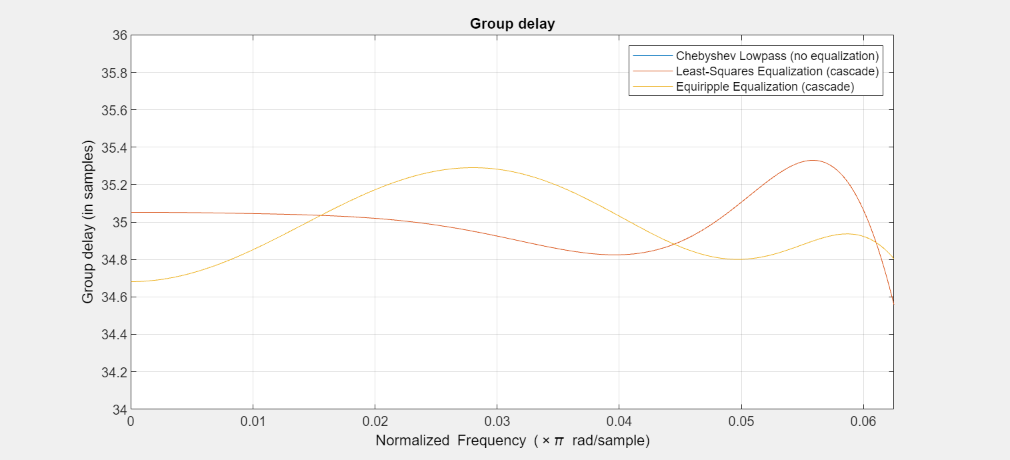
通過帯域付近をズームインします。通過帯域の群遅延は、8.8 サンプルのピーク ツー ピーク差から、最小二乗イコライザーで 0.51 サンプルにイコライズされ、等リップル イコライザーで 0.62 サンプルにイコライズされています。どちらのイコライザーも等しく良好に動作します。
FA = filterAnalyzer(Hcheby,Gls,Geq,Analysis='groupdelay'); showFilters(FA,false,FilterNames = ["Gls_3_Stage1","Gls_3_Stage2","Geq_3_Stage1","Geq_3_Stage2"]) setLegendStrings(FA,["Chebyshev Lowpass (no equalization)", ... "Least-Squares Equalization (cascade)", ... "Equiripple Equalization (cascade)"]) zoom(FA,"XY",[0 Fp 34 36]);
参照
[1] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989.