最小 p ノルム最適 FIR フィルターの設計

この例では、関数 firlpnorm を使用した最小 p ノルム FIR フィルターの設計法を示します。この関数は、制約なし最小 P 次最適化アルゴリズムを使用して、任意振幅応答をもつ FIR フィルターを設計します。

FIRLPNORM の構文

firlpnorm の構文は iirlpnorm と似ていますが (詳細については、最小 p ノルム最適 IIR フィルターの設計の例を参照)、分母の次数は指定しません。

この関数は、最小 P の最適 FIR フィルターを設計します。しかしながら、フィルターは線形位相をもつようには制約されません。つまり、インパルス応答には特別な対称プロパティはありません。

しかし、線形位相制約によって、さらに一般的な非線形位相設計よりも大きな次数をもつフィルターが設計されます。一部のハードウェア実装では、係数の対称性により、線形位相フィルターの実装時に乗数の数を半分に減らすことができる点に注意してください。たとえば、以下の firlpnorm 設計を考えます。

N = 30;
F = [0 0.3 0.45 1];
E = F;
A = [1 1 0 0];
W = [1 1 10 10];
b = firlpnorm(N,F,E,A,W);
hFiltAnalyzer = filterAnalyzer(b);

拡大すると、フィルターの通過帯域ピークリップルは約 0.008 で、阻止帯域ピークリップルは約 0.000832 であることがわかります。同等の仕様をもつ firpm または firgr 設計には 37 次のフィルターが必要です。firgr では仕様を満たす最小次数の線形位相 FIR フィルターがもたらされることを考えると、これは特に有意です。

dev = [0.008 0.000832];
bgr = firgr("minorder",F,A,dev);
orderfirgr = length(b)-1;
fprintf("Order: %d\n",orderfirgr);

Order: 30

hFiltAnalyzer.addFilters(bgr);
hFiltAnalyzer.setLegendStrings(["FIRLPNORM design" "FIRGR design"]);

もう 1 つの方法として、関数 firceqrip を使用することもできます。この関数も線形位相等リップルフィルターを設計しますが、仕様は firgr とは異なる方法で与えられます (詳細については、制約付き等リップル FIR フィルターの設計の例を参照してください)。firlpnorm による設計が達成できる通過帯域リップルと阻止帯域リップルを満たす 30 次の線形位相フィルターが必要な場合は、より大きな遷移幅を許容する必要があります。

bceq = firceqrip(30,(F(2)+F(3))/2,dev);
deleteFilters(hFiltAnalyzer, FilterNames="bgr");
addFilters(hFiltAnalyzer, bceq);
setLegendStrings(hFiltAnalyzer,["FIRLPNORM design","FIRCEQRIP design"]);

最小位相設計

もちろん、firgr で minphase オプションを指定することで、非線形位相フィルターを設計することもできます。それにより、必要な仕様を満たしながら、線形位相の場合よりも低い次数の FIR フィルターを得ることができます。ただしこの場合でも、結果は最適でない非線形位相フィルターになります。その理由は、次に示す例で明らかなように、仕様を満たす非線形位相等リップルフィルターに必要な最小次数よりもこのフィルターの次数が大きいためです。

bm = firgr("minorder",F,A,dev,"minphase");
orderfirgrmin = length(bm)-1;
fprintf("Order: %d\n",orderfirgrmin);

Order: 32

deleteFilters(hFiltAnalyzer, FilterNames="bceq");
addFilters(hFiltAnalyzer, bm);
setLegendStrings(hFiltAnalyzer,["FIRLPNORM design" "FIRGR minimum-phase design"]);

FIRLPNORM を使用した最小位相設計

firlpnorm では、ゼロが単位円上またはその内部に収まるように制約を課して、最小位相設計を得ることができます。ただしこの制約により、制約のない設計と比較して、通過帯域リップルが大きくなり、阻止帯域の減衰が小さくなります。

bmlp = firlpnorm(30,F,E,A,W,"minphase");
deleteFilters(hFiltAnalyzer, FilterNames="bm");
addFilters(hFiltAnalyzer, bmlp);
setLegendStrings(hFiltAnalyzer,["FIRLPNORM design" "FIRLPNORM minimum-phase design"]);

firgr を使用して設計した最小位相フィルターの次数と等しくなるように次数を増加すると、30 次の firlpnorm (非最小位相) 設計と 32 次の firgr 最小位相設計の両方によって満たされる仕様を満足できることがわかります。

bmlp = firlpnorm(orderfirgrmin,F,E,A,W,"minphase");
replaceFilters(hFiltAnalyzer, bmlp,FilterNames="bmlp");
addFilters(hFiltAnalyzer,bm);
setLegendStrings(hFiltAnalyzer,["FIRLPNORM design" "FIRLPNORM minimum-phase design" "FIRGR minimum-phase design"]);

p ノルムの変更

iirlpnorm や iirlpnormc と同様に、firlpnorm ではフィルターの最適化に使用される p ノルムの仕様を満たすことができます。p ノルムは iirlpnorm の場合とまったく同じ方法で指定します。つまり、Pinit と Pfinal を要素にもつ 2 要素のベクトルを使用します。Pinit はアルゴリズムによって使用される初期の p ノルムを指定し (収束を補佐するため)、Pfinal はフィルターが最適化される最終的な p ノルムを指定します。

たとえば、上記の仕様に対する最小二乗設計は、以下のようにして求めることができます。

N = 40;
F = [0 0.4 0.45 1];
E = F;
A = [0 0 1 1];
W = [1 1 10 10];
P = [2 2];
bl2 = firlpnorm(N,F,E,A,W,P);
addDisplays(hFiltAnalyzer,1);
addFilters(hFiltAnalyzer, bl2);
setLegendStrings(hFiltAnalyzer, "FIRLPNORM design");

FIRLS との比較

比較のために、firls を使用して線形位相最小二乗フィルターを設計します。ここでも、同じフィルター次数では、線形位相制約によって阻止帯域の減衰が少なくなり、通過帯域リップルが大きくなります。

W = [1 20];
bls = firls(N,F,A,W);
addFilters(hFiltAnalyzer,bls);
setLegendStrings(hFiltAnalyzer, ["FIRLPNORM design" "FIRLS design"]);

他のノルム

等リップル設計は、一連の設計の仕様を満たすために最小次数が必要な場合に役立ちます。最小二乗設計と同じ仕様を満たすには、より高い次数のフィルターが必要です。ただし、より高い次数では、阻止帯域 (通過帯域) のほとんどの部分において、余分な減衰 (より少ないリップル) がもたらされます。実のところ、最小二乗設計では阻止帯域のエネルギーが最小化されます。等リップル設計と最小二乗設計間の妥協は、中間ノルムを使用することで得ることができます。たとえば、同じ仕様をもちながら、次のノルムに対して最適化されたフィルターの設計は以下のようになります。2、4、12、256 (ほとんど無限のノルム)。

W = [1 1 10 10];
P4 = [2 4];
bl4 = firlpnorm(N,F,E,A,W,P4);
P12 = [2 12];
bl12 = firlpnorm(N,F,E,A,W,P12);
Pinf = [2 256];
blinf = firlpnorm(N,F,E,A,W,Pinf);
addDisplays(hFiltAnalyzer,1);
addFilters(hFiltAnalyzer,bl2,1,bl4,1,bl12,1,blinf,1);
setLegendStrings(hFiltAnalyzer, ["P = 2" "P = 4" "P = 12" "P = 256"]);

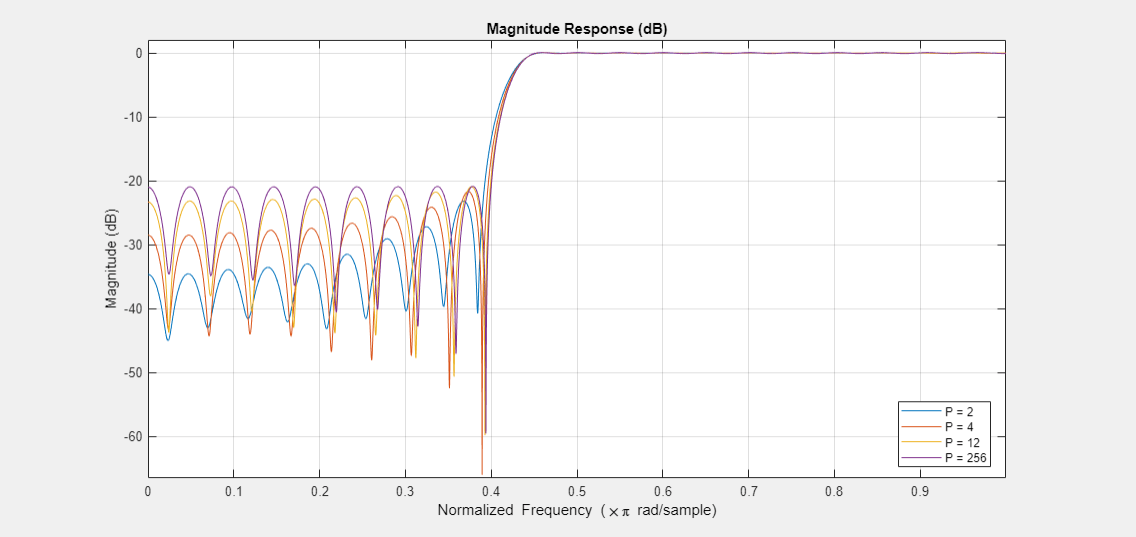
等リップル (256 ノルム) の場合の最小の阻止帯域の減衰を満たすには、他の設計の次数を増加する必要があります。