ローパス FIR フィルターの設計
この例では、fdesign を使用したローパス FIR フィルターの設計法を説明します。理想的なローパス フィルターは、無限インパルス応答を必要とします。インパルス応答の切り捨てまたはウィンドウ処理は、FIR フィルターの設計でウィンドウ法と呼ばれているものです。
さまざまなウィンドウを使用したローパス FIR フィルターの設計
FIR フィルターは、高性能な設計アルゴリズム、非再帰的な形で実装された際の安定性、線形位相の得やすさ、マルチレート ケースへの簡単な拡張性、充実したハードウェア サポートなどにより、広く使用されています。この例では、さまざまな特性のローパス FIR フィルターの設計に使用できる DSP System Toolbox™ の機能を紹介します。ここで説明する多くの概念は、ハイパス、バンドパスなどの他の応答にも拡張できます。
サンプルあたりのカットオフ周波数が 0.4*pi ラジアンであるシンプルなローパス フィルターの設計を考えます。
Fc = 0.4;
N = 100;
Hf = fdesign.lowpass('N,Fc',N,Fc);このローパス フィルターは、ウィンドウ法を使用して設計できます。たとえば、ハミング ウィンドウまたはドルフ・チェビシェフ ウィンドウを使用できます。
Hd1 = design(Hf,'window','window',@hamming,SystemObject=true); Hd2 = design(Hf,'window','window',{@chebwin,50}, ... SystemObject=true); filterAnalyzer(Hd1,Hd2,FilterNames=["HammingWindowDesign","DolphChebyshevWindowDesign"]);

どのようなフィルターを選択するかは自由です。理想的には次数を無限大にする必要があるため、一般に、大きい次数の方が理想の近似値になりますが、実装がコスト高になります。たとえば、ドルフ・チェビシェフ ウィンドウを使用する場合、次のようにしてフィルター次数を増やすことで遷移領域を減らすことができます。
Hf.FilterOrder = 200; Hd3 = design(Hf,'window','window',{@chebwin,50},... SystemObject=true); filterAnalyzer(Hd2,Hd3,FilterNames=["DolphChebyshevWindowDesignOrder100","DolphChebyshevWindowDesignOrder200"]);

最小次数ローパス フィルターの設計
適切なフィルター次数を判断するには、許容される通過帯域リップル量と阻止帯域の減衰量を指定する必要があります。また、理想的なカットオフ周波数付近における遷移領域の幅も指定する必要があります。後者については、通過帯域エッジ周波数と阻止帯域エッジ周波数を設定します。この 2 つの差によって、遷移幅が決定されます。
Fp = 0.38;
Fst = 0.42;
Ap = 0.06;
Ast = 60;
setspecs(Hf,'Fp,Fst,Ap,Ast',Fp,Fst,Ap,Ast);この場合も、ウィンドウ法とカイザー ウィンドウを使用してローパス フィルターを設計できます。
Hd4 = design(Hf,'kaiserwin',SystemObject=true);
measure(Hd4);ans =
Sampling Frequency : N/A (normalized frequency) Passband Edge : 0.38 3-dB Point : 0.39539 6-dB Point : 0.4 Stopband Edge : 0.42 Passband Ripple : 0.016058 dB Stopband Atten. : 60.092 dB Transition Width : 0.04
なお、指定した遷移幅は、カットオフ周波数 0.4 pi を中心とすることに注意してください。これは、ローパス フィルターのゲインが通過帯域のゲインの半分になる点 (または、フィルターの減衰量が 6 dB になる点) となります。
最適な最小次数設計
カイザー ウィンドウの設計は最適ではないため、この手法を使用した場合、仕様を満たすのに必要なフィルター次数が本来必要とされる次数よりも大きくなります。等リップル設計を使用すると、一連の仕様を満たすことができる最小次数のローパス フィルターを実現できます。
Hd5 = design(Hf,'equiripple',SystemObject=true); FA = filterAnalyzer(Hd4,Hd5,FilterNames=["KaiserWindowDesign","EquirippleDesign"]);
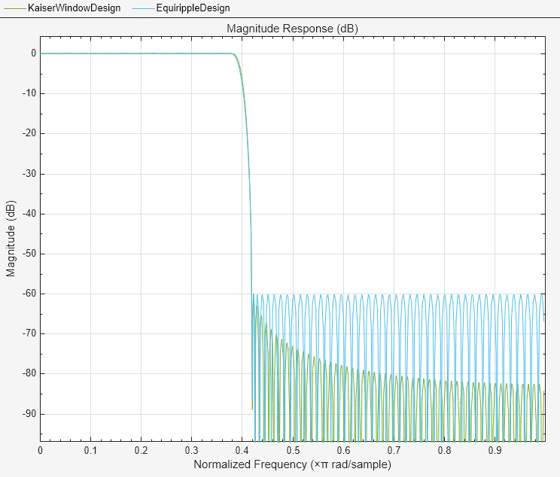
この場合、等リップル設計では 146 の係数が必要であるのに対し、カイザー ウィンドウ設計では 183 の係数が必要となります。
参考
fdesign | design | fdesign.lowpass | filterAnalyzer