Two-Channel Synthesis Subband Filter
Reconstruct signal from high-frequency and low-frequency subbands
Libraries:
DSP System Toolbox /
Filtering /
Multirate Filters
Description
The Two-Channel Synthesis Subband Filter block reconstructs a signal from its high-frequency and low-frequency subbands, each with half the bandwidth and half the sample rate of the original signal. Use this block to reconstruct signals decomposed by the Two-Channel Analysis Subband Filter block.
The block upsamples the high- and low-frequency subbands by 2, and then filters the results with a pair of highpass and lowpass FIR filters, as shown in this figure.

The block implements the FIR filtering and downsampling steps together using a polyphase filter structure, which is more efficient than the interpolate-then-filter algorithm shown in the preceding figure. You can implement a multilevel dyadic synthesis filter bank by connecting multiple copies of this block or by using the Dyadic Synthesis Filter Bank block. For more information, see Creating Multilevel Dyadic Synthesis Filter Banks.
You must provide a vector of filter coefficients for the lowpass and highpass FIR filters. Each filter should be a half-band filter that passes the frequency band that the other filter stops. You can use this block to reconstruct the output of a Two-Channel Analysis Subband Filter block. To do so, you must design the filters in this block such that they perfectly reconstruct the outputs of the analysis filters.
Ports
Input
Specify the high-frequency subband as a vector or a matrix. Both the high-frequency subband and the low-frequency subbands must have the same size and data type.
When the input is fixed-point, it must be signed only.
Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes
Specify the low-frequency subband as a vector or a matrix. Both the high-frequency subband and the low-frequency subbands must have the same size and data type.
If the input is fixed point, it must be a signed integer or a signed fixed point value with a power-of-two slope and zero bias.
Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes
Output
The block returns the synthesized output as a vector or a matrix. The number of rows in the output is the sum of the number of rows of the input signals.
Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes
Parameters
Main Tab
A vector of lowpass FIR filter coefficients, in descending powers of z. The lowpass filter should be a half-band filter that passes the frequency band stopped by the filter specified in the Highpass FIR filter coefficients parameter. To use this block to reconstruct the output of a Two-Channel Analysis Subband Filter block, you must design the filters in this block to perfectly reconstruct the outputs of the analysis filters. For more information, see Specify FIR Filters.
A vector of highpass FIR filter coefficients, in descending powers of z. The highpass filter should be a half-band filter that passes the frequency band stopped by the filter specified in the Lowpass FIR filter coefficients parameter. To use this block to reconstruct the output of a Two-Channel Analysis Subband Filter block, you must design the filters in this block to perfectly reconstruct the outputs of the analysis filters. For more information, see Specify FIR Filters.
Specify how the block should process the input. You can set this parameter to one of the following options:
Columns as channels (frame based)(default) — When you select this option, the block treats each column of the input as a separate channel.Elements as channels (sample based)— When you select this option, the block treats each element of the input as a separate channel.
For more information, see Frame-Based Processing and Sample-Based Processing.
Specify the rate processing rule for the block. You can set this parameter to one of the following options:
Enforce single-rate processing— When you select this option, the block treats each column of the input as an independent channel and reconstructs each channel over time. The output has the same sample rate as the input, but the output frame size is twice that of the input frame size. To select this option, you must set the Input processing parameter toColumns as channels (frame based).Allow multirate processing— When you select this option, the input and output of the block are the same size, but the sample rate of the output is twice that of the input.
Some settings of this parameter cause the block to have nonzero latency. See Latency for more information.
Data Types Tab
Select the rounding
mode for fixed-point operations. The filter coefficients do
not obey this parameter; they always round to
Nearest.
Note
The Rounding mode and Saturate on integer overflow settings have no effect on numerical results when all the following conditions exist:
Product output is
Inherit: Inherit via internal ruleAccumulator is
Inherit: Inherit via internal ruleOutput is
Inherit: Same as accumulator
With these data type settings, the block effectively operates in full-precision mode.
When you select this parameter, the block saturates the result of its
fixed-point operation. When you clear this parameter, the block wraps
the result of its fixed-point operation. For details on
saturate and wrap, see overflow
mode for fixed-point operations.
Note
The Rounding mode and Saturate on integer overflow parameters have no effect on numeric results when all these conditions are met:
Product output data type is
Inherit: Inherit via internal rule.Accumulator data type is
Inherit: Inherit via internal rule.
With these data type settings, the block operates in full-precision mode.
Specify the coefficients data type. See Fixed-Point Data Types and Multiplication Data Types for illustrations depicting the use of the coefficients data type in this block. You can set it to:
A rule that inherits a data type, for example,
Inherit: Same word length as inputAn expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the
Coefficients parameter.
to display the Data Type
Assistant, which helps you set the
Coefficients parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Specify the minimum value of the filter coefficients. The default value is
[] (unspecified). Simulink® software uses this value to perform automatic scaling of
fixed-point data types.
Specify the maximum value of the filter coefficients. The default value is
[] (unspecified). Simulink software uses this value to perform automatic scaling of
fixed-point data types.
Specify the product output data type. See Fixed-Point Data Types and Multiplication Data Types for illustrations depicting the use of the product output data type in this block. You can set it to:
A rule that inherits a data type, for example,
Inherit: Inherit via internal rule. For more information on this rule, see Inherit via Internal Rule.Note
The actual product output word length can be equal to or greater than the calculated ideal product output word length, depending on the settings on the Hardware Implementation pane of the Configuration Parameters dialog box.
An expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the Product
output parameter.
to display the Data Type
Assistant, which helps you set the Product
output parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Specify the accumulator data type. See Fixed-Point Data Types for illustrations depicting the use of the accumulator data type in this block. You can set this parameter to:
A rule that inherits a data type, for example,
Inherit: Inherit via internal rule. For more information on this rule, see Inherit via Internal Rule.An expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the
Accumulator parameter.
to display the Data Type
Assistant, which helps you set the
Accumulator parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Specify the output data type. See Fixed-Point Data Types for illustrations depicting the use of the output data type in this block. You can set it to:
A rule that inherits a data type, for example,
Inherit: Same as accumulatorAn expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the
Output parameter.
to display the Data Type
Assistant, which helps you set the
Output parameter.
See Control Data Types of Signals (Simulink) for more information.
Specify the minimum value that the block should output. The default
value is [] (unspecified). Simulink software uses this value to perform:
Simulation range checking (see Specify Signal Ranges (Simulink))
Automatic scaling of fixed-point data types
Specify the maximum value that the block should output. The default
value is [] (unspecified). Simulink software uses this value to perform:
Simulation range checking (see Specify Signal Ranges (Simulink))
Automatic scaling of fixed-point data types
Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
You must provide the vector of numerator coefficients for the lowpass and highpass filters in the Lowpass FIR filter coefficients and Highpass FIR filter coefficients parameters.
For example, to specify a filter with the following transfer function, enter the
vector [b(1) b(2) ... b(m)].
Each filter should be a half-band filter that passes the frequency band that the other filter stops. You can use this block to reconstruct the output of a Two-Channel Analysis Subband Filter block. To do so, you must design the filters in this block such that they perfectly reconstruct the outputs of the analysis filters.
The best way to design perfect reconstruction filters is to use the Wavelet Toolbox™
wfilters function for the filters in both this block
and in the corresponding Two-Channel Analysis
Subband Filter block. You can also use DSP System Toolbox™ and Signal Processing Toolbox™ functions.
The Two-Channel Synthesis Subband Filter block initializes all filter states to zero.
When you set the Input processing parameter to
Columns as channels (frame based), the block accepts
any two M-by-N matrices with the same frame
rates. The block treats each column of the input as the high- or low-frequency
subbands of the corresponding output channel. You can use the Rate
options parameter to specify how the block resamples the
input:
When you set the Rate options parameter to
Enforce single-rate processing, the input to the block can be any two M-by-N matrices with the same frame rate. The block treats each input column as the high- or low-frequency subbands of the corresponding output channel. The input to the topmost input port should contain the high-frequency subbands. The block outputs one matrix, where each column is reconstructed from the corresponding columns of each input matrix. The input and output frame rates are the same, but the frame size of the output is twice that of the input.When you set the Rate options parameter to
Allow multirate processing, the block treats each column of the input as the high- or low-frequency subbands of the corresponding output channel. The input to the topmost input port should contain the high-frequency subbands. The block outputs one matrix, where each column is reconstructed from the corresponding columns of the input matrices. The input and output frame sizes are the same, but the frame rate of the output is twice that of the input. Thus, the overall sample rate of the output is twice that of the input sample rate.In this mode, the block has one frame of latency, as described in the Latency section.
When you set the Input processing parameter to
Elements as channels (sample based), the block
accepts any two M-by-N matrices with the same
sample rates. The block treats each M-by-N
matrix as M · N independent subbands. Each element of the input matrices is the
high- or low-frequency subband of the corresponding channel in the output matrix.
The input to the topmost input port should contain the high-frequency subbands. The
block outputs one matrix with the same dimensions as the input matrices, but a
sample rate that is twice that of the input. The block reconstructs each element of
the output from the corresponding elements in the input matrices.
Depending on the setting of your Simulink configuration parameters, the output may have one sample of latency, as described in the Latency section.
When you set the Input processing parameter to
Columns as channels (frame based) and the
Rate options parameter to Enforce single-rate
processing, the Two-Channel Synthesis Subband
Filter block always has zero-tasking latency. Zero-tasking
latency means that the block propagates the first input sample
(received at time t= 0) as the first output sample.
When you set the Rate options parameter to Allow
multirate processing, the Two-Channel Synthesis Subband
Filter block may exhibit latency. The amount of latency depends on the
setting of the Input processing parameter of this block and the
setting of the Simulink
Treat each discrete rate as a separate task configuration
parameter. The following table summarizes the conditions that produce latency when
the block is performing multirate processing.
| Input processing | Treat each discrete rate as a separate task | Latency |
|---|---|---|
|
Off
| None. |
On
| One sample. The first output sample in each channel always
has a value of | |
|
Off or On
| One frame. All samples in the first output frame have a
value of |
Note
For more information on latency and the Simulink tasking modes, see Excess Algorithmic Delay (Tasking Latency) and Time-Based Scheduling and Code Generation (Simulink Coder).
The Two-Channel Synthesis Subband Filter block is the basic unit of a dyadic synthesis filter bank. You can connect several of these blocks to implement an n-level filter bank, as illustrated in the following figure. For a review of dyadic synthesis filter banks, see the Dyadic Synthesis Filter Bank block reference page.
When you create a filter bank by connecting multiple copies of this block, the output values of the filter bank differ depending on whether there is latency. Though the output values differ, both sets of values are valid; the difference arises from changes in latency. See the Latency section for more information about when latency can occur in the Two-Channel Analysis Subband Filter block.
In some cases, rather than connecting several Two-Channel Analysis Subband Filter blocks, you can use the Dyadic Analysis Filter Bank block, which is faster and requires lesser memory. In particular, the Dyadic Analysis Filter Bank block is more efficient under the following conditions:
You are reconstructing a signal from 2n or n+ 1 subbands.
The frame size of the signal you are reconstructing is a multiple of 2n.
The properties of the subbands you are working with match those of the outputs of the Dyadic Analysis Filter Bank block. These properties are described in the Dyadic Analysis Filter Bank reference page.

The Dyadic Synthesis Filter Bank block allows you to specify the filter bank filters by providing vectors of filter coefficients, just as this block does. The Dyadic Synthesis Filter Bank block provides an additional option of using wavelet-based filters that the block designs by using a wavelet you specify.
Fixed-point data types in the Two-Channel Synthesis Subband Filter block.
The Two-Channel Synthesis Subband Filter block is composed of two FIR Interpolation blocks as shown in the following diagram.
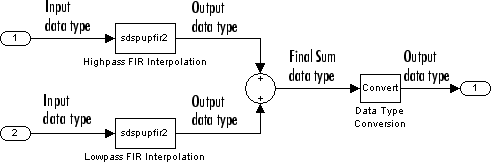
For fixed-point signals, you can set the coefficient, product output, accumulator, and output data types used in the FIR Interpolation blocks as discussed in Parameters. For a diagram showing the usage of these data types within the FIR blocks, see the FIR Interpolation block reference page.
In addition, the inputs to the Sum (Simulink) block shown in the previous diagram are accumulated using the accumulator data type. The output of the Sum block is then cast from the accumulator data type to the output data type. Therefore the output of the Two-Channel Synthesis Subband Filter block is in the output data type. You also set these data types in the block dialog box as discussed in the Parameters section.
If the input is fixed point, it must be a signed integer or a signed fixed point value with a power-of-two slope and zero bias.
References
[1] Fliege, N. J. Multirate Digital Signal Processing: Multirate Systems, Filter Banks, Wavelets. West Sussex, England: John Wiley & Sons, 1994.
[2] Strang, G. and T. Nguyen. Wavelets and Filter Banks. Wellesley, MA: Wellesley-Cambridge Press, 1996.
[3] Vaidyanathan, P. P. Multirate Systems and Filter Banks. Englewood Cliffs, NJ: Prentice Hall, 1993.
Extended Capabilities
Generated code relies on the memcpy or
memset function (string.h) under certain
conditions.
Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.
Version History
Introduced before R2006a
See Also
Functions
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)