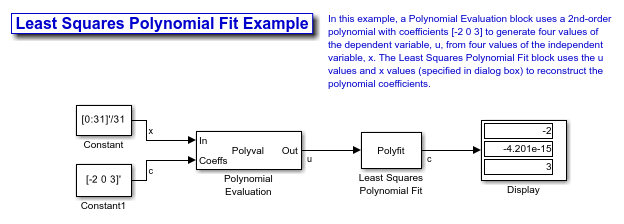
Least Squares Polynomial Fit

最小二乗法を使用して入力データに最も適合する多項式係数を計算する

• 

ライブラリ:
DSP System Toolbox / Math Functions / Polynomial Functions

説明

Least Squares Polynomial Fit ブロックは、最小二乗法を使用して入力データに最も適合する n 次多項式の係数を計算します。ここで、n は [多項式の次数] パラメーターで指定する値です。このブロックは、M 行 N 列の入力 u の各列について、n+1 個の係数の組をそれぞれ計算します。

例

Least Squares Polynomial Fit ブロックを使用した多項式係数の計算

ex_leastsquarespolyfit_ref モデルを開きます。Polynomial Evaluation ブロックは、次の 2 次多項式を使用して、In 端子で受信した独立変数 u の 4 つの値から従属変数 y の 4 つの値を生成します。

多項式係数はベクトル [-2 0 3] で Coeffs 端子に供給されます。1 次項の係数はゼロであることに注意してください。

Least Squares Polynomial Fit ブロックの [制御点] パラメーターは、Polynomial Evaluation ブロックへの入力として使用される独立変数 u の同じ 4 つの値 [1 2 3 4] で構成されます。Least Squares Polynomial Fit ブロックは、それらの値を従属変数 y の入力値と組み合わせて使用し、元の多項式係数を再構築します。

端子

入力

Input — 入力データ

ベクトル | 行列

入力データを M 行 N 列のベクトルまたは行列として指定します。ブロックは、長さが M の方向性をもたないベクトル入力を M 行 1 列の行列として扱います。

データ型: single | double

出力

Output — 多項式係数

列ベクトル | 行列

最小二乗法で入力データに最も適合する多項式係数。列ベクトルまたは (n+1) 行 N 列のサイズの行列として返されます。ここで、n は [多項式の次数] パラメーターで指定する値です。

(n+1) 行 N 列の出力行列 c の各列は、入力の対応する列に最も適合する多項式を記述する n+1 個の係数の組を表します。各列の係数は指数が降順となるように配置されます (c₁、c₂、...、c_n+1)。

このブロックが多項式係数を計算する方法の詳細については、アルゴリズムを参照してください。

データ型: single | double

パラメーター

制御点 (X) — 制御点

(0:31)/31 (既定値) | ベクトル

各入力列のデータに対応する独立変数の値を指定します。M 行 N 列の入力の場合、このパラメーターは長さ M のベクトルでなければなりません。

調整可能: Yes

多項式の次数 (N) — 多項式の次数

3 (既定値) | 正の整数

ブロックが最適な近似を構成するために使用する多項式の次数 n を指定します。係数の数は n+1 です。

ブロックの特性

データ型	double | single
直達	なし
多次元信号	なし
可変サイズの信号	なし
ゼロクロッシング検出	なし

アルゴリズム

指定された入力列に対して、ブロックは係数のセット c₁、c₂、...、c_n+1 を計算し、量 $${\displaystyle \sum _{i=1}^M{(u_i-{\widehat{u}}_i)}^2}$$ を最小化します。ここで、u_i は入力列の i 番目の要素であり、次のようになります。

$${\widehat{u}}_i=f\left(x_i\right)=c_1{x}_i^n+c_2{x}_i^{n-1}+\mathrm{...}+c_{n+1}.$$

独立変数 x₁、x₂、...、x_M の値は、[制御点] パラメーターによって長さ M のベクトルとして指定されます。N 個のすべての多項式近似で M 個の同じ制御点が使用されます。ただし、それらは等間隔であるとは限りません。

相当する MATLAB^® コードを以下に示します。

c = polyfit(x,u,n)

拡張機能

C/C++ コード生成

Simulink® Coder™ を使用して C および C++ コードを生成します。

生成されたコードは特定の条件下で関数 memcpy または関数 memset (string.h) に依存します。

バージョン履歴

R2006a より前に導入

参考

関数

• polyfit

ブロック

• Detrend | Polynomial Evaluation | Polynomial Stability Test