Physics Informed Neural Network を使用した PDE の求解

この例では次を使用します。

この例では、Physics Informed Neural Network (PINN) に学習させて偏微分方程式 (PDE) の解を予測する方法を示します。

Physics Informed Neural Network (PINN) [1] は、構造と学習プロセスに物理法則を組み込んだニューラルネットワークです。たとえば、物理システムを定義する PDE の解を出力するニューラルネットワークに学習させることができます。

この例では、サンプル $(x, t)$ を入力として受け取って $u (x, t)$ を出力する PINN に学習させます。ここで、 $u$ は次のバーガース方程式の解です。

$\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} - \frac{0.01}{π} \frac{\partial^{2} u}{\partial x^{2}} = 0,$

初期状態は $u (x, 0) = - s i n (π x)$ 、境界条件は $u (- 1, t) = 0$ および $u (1, t) = 0$ とします。

次の図は、PINN を通るデータの流れを示しています。

Diagram of the data flow of the neural network. The input is x_1, x_2, ... x_N, and t. The output is the PDE solution u(x,t).

このモデルの学習には、事前のデータ収集を必要としません。PDE の定義および制約を使用して、データを生成できます。

学習データの生成

モデルに学習させるには、境界条件を強制し、初期状態を強制し、バーガース方程式を満たす選点のデータセットが必要です。

25 個の等間隔の時間点を選択して、各境界条件 $u (- 1, t) = 0$ および $u (1, t) = 0$ を強制します。

numBoundaryConditionPoints = [25 25];

x0BC1 = -1*ones(1,numBoundaryConditionPoints(1));
x0BC2 = ones(1,numBoundaryConditionPoints(2));

t0BC1 = linspace(0,1,numBoundaryConditionPoints(1));
t0BC2 = linspace(0,1,numBoundaryConditionPoints(2));

u0BC1 = zeros(1,numBoundaryConditionPoints(1));
u0BC2 = zeros(1,numBoundaryConditionPoints(2));

50 個の等間隔の時間点を選択して、初期状態 $u (x, 0) = - s i n (π x)$ を強制します。

numInitialConditionPoints  = 50;

x0IC = linspace(-1,1,numInitialConditionPoints);
t0IC = zeros(1,numInitialConditionPoints);
u0IC = -sin(pi*x0IC);

初期状態および境界条件について、データをグループ化します。

X0 = [x0IC x0BC1 x0BC2];
T0 = [t0IC t0BC1 t0BC2];
U0 = [u0IC u0BC1 u0BC2];

10,000 個の点 $(t, x) \in (0, 1) \times (- 1, 1)$ を均等にサンプリングし、ネットワークの出力がバーガース方程式を満たすように強制します。

numInternalCollocationPoints = 10000;

points = rand(numInternalCollocationPoints,2);

dataX = 2*points(:,1)-1;
dataT = points(:,2);

ニューラルネットワークアーキテクチャの定義

多層パーセプトロンニューラルネットワークアーキテクチャを定義します。

Diagram of the neual network architecture. The layers are connected in series. The input is passed through 8 fully connected layers that are each proceeded by a tanh layer. The output of the final tanh layer is connected to a fully connected layer, which outputs the network predictions.

繰り返し現れる全結合層では、出力サイズを 20 に指定します。
最後の全結合層では、出力サイズを 1 に指定します。

ネットワークのハイパーパラメーターを指定します。

numBlocks = 8;
fcOutputSize = 20;

ニューラルネットワークを作成します。層のブロックを繰り返してニューラルネットワークを簡単に構築するには、repmat 関数を使用して層のブロックを繰り返します。

fcBlock = [
    fullyConnectedLayer(fcOutputSize)
    tanhLayer];

layers = [
    featureInputLayer(2)
    repmat(fcBlock,[numBlocks 1])
    fullyConnectedLayer(1)]

layers = 
  18×1 Layer array with layers:

     1   ''   Feature Input     2 features
     2   ''   Fully Connected   20 fully connected layer
     3   ''   Tanh              Hyperbolic tangent
     4   ''   Fully Connected   20 fully connected layer
     5   ''   Tanh              Hyperbolic tangent
     6   ''   Fully Connected   20 fully connected layer
     7   ''   Tanh              Hyperbolic tangent
     8   ''   Fully Connected   20 fully connected layer
     9   ''   Tanh              Hyperbolic tangent
    10   ''   Fully Connected   20 fully connected layer
    11   ''   Tanh              Hyperbolic tangent
    12   ''   Fully Connected   20 fully connected layer
    13   ''   Tanh              Hyperbolic tangent
    14   ''   Fully Connected   20 fully connected layer
    15   ''   Tanh              Hyperbolic tangent
    16   ''   Fully Connected   20 fully connected layer
    17   ''   Tanh              Hyperbolic tangent
    18   ''   Fully Connected   1 fully connected layer

層配列を dlnetwork オブジェクトに変換します。

net = dlnetwork(layers)

net = 
  dlnetwork with properties:

         Layers: [18×1 nnet.cnn.layer.Layer]
    Connections: [17×2 table]
     Learnables: [18×3 table]
          State: [0×3 table]
     InputNames: {'input'}
    OutputNames: {'fc_9'}
    Initialized: 1

  View summary with summary.

学習可能なパラメーターのデータ型が double である場合、PINN の学習の精度が向上します。関数 dlupdate を使用して、ネットワークの学習可能なパラメーターを double に変換します。たとえば single 型の学習可能なパラメーターに依存する GPU 最適化を使用するネットワークなど、すべてのニューラルネットワークが double 型の学習可能なパラメーターをサポートしているわけではないことに注意してください。

net = dlupdate(@double,net);

モデル損失関数の定義

ニューラルネットワーク、ネットワーク入力、初期条件と境界条件を入力として受け取り、学習可能なパラメーターについての損失の勾配、および対応する損失を返す関数 modelLoss を作成します。

与えられた入力 $(x, t)$ について、ネットワークの出力 $u (x, t)$ がバーガース方程式、境界条件、および初期状態を満たすように強制することで、モデルに学習させます。特に、次の 2 つの量が損失の最小化に寄与します。

$loss = {MSE}_{f} + {MSE}_{u}$ ,

ここで、 ${MSE}_{f} = \frac{1}{N_{f}} \sum_{i = 1}^{N_{f}} {| f (x_{f}^{i}, t_{f}^{i}) |}^{2}$ 、 ${MSE}_{u} = \frac{1}{N_{u}} \sum_{i = 1}^{N_{u}} {| u (x_{u}^{i}, t_{u}^{i}) - u^{i} |}^{2}$ です。関数 $f$ はバーガース方程式の左辺です。 ${x_{u}^{i}, t_{u}^{i}}_{i = 1}^{N_{u}}$ は計算領域の境界上の選点に対応し、境界条件と初期状態の両方が考慮されています。 ${x_{f}^{i}, t_{f}^{i}}_{i = 1}^{N_{f}}$ は領域内部の点です。

function [loss,gradients] = modelLoss(net,X,T,X0,T0,U0)

% Make predictions with the initial conditions.
XT = cat(1,X,T);
U = forward(net,XT);

% Calculate derivatives with respect to X and T.
X = stripdims(X);
T = stripdims(T);
U = stripdims(U);
Ux = dljacobian(U,X,1);
Ut = dljacobian(U,T,1);

% Calculate second-order derivatives with respect to X.
Uxx = dldivergence(Ux,X,1);

% Calculate mseF. Enforce Burger's equation.
f = Ut + U.*Ux - (0.01./pi).*Uxx;
mseF = mean(f.^2);

% Calculate mseU. Enforce initial and boundary conditions.
XT0 = cat(1,X0,T0);
U0Pred = forward(net,XT0);
mseU = l2loss(U0Pred,U0);

% Calculated loss to be minimized by combining errors.
loss = mseF + mseU;

% Calculate gradients with respect to the learnable parameters.
gradients = dlgradient(loss,net.Learnables);

end

学習オプションの指定

学習オプションを指定します。

L-BFGS ソルバーを使用して学習させ、L-BFGS ソルバーの状態に対して既定のオプションを使用する。
1500 回反復して学習させる
勾配またはステップのノルムが $1 0^{- 5}$ より小さい場合は、学習を早期に停止する。

solverState = lbfgsState;
maxIterations = 1500;
gradientTolerance = 1e-5;
stepTolerance = 1e-5;

ニューラルネットワークの学習

学習データを dlarray オブジェクトに変換します。入力 X および T の形式を "BC" (batch、channel) と指定し、初期状態の形式を "CB" (channel、batch) と指定します。

X = dlarray(dataX,"BC");
T = dlarray(dataT,"BC");
X0 = dlarray(X0,"CB");
T0 = dlarray(T0,"CB");
U0 = dlarray(U0,"CB");

dlaccelerate関数を使用して、損失関数を高速化します。関数の高速化の詳細については、Deep Learning Function Acceleration for Custom Training Loopsを参照してください。

accfun = dlaccelerate(@modelLoss);

L-BFGS の更新ステップに関する損失関数を含む関数ハンドルを作成します。自動微分を使用して関数 modelLoss 内で関数 dlgradient を評価するには、関数 dlfeval を使用します。

lossFcn = @(net) dlfeval(accfun,net,X,T,X0,T0,U0);

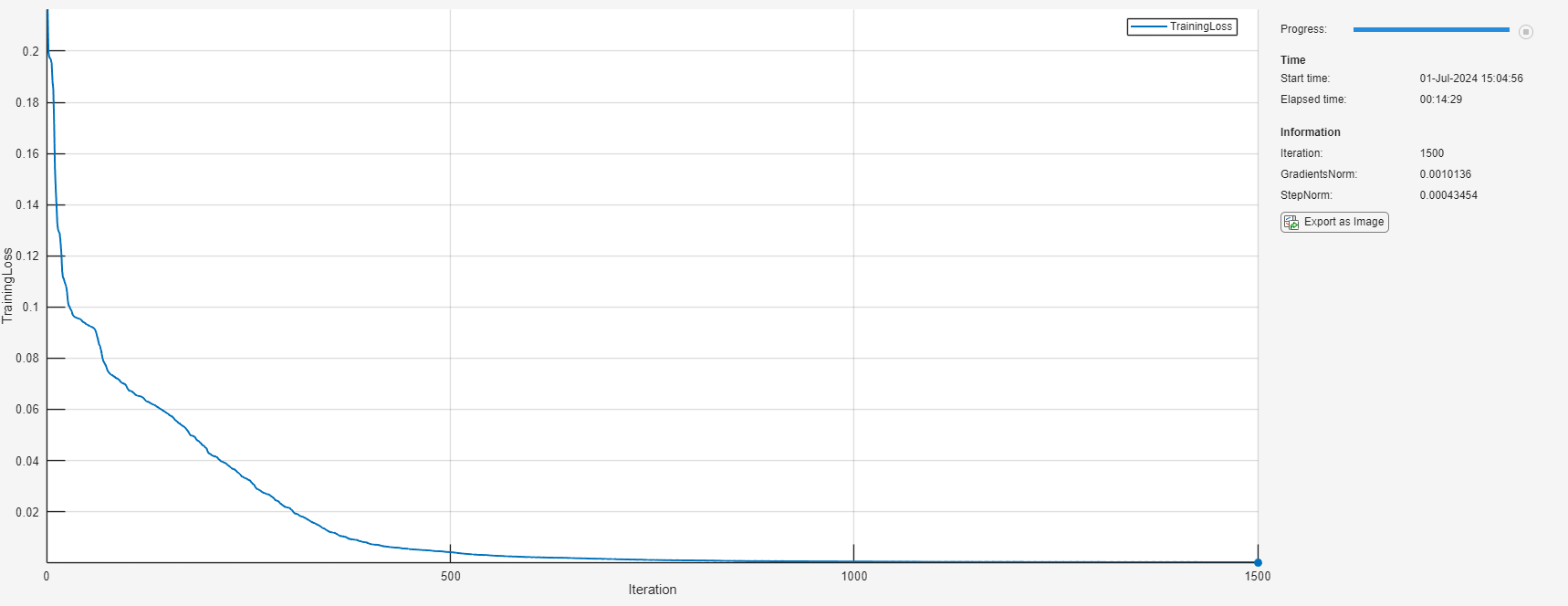
TrainingProgressMonitor オブジェクトを初期化します。各反復で損失をプロットし、勾配とステップのノルムを監視します。監視オブジェクトを作成するとタイマーが開始されるため、学習ループに近いところでオブジェクトを作成するようにしてください。

monitor = trainingProgressMonitor( ...
    Metrics="TrainingLoss", ...
    Info=["Iteration" "GradientsNorm" "StepNorm"], ...
    XLabel="Iteration");

各反復でデータセット全体を使用し、カスタム学習ループを使用してネットワークに学習させます。それぞれの反復で次を行います。

関数 lbfgsupdate を使用して、ネットワークの学習可能なパラメーターとソルバーの状態を更新します。
学習の進行状況モニターを更新します。
勾配のノルムが指定された許容値を下回る場合、または直線探索が失敗した場合は、学習を早期に停止します。

iteration = 0;
while iteration < maxIterations && ~monitor.Stop
    iteration = iteration + 1;
    [net, solverState] = lbfgsupdate(net,lossFcn,solverState);

    updateInfo(monitor, ...
        Iteration=iteration, ...
        GradientsNorm=solverState.GradientsNorm, ...
        StepNorm=solverState.StepNorm);

    recordMetrics(monitor,iteration,TrainingLoss=solverState.Loss);

    monitor.Progress = 100*iteration/maxIterations;

    if solverState.GradientsNorm < gradientTolerance || ...
            solverState.StepNorm < stepTolerance || ...
            solverState.LineSearchStatus == "failed"
        break
    end

end

モデルの精度の評価

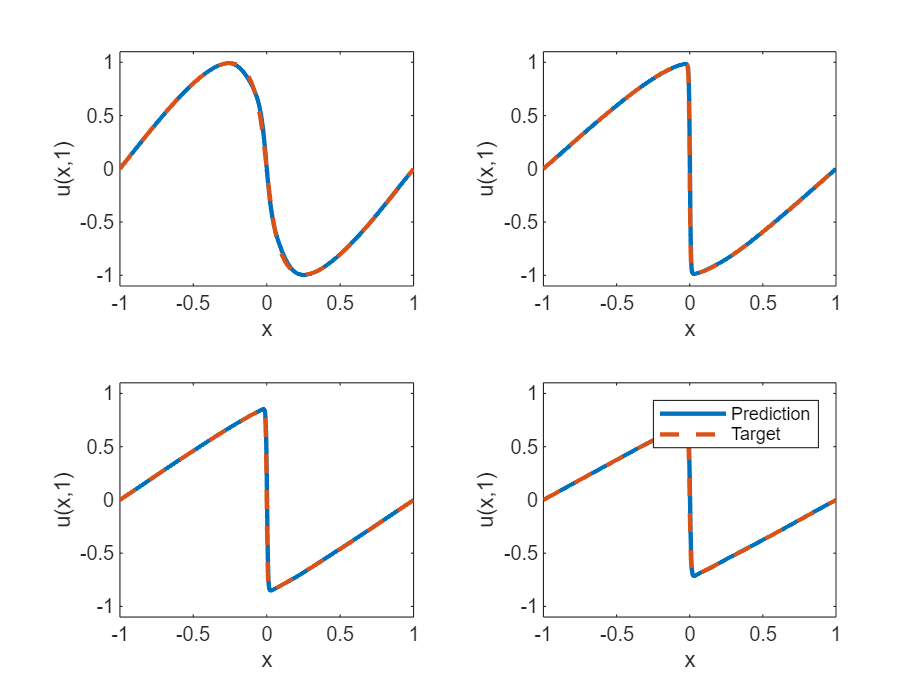
$t$ の値が 0.25、0.5、0.75、および 1 である場合について、深層学習モデルの予測値とバーガース方程式の真の解を比較します。

モデルをテストする際のターゲット時間を設定します。各時間について、[-1,1] の範囲内の 1001 個の等間隔の点で解を計算します。

tTest = [0.25 0.5 0.75 1];
numObservationsTest = numel(tTest);

szXTest = 1001;
XTest = linspace(-1,1,szXTest);
XTest = dlarray(XTest,"CB");

モデルをテストします。各テスト入力について、PINN を使用して PDE の解を予測し、この例のバーガース方程式の求解関数セクションにリストされている solveBurgers 関数によって与えられた解と比較します。この関数にアクセスするには、例をライブスクリプトとして開きます。予測とターゲットとの間の相対誤差を計算して精度を評価します。

UPred = zeros(numObservationsTest,szXTest);
UTest = zeros(numObservationsTest,szXTest);

for i = 1:numObservationsTest
    t = tTest(i);

    TTest = repmat(t,[1 szXTest]);
    TTest = dlarray(TTest,"CB");
    XTTest = cat(1,XTest,TTest);

    UPred(i,:) = forward(net,XTTest);
    UTest(i,:) = solveBurgers(extractdata(XTest),t,0.01/pi);
end

err = norm(UPred - UTest) / norm(UTest)

err = 
0.0237

テストの予測をプロットで可視化します。

figure
tiledlayout("flow")

for i = 1:numel(tTest)
    nexttile
    
    plot(XTest,UPred(i,:),"-",LineWidth=2);

    hold on
    plot(XTest, UTest(i,:),"--",LineWidth=2)
    hold off

    ylim([-1.1, 1.1])
    xlabel("x")
    ylabel("u(x," + t + ")")
end

legend(["Prediction" "Target"])

バーガース方程式の求解関数

solveBurgers 関数は、[2] で概説されているように、時間 t におけるバーガース方程式の真の解を返します。

function U = solveBurgers(X,t,nu)

% Define functions.
f = @(y) exp(-cos(pi*y)/(2*pi*nu));
g = @(y) exp(-(y.^2)/(4*nu*t));

% Initialize solutions.
U = zeros(size(X));

% Loop over x values.
for i = 1:numel(X)
    x = X(i);

    % Calculate the solutions using the integral function. The boundary
    % conditions in x = -1 and x = 1 are known, so leave 0 as they are
    % given by initialization of U.
    if abs(x) ~= 1
        fun = @(eta) sin(pi*(x-eta)) .* f(x-eta) .* g(eta);
        uxt = -integral(fun,-inf,inf);
        fun = @(eta) f(x-eta) .* g(eta);
        U(i) = uxt / integral(fun,-inf,inf);
    end
end

end

参考文献

Maziar Raissi, Paris Perdikaris, and George Em Karniadakis, Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations https://arxiv.org/abs/1711.10561
C. Basdevant, M. Deville, P. Haldenwang, J. Lacroix, J. Ouazzani, R. Peyret, P. Orlandi, A. Patera, Spectral and finite difference solutions of the Burgers equation, Computers & fluids 14 (1986) 23–41.

参考

dlarray | dlfeval | dlgradient