resnetNetwork
Description
net = resnetNetwork(inputSize,numClasses)
To create a 3-D residual network, use resnet3dNetwork.
net = resnetNetwork(inputSize,numClasses,Name=Value)BottleneckType="none" returns a 2-D residual neural network without
bottleneck components.
Tip
To load a pretrained ResNet neural network, use the imagePretrainedNetwork function.
Examples
Create a residual network with a bottleneck architecture.
imageSize = [224 224 3]; numClasses = 10; net = resnetNetwork(imageSize,numClasses)
net =
dlnetwork with properties:
Layers: [176×1 nnet.cnn.layer.Layer]
Connections: [191×2 table]
Learnables: [214×3 table]
State: [106×3 table]
InputNames: {'input'}
OutputNames: {'softmax'}
Initialized: 1
View summary with summary.
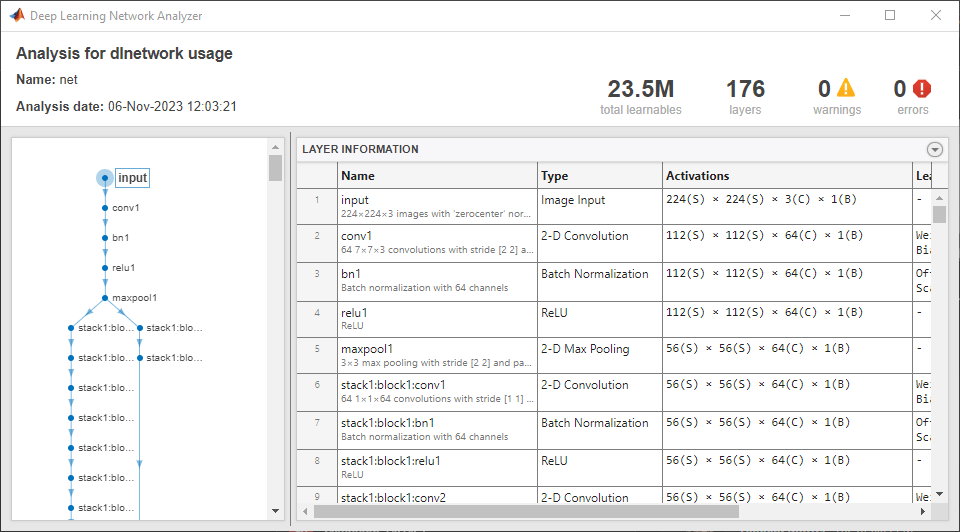
Analyze the network using the analyzeNetwork function. Note that this network is equivalent to a ResNet-50 residual neural network.
analyzeNetwork(net)
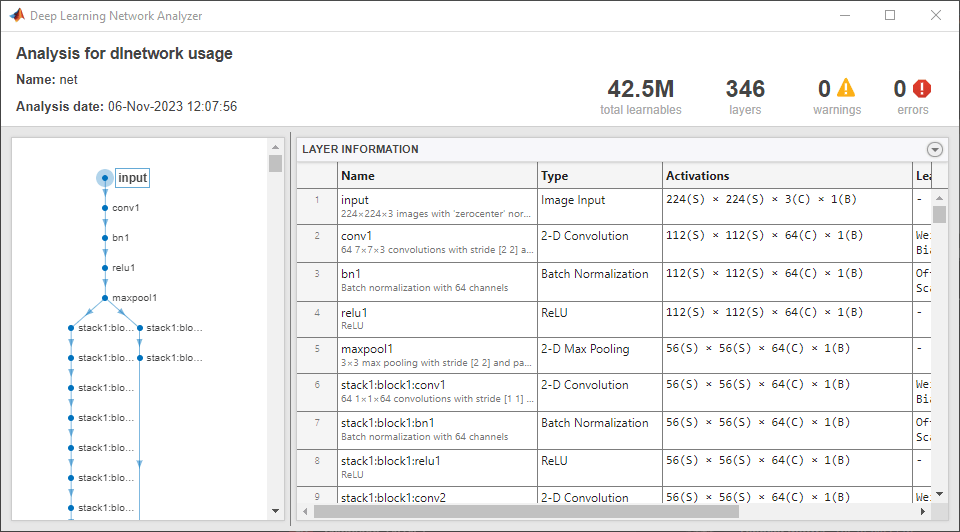
Create a ResNet-101 network using a custom stack depth.
imageSize = [224 224 3]; numClasses = 10; stackDepth = [3 4 23 3]; numFilters = [64 128 256 512]; net = resnetNetwork(imageSize,numClasses, ... StackDepth=stackDepth, ... NumFilters=numFilters)
net =
dlnetwork with properties:
Layers: [346×1 nnet.cnn.layer.Layer]
Connections: [378×2 table]
Learnables: [418×3 table]
State: [208×3 table]
InputNames: {'input'}
OutputNames: {'softmax'}
Initialized: 1
View summary with summary.
Analyze the network.
analyzeNetwork(net)
Input Arguments
Network image input size, specified as one of these values:
Vector of positive integers of the form
[h w]— Input has a height and width ofhandw, respectively.Vector of positive integers of the form
[h w c]— Input has a height, width, and number of channels ofh,w, andc, respectively. For RGB images,cis3, and for grayscale images,cis1.
The values of inputSize depend on the
InitialPoolingLayer argument:
If
InitialPoolingLayeris"max"or"average", then the spatial dimension sizes must be greater than or equal tok*2^(D+1), wherekis the value ofInitialStridein the first convolutional layer in the corresponding direction, andDis the number of downsampling blocks.If
InitialPoolingLayeris"none", then the spatial dimension sizes must be greater than or equal tok*2^D, wherekis the value ofInitialStridein the first convolutional layer in the corresponding direction.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Number of classes for classification tasks, specified as a positive integer.
The function returns a neural network for classification tasks with the specified number of classes by setting the output size of the last fully connected layer to numClasses.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: net =
resnetNetwork(inputSize,numClasses,BottleneckType="none") returns a 2-D residual
neural network without bottleneck components.
Initial Layers
Filter size in the first convolutional layer, specified as one of these values:
Positive integer — First convolutional layer has filters with a height and width of the specified value.
Vector of positive integers of the form
[h w]— First convolutional layer has filters with a height and width ofhandw, respectively.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Number of filters in the first convolutional layer, specified as a positive integer. The number of initial filters determines the number of channels (feature maps) in the output of the first convolutional layer in the residual network.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Stride in the first convolutional layer, specified as one of these values:
Positive integer — First convolutional layer has a vertical and horizontal stride of the specified value.
Vector of positive integers of the form
[h w]— First convolutional layer has a vertical and horizontal stride ofhandw, respectively.
The stride defines the step size for traversing the input vertically and horizontally.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
First pooling layer before the initial residual block, specified as one of these values:
"max"— Use a max pooling layer before the initial residual block. For more information, seemaxPooling2dLayer."average"— Use an average pooling layer before the initial residual block. For more information, seeaveragePooling2dLayer."none"— Do not use a pooling layer before the initial residual block.
Network Architecture
Residual block type, specified as one of these values:
The ResidualBlockType argument specifies the location of the batch
normalization layer in the standard and downsampling residual blocks. For more
information, see Residual Network.
Block bottleneck type, specified as one of these values:
"downsample-first-conv"— Use bottleneck residual blocks that perform downsampling, using a stride of 2, in the first convolutional layer of the downsampling residual blocks. A bottleneck residual block consists of three layers: a convolutional layer with filters of size 1 for downsampling the channel dimension, a convolutional layer with filters of size 3, and a convolutional layer with filters of size 1 for upsampling the channel dimension.The number of filters in the final convolutional layer is four times that in the first two convolutional layers.
"none"— Do not use bottleneck residual blocks. The residual blocks consist of two convolutional layers with filters of size 3.
A bottleneck block reduces the number of channels by a factor of four by performing a convolution with filters of size 1 before performing convolution with filters of size 3. Networks with and without bottleneck blocks have a similar level of computational complexity, but the total number of features propagating in the residual connections is four times larger when you use bottleneck units. Therefore, using a bottleneck increases the efficiency of the network [1].
For more information on the layers in each residual block, see Residual Network.
Number of residual blocks in each stack, specified as a vector of positive integers.
For example, if the stack depth is [3 4 6 3], the network has four stacks,
with three blocks, four blocks, six blocks, and three blocks.
Specify the number of filters in the convolutional layers of each stack using the NumFilters argument. StackDepth must have the same number of elements as NumFilters.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Number of filters in the convolutional layers of each stack, specified as a vector of positive integers.
If
BottleneckTypeis"downsample-first-conv", then the number of filters in each of the first two convolutional layers in each block of each stack isNumFilters. The final convolutional layer has four times the number of filters in each of the first two convolutional layers.For example, if
NumFiltersis[4 5]andBottleneckTypeis"downsample-first-conv", then in the first stack, the first two convolutional layers in each block have 4 filters and the final convolutional layer in each block has 16 filters. In the second stack, the first two convolutional layers in each block have 5 filters and the final convolutional layer has 20 filters.If
BottleneckTypeis"none", then the number of filters in each convolutional layer in each stack isNumFilters.
NumFilters must have the same number of elements as
StackDepth.
The NumFilters value determines the layers on the residual connection in
the initial residual block. The residual connection has a convolutional layer when you
meet one of these conditions:
BottleneckTypeis"downsample-first-conv", andInitialNumFiltersis not equal to four times the first element ofNumFilters.BottleneckTypeis"none", andInitialNumFiltersis not equal to the first element ofNumFilters.
For more information about the layers in each residual block, see Residual Network.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Data normalization to apply every time data forward-propagates through the input layer, specified as one of these options:
"zerocenter"— Subtract the mean of the training data."zscore"— Subtract the mean and then divide by the standard deviation of the training data.
The trainnet
function automatically calculates the mean and standard deviation of the training
data.
Flag to initialize learnable parameters, specified as a logical 1
(true) or 0 (false).
Output Arguments
Residual neural network, returned as a dlnetwork object.
More About
Residual networks (ResNets) are a type of deep network that consists of building blocks that have residual connections (also known as skip or shortcut connections). These connections allow the input to skip the convolutional units of the main branch, thus providing a simpler path through the network. By allowing the parameter gradients to flow more easily from the final layers to the earlier layers of the network, residual connections mitigate the problem of vanishing gradients during early training.
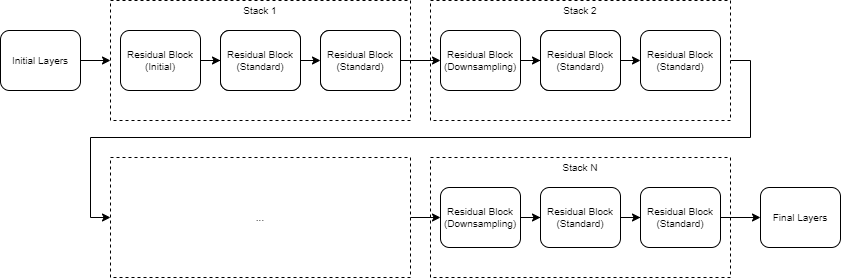
The structure of a residual network is flexible. The key component is the inclusion of the residual connections within residual blocks. A group of residual blocks is called a stack. A ResNet architecture consists of initial layers, followed by stacks containing residual blocks, and then the final layers. A network has three types of residual blocks:
Initial residual block — This block occurs at the start of the first stack. The layers in the residual connection of the initial residual block determine if the block preserves the activation sizes or performs downsampling.
Standard residual block — This block occurs multiple times in each stack, after the first downsampling residual block. The standard residual block preserves the activation sizes.
Downsampling residual block — This block occurs once, at the start of each stack. The first convolutional unit in the downsampling block downsamples the spatial dimensions by a factor of two.
A typical stack has a downsampling residual block, followed by
m standard residual blocks, where m is a positive
integer. The first stack is the only stack that begins with an initial residual block.
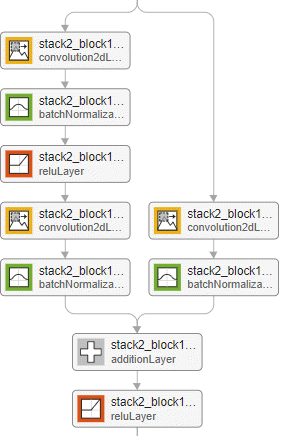
The initial, standard, and downsampling residual blocks can be bottleneck or nonbottleneck blocks.
A bottleneck block reduces the number of channels by a factor of four by performing a convolution with filters of size 1 before performing convolution with filters of size 3. Networks with and without bottleneck blocks have a similar level of computational complexity, but the total number of features propagating in the residual connections is four times larger when you use bottleneck units. Therefore, using a bottleneck increases the efficiency of the network [1].
The options you set determine the layers inside each block.
Block Layers
| Name | Initial Layers | Initial Residual Block | Standard Residual Block
(BottleneckType="downsample-first-conv") | Standard Residual Block
(BottleneckType="none") | Downsampling Residual Block | Final Layers |
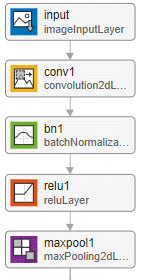
| Description | A residual network starts with these layers, in order:
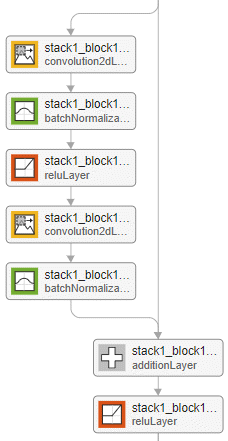
| The main branch of the initial residual block has the same layers as a standard residual block. The
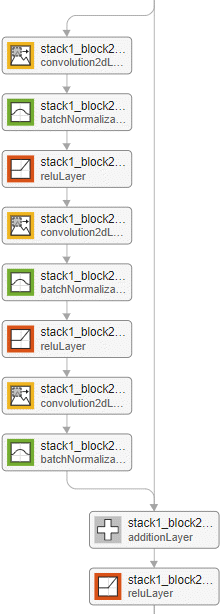
If | The standard residual block with bottleneck units has these layers, in order:
The standard block has a residual connection from the output of the previous block to the addition layer. Set the position of the addition layer using the
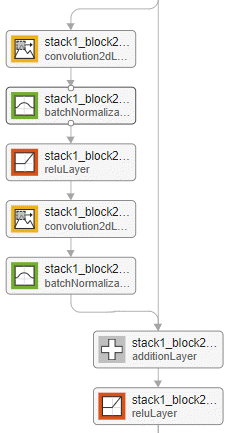
| The standard residual block without bottleneck units has these layers, in order:
The standard block has a residual connection from the output of the previous block to the addition layer. Set
the position of the addition layer using the
| The downsampling residual block is the same as the standard
block (either with or without the bottleneck) but with a stride of
size The
layers on the residual connection depend on the value of
The downsampling block halves the height and width of the input, and increases the number of channels. | A residual network ends with these layers, in order:
|
| Example Visualization |
| Example of an initial residual block for a network without a bottleneck and with the batch normalization layer before the addition layer.
| Example of the standard residual block for a network with a bottleneck and with the batch normalization layer before the addition layer.
| Example of the standard residual block for a network without a bottleneck and with the batch normalization layer before the addition layer.
| Example of a downsampling residual block for a network without a bottleneck and with the batch normalization layer before the addition layer.
|
|
The convolution and fully connected layer weights are initialized using the He weight initialization method [3].
Tips
When working with small images, set the
InitialPoolingLayeroption to"none"to remove the initial pooling layer and reduce the amount of downsampling.Residual networks are usually named ResNet-X, where X is the depth of the network. The depth of a network is defined as the largest number of sequential convolutional or fully connected layers on a path from the network input to the network output. You can use this formula to compute the depth of your network:
where si is the depth of stack i.
References
[1] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. “Deep Residual Learning for Image Recognition.” Preprint, submitted December 10, 2015. https://arxiv.org/abs/1512.03385.
[2] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. “Identity Mappings in Deep Residual Networks.” Preprint, submitted July 25, 2016. https://arxiv.org/abs/1603.05027.
[3] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification." In Proceedings of the 2015 IEEE International Conference on Computer Vision, 1026–34. Washington, DC: IEEE Computer Vision Society, 2015.
Version History
Introduced in R2024a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)