ワイブル分布モデルの当てはめ

ワイブル分布モデルについて

ワイブル分布は、信頼性や寿命 (故障率) のデータ解析に広く使用されます。ツールボックスでは、2 パラメーターのワイブル分布が用意されています

$y = a b x^{b - 1} e^{- a x^{b}}$

ここで、a はスケールパラメーターで、b は形状パラメーターです。

これ以外にも次のようなワイブル分布がありますが、これらの分布を使用するにはカスタム式を作成しなければならないことに注意してください。

x を x – c に置き換えた 3 パラメーターのワイブル分布。ここで c は位置パラメーター。
1 パラメーターのワイブル分布。形状パラメーターが固定されていて、スケールパラメーターのみが近似の対象。

Curve Fitting Toolbox™ では、ワイブル確率分布を使用してデータのサンプルを近似しません。その代わりに、応答データおよび予測子データを曲線で近似し、その曲線がワイブル分布と同じ形状をもつようにします。

ワイブルモデルによる対話的な近似

MATLAB^® コマンドラインで curveFitter と入力して曲線フィッターアプリを開きます。または、[アプリ] タブの [数学、統計および最適化] グループで [曲線フィッター] をクリックします。
曲線フィッターアプリで、曲線データを選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] および [Y データ] を選択するか、インデックスに対する [Y データ] のみを選択します。
[近似タイプ] セクションの矢印をクリックしてギャラリーを開き、[回帰モデル] グループの [ワイブル] をクリックします。

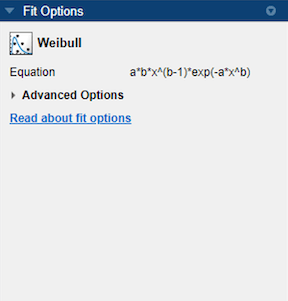
Fit Options pane for Weibull fit

[近似オプション] ペインで構成する近似設定はありません。

必要に応じて、[詳細オプション] セクションで係数の開始値と制約範囲を指定するか、アルゴリズム設定を変更します。区間 [0 1] で定義される、[ワイブル] 近似のランダムな開始点がアプリによって計算されます。開始点をオーバーライドして、[近似オプション] ペインで独自の値を指定することができます。

設定の詳細については、係数の制約: 範囲と最適化された開始点の指定を参照してください。

コマンドラインでのワイブル近似の選択

モデルタイプ weibull を指定します。

たとえば、ある化合物の血中濃度を時間に対して測定したサンプルデータを読み込み、開始点を指定したワイブルモデルで近似およびプロットするには次のようにします。

time = [ 0.1;   0.1;   0.3;   0.3;   1.3;   1.7;   2.1;...
   2.6;   3.9;   3.9; ...
         5.1;   5.6;   6.2;   6.4;   7.7;   8.1;   8.2;...
   8.9;   9.0;   9.5; ...
         9.6;  10.2;  10.3;  10.8;  11.2;  11.2;  11.2;...
  11.7;  12.1;  12.3; ...
        12.3;  13.1;  13.2;  13.4;  13.7;  14.0;  14.3;...
  15.4;  16.1;  16.1; ...
        16.4;  16.4;  16.7;  16.7;  17.5;  17.6;  18.1;...
  18.5;  19.3;  19.7;];
conc = [0.01;  0.08;  0.13;  0.16;  0.55;  0.90;  1.11;...
  1.62;  1.79;  1.59; ...
        1.83;  1.68;  2.09;  2.17;  2.66;  2.08;  2.26;...
  1.65;  1.70;  2.39; ...
        2.08;  2.02;  1.65;  1.96;  1.91;  1.30;  1.62;...
  1.57;  1.32;  1.56; ...
        1.36;  1.05;  1.29;  1.32;  1.20;  1.10;  0.88;...
  0.63;  0.69;  0.69; ...
        0.49;  0.53;  0.42;  0.48;  0.41;  0.27;  0.36;...
  0.33;  0.17;  0.20;];

f=fit(time, conc/25, 'Weibull', ...
'StartPoint', [0.01, 2] )
plot(f,time,conc/25, 'o');

係数の開始値や制約範囲などの近似オプションをデータに合わせて変更したり、アルゴリズム設定を変更したりする場合は、fitoptions のリファレンスページにある NonlinearLeastSquares の追加プロパティの表を参照してください。

2 パラメーターのワイブルモデルにおける適切な開始点の値とスケーリングである conc/25 は、次のカスタム式を使用して 3 パラメーターのワイブルモデルを当てはめて計算しました。

f=fit(time, conc, ' c*a*b*x^(b-1)*exp(-a*x^b)', 'StartPoint', [0.01, 2, 5] )

f = 
     General model:
     f(x) = c*a*b*x^(b-1)*exp(-a*x^b)
     Coefficients (with 95% confidence bounds):
       a =    0.009854  (0.007465, 0.01224)
       b =       2.003  (1.895, 2.11)
       c =       25.65  (24.42, 26.89)

このワイブルモデルは 3 つのパラメーターで定義されます。最初のパラメーターは曲線を横軸に沿ってスケーリングします。2 番目のパラメーターは曲線の形状を規定します。3 番目のパラメーターは曲線を縦軸に沿ってスケーリングします。この曲線の形状が、ワイブル確率密度関数の形状とほぼ同じでありながら、パラメーター c を含んでいるために密度ではないことに注意してください。このパラメーター c は、データに合わせて曲線の高さを調整するために必要です。

参考