Lowess 平滑化

Lowess 平滑化について

Lowess モデルを使用して、滑らかな曲面をデータに当てはめます。"lowess" および "loess" という名前は "locally weighted scatter plot smooth (局所的に重み付けされた散布図平滑化)" から来ており、どちらの手法も局所的に重み付けされた線形回帰を使用してデータを平滑化します。ツールボックスでは所定の範囲に含まれるデータ点の回帰重み関数が定義されるため、このプロセスは "重み付け" を伴います。回帰重み関数に加え、[ロバスト] オプションは、外れ値に対する耐性をこのプロセスにもたせることができる重み関数です。

これら 2 つのタイプの平滑化近似の詳細については、局所回帰平滑化を参照してください。

Lowess 近似の対話的な選択

MATLAB^® コマンドラインで curveFitter と入力して曲線フィッターアプリを開きます。または、[アプリ] タブの [数学、統計および最適化] グループで [曲線フィッター] をクリックします。

[曲線フィッター] タブの [近似タイプ] セクションで [局所回帰平滑化 (Lowess)] 近似を選択します。アプリは、局所的に重み付けされた線形回帰を使用してデータを平滑化します。

[近似オプション] ペインで、さまざまなオプションを試すことができます。

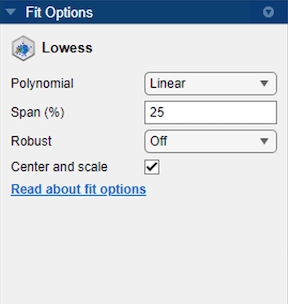
Fit Options pane for lowess fit

回帰 [多項式] モデルは、Linear または Quadratic に設定できます。
[範囲] を使用して、データセットの合計データ点数の割合として範囲を設定できます。この範囲内で定義される隣接データ点を使用してそれぞれの平滑化値が決定されます。この平滑化プロセスは "局所" と呼ばれます。
ヒント
範囲を増やすと曲面が滑らかになります。範囲を減らすと曲面がより密接にデータに追従します。
[ロバスト] 線形最小二乗近似法は、Off、LAR、または Bisquare に設定できます。局所回帰は [ロバスト] オプションを使用します。[ロバスト] 重み関数を使用すると、外れ値に対する耐性を平滑化にもたせることができます。詳細については、関数 fitoptions の名前と値の引数 Robust を参照してください。

ヒント

データ変数間のスケールが大きく異なる場合は、[データのセンタリングとスケーリング] チェックボックスがオンの場合とオフの場合とで近似の違いを確認してください。変数の正規化は lowess 近似の結果に大きな影響を与える場合があります。

lowess 近似を対話的に作成する方法の例については、フランケデータの曲面近似を参照してください。

関数 `fit` を使用した Lowess モデルによる近似

ライブスクリプトを開く

この例では、関数 fit を使用して Lowess モデルによりデータを近似する方法を示します。

関数 fit の呼び出し時に 'lowess' を指定することで、データを読み込んで、Lowess モデルにより近似します。

load franke
f = fit([x y],z,'lowess')

     Locally weighted smoothing linear regression:
       f(x,y) = lowess (linear) smoothing regression computed from p
     Coefficients:
       p = coefficient structure

plot(f,[x y],z)

Figure contains an axes object. The axes object contains 2 objects of type surface, line. One or more of the lines displays its values using only markers