対数モデルの当てはめ

対数モデルについて

対数モデルは、最初に急峻に増加する期間があり、その後はそれよりも遅いレートで増加していきます。対数モデルは、人口増加や信号処理の調査など、さまざまな用途に使用されます。Curve Fitting Toolbox™ は、次の表に記載された対数モデルをサポートしています。

対数モデル	基底	方程式
自然対数	e	`Y = a*log(x)+b`
常用対数	`10`	`Y = a*log10(x)+b`
2 進対数	`2`	`Y = a*log2(x)+b`

上記の方程式で、a はスケーリングパラメーター、b は x = 1 のときの Y の値です。基底の変換公式 $\log_{j} (x) = \frac{l o g_{i} (x)}{l o g_{i} (j)}$ を使用して、異なる対数モデルの間で変換できます。ここで、j は変換先のモデルの基底、i は変換元のモデルの基底です。データへの当てはめに使用する対数モデルは、解を求める問題のタイプによって異なります。

曲線フィッターを使用した対数モデルの当てはめ

ライブスクリプトを開く

linspace、log2、およびrandn関数を使用してノイズを含むデータをいくつか生成します。

rng(0,"twister") %  For reproducibility
x = linspace(0.01,3,100)';
y = log2(x) + 0.2*randn(100,1);

コマンドラインから曲線フィッターアプリを開きます。

curveFitter

または、[アプリ] タブの [数学、統計および最適化] グループで [曲線フィッター] をクリックします。

曲線フィッターアプリで、近似のデータ変数を選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] の値として x、[Y データ] の値として y を選択します。

変数を選択すると、アプリによってデータ点がプロットされます。既定で、アプリは多項式をデータに当てはめます。対数モデルを当てはめるには、[曲線フィッター] タブの [近似タイプ] セクションで Logarithmic をクリックします。

アプリにより、自然対数モデルが当てはめられます。

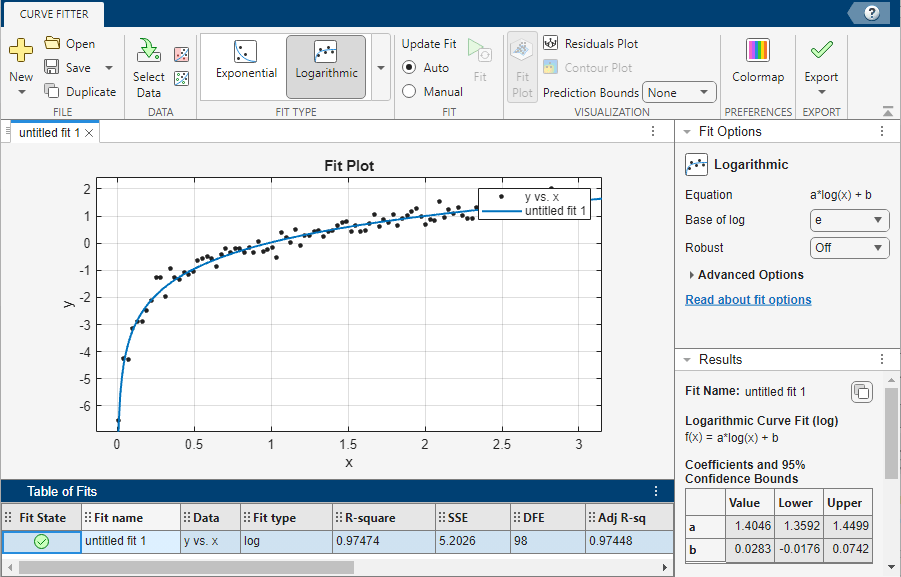
当てはめられた自然対数モデルは、x の値が小さいうちは比較的急速に増加します。[結果] パネルに、自然対数モデルの式、および 95% の区間をもつ近似係数が表示されます。[近似テーブル] は、当てはめられたモデルの誤差二乗和 (SSE) が約 5.2、決定係数の値が約 0.97 であることを示しています。

この自然対数モデルを 2 進対数モデルと比較するには、[近似オプション] パネルの [対数の基底] に 2 を選択します。アプリにより、2 進対数モデルがデータに当てはめられます。

[近似テーブル] は、当てはめられた自然対数モデルと当てはめられた 2 進対数モデルで SSE と決定係数の値が同じであることを示しています。また、プロットも、当てはめられたモデルが同じであることを示しています。これらのモデルで異なるのは、対数モデルの基底、および係数 "a" の値と信頼限界だけです。方程式 $l o g_{2} (x) = \frac{l o g (x)}{l o g (2)}$ および $l o g (x) = \frac{l o g_{2} (x)}{l o g_{2} (e)}$ を使用すると、自然対数モデルと 2 進対数モデルを相互に手動で変換できます。

既定では、アプリは線形最小二乗近似を使用して近似係数を計算します。[近似オプション] パネルの [ロバスト] メニューからロバスト近似法を選択できます。たとえば、二重平方重み法を使用するには Bisquare を選択します。

[近似テーブル] は、2 進対数モデルでは線形最小二乗近似を使用するよりも二重平方重み近似を使用した方が SSE がわずかに小さく、決定係数の値がわずかに大きいことを示しています。

コマンドラインからの対数モデルの当てはめ

ライブスクリプトを開く

linspace、log10、およびrandn関数を使用してノイズを含むデータをいくつか生成します。

rng(0,"twister") %  For reproducibility
x = linspace(0.01,3,100)';
y = log10(x) + 0.1*randn(100,1);

常用対数モデルをデータに当てはめます。

f = fit(x,y,"log10")

f = 
     Linear model Log10:
     f(x) = a*log10(x) + b
     Coefficients (with 95% confidence bounds):
       a =      0.9561  (0.9039, 1.008)
       b =     0.01415  (-0.008812, 0.03712)

f は、データに常用対数モデルを当てはめた結果を含むcfitオブジェクトです。出力には、常用対数モデルの式、および 95% 信頼限界の近似係数が表示されます。

f とデータをプロットします。

plot(f,x,y)

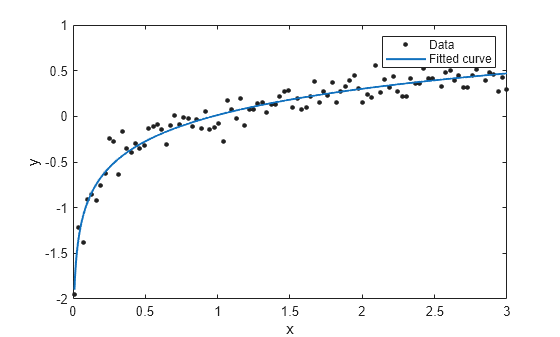
Figure contains an axes object. The axes object with xlabel x, ylabel y contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fitted curve.

プロットは、f が大部分のデータに追従していることを示しています。

参考