2 ループ自動操縦の調整
この例では、Simulink® Control Design™ を使用して機体のピッチ レートと垂直加速度を制御する 2 ループ自動操縦を調整する方法を説明します。
機体自動操縦のモデル
機体のダイナミクスと自動操縦は Simulink でモデル化されます。
open_system('rct_airframe1')
自動操縦は 2 つのカスケード式ループで構成されています。操縦かんコマンド azref への応答で、内側のループはピッチ レート q を制御し、外側のループは垂直加速度 az を制御します。このアーキテクチャでは、調整可能な要素に PI コントローラー ゲイン ("az Control" ブロック) とピッチレート ゲイン ("q Gain" ブロック) が含まれます。自動操縦は、最小限のオーバーシュートでステップ コマンド azref に約 1 秒で応答するように調整されなければなりません。この例では、0 の入射と 984 m/s の速度に対応する 1 つの飛行条件に対して自動操縦ゲインを調整します。
機体のダイナミクスを解析するには、
と 
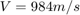で機体を平衡化します。平衡化条件は、0 の法線加速度とピッチのモーメント (
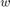および 
の定常状態) に相当します。findop を使用して対応する閉ループ操作条件を計算します。"delta trim" 入力端子を追加して、力とモーメントの望ましい平衡状態が生成されるよう、findop でフィンの偏向角を調整できるようにしたことに注意してください。
opspec = operspec('rct_airframe1'); % Specify trim condition % Xe,Ze: known, not steady opspec.States(1).Known = [1;1]; opspec.States(1).SteadyState = [0;0]; % u,w: known, w steady opspec.States(3).Known = [1 1]; opspec.States(3).SteadyState = [0 1]; % theta: known, not steady opspec.States(2).Known = 1; opspec.States(2).SteadyState = 0; % q: unknown, steady opspec.States(4).Known = 0; opspec.States(4).SteadyState = 1; % integrator states unknown, not steady opspec.States(5).SteadyState = 0; opspec.States(6).SteadyState = 0; op = findop('rct_airframe1',opspec);
Operating point search report:
---------------------------------
opreport =
Operating point search report for the Model rct_airframe1.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
___________ ___________ ___________ ___________ ___________ ___________
(1.) rct_airframe1/Airframe Model/Aerodynamics & Equations of Motion/ Equations of Motion (Body Axes)/Position
0 0 0 -Inf 984 Inf
-3047.9999 -3047.9999 -3047.9999 -Inf 0 Inf
(2.) rct_airframe1/Airframe Model/Aerodynamics & Equations of Motion/ Equations of Motion (Body Axes)/Theta
0 0 0 -Inf -0.0097235 Inf
(3.) rct_airframe1/Airframe Model/Aerodynamics & Equations of Motion/ Equations of Motion (Body Axes)/U,w
984 984 984 -Inf 22.6897 Inf
0 0 0 0 -1.4367e-11 0
(4.) rct_airframe1/Airframe Model/Aerodynamics & Equations of Motion/ Equations of Motion (Body Axes)/q
-Inf -0.0097235 Inf 0 1.1477e-16 0
(5.) rct_airframe1/Integrator
-Inf 0.00070807 Inf -Inf -0.0097235 Inf
(6.) rct_airframe1/az Control/Integrator/Continuous/Integrator
-Inf 0 Inf -Inf 0.00024207 Inf
Inputs:
----------
Min u Max
__________ __________ __________
(1.) rct_airframe1/delta trim
-Inf 0.00070807 Inf
Outputs: None
----------
計算された平衡化条件 op に対し "Airframe Model" ブロックを線形化し、フィンの偏向角 delta から az および q へのゲインをプロットします。
G = linearize('rct_airframe1','rct_airframe1/Airframe Model',op); G.InputName = 'delta'; G.OutputName = {'az','q'}; bodemag(G), grid
機体モデルには不安定な極があることに注意してください。
pole(G)
ans =
-0.0320
-0.0255
0.1253
-29.4685
LOOPTUNE を使用した周波数領域の調整
関数 looptune を使用すると、積分動作、適切な安定余裕、目的の帯域幅などの基本要件に従ってマルチループ制御システムを自動的に調整できます。looptune を自動操縦モデルに適用するには、slTuner インターフェイスのインスタンスを作成し、Simulink ブロック "az Control" および "q Gain" を調整可能として指定します。また、平衡化条件 op を指定して機体のダイナミクスを正しく線形化します。
ST0 = slTuner('rct_airframe1',{'az Control','q Gain'},op);
基準信号、制御信号および測定信号を解析と調整の対象のポイントとしてマークします。
addPoint(ST0,{'az ref','delta fin','az','q'});
最後に、1 秒の応答時間要件を満たすように制御システム パラメーターを調整します。周波数領域では、これはプラント入力 "delta fin" における開ループ応答でのゲイン交差周波数 wc = 5 rad/s とほぼ一致します。
wc = 5; Controls = 'delta fin'; Measurements = {'az','q'}; [ST,gam,Info] = looptune(ST0,Controls,Measurements,wc);
Final: Peak gain = 1.01, Iterations = 72
要件は正規化され、1 に近い最終的な値はすべての要件が満たされていることを意味します。これを確認するには、設計をグラフで検証します。
figure('Position',[100,100,560,714])
loopview(ST,Info)
1 つ目のプロットでは開ループ応答に積分動作と目的のゲイン交差周波数があることが確認でき、2 つ目のプロットでは MIMO 安定余裕が満たされている (青い曲線が黄色の範囲を下回る状態) ことがわかります。次に、ステップ コマンド azref から垂直加速度 az への応答をチェックします。
T = getIOTransfer(ST,'az ref','az'); figure step(T,5)
ループ内に積分器が存在しても、加速度 az は azref を追従しません。これは、フィードバック ループが 2 つの変数 az および q を処理し、そのどちらが azref を追従するかを指定していないためです。
追従要件の追加
この問題を修正するには、az は 1 秒の応答時間でステップ コマンド azref に追従するという明示的な要件を追加します。また、ゲイン交差要件を間隔 [3,12] に緩和して、調整器が適切なゲイン交差周波数を検出できるようにします。
TrackReq = TuningGoal.Tracking('az ref','az',1); ST = looptune(ST0,Controls,Measurements,[3,12],TrackReq);
Final: Peak gain = 1.23, Iterations = 51
これで、azref から az へのステップ応答は適切になります。
Tr1 = getIOTransfer(ST,'az ref','az'); step(Tr1,5) grid
また、プラント入力に入る外乱からの応答を確認して外乱の抑制の特性をチェックします。
Td1 = getIOTransfer(ST,'delta fin','az'); bodemag(Td1) grid
step(Td1,5)
grid
title('Disturbance rejection')
showBlockValue を使用して、PI コントローラーと内側のループ ゲインの調整後の値を確認します。
showBlockValue(ST)
AnalysisPoints_ =
D =
u1 u2 u3 u4
y1 1 0 0 0
y2 0 1 0 0
y3 0 0 1 0
y4 0 0 0 1
Name: AnalysisPoints_
Static gain.
-----------------------------------
az_Control =
1
Kp + Ki * ---
s
with Kp = 0.00166, Ki = 0.0017
Name: az_Control
Continuous-time PI controller in parallel form.
-----------------------------------
q_Gain =
D =
u1
y1 1.985
Name: q_Gain
Static gain.
この設計で十分である場合は、writeBlockValue を使用して調整後の値を Simulink モデルに適用し、調整後のコントローラーを Simulink でシミュレートします。
writeBlockValue(ST)
SYSTUNE による MIMO の設計
通常、自動操縦にはカスケード式ループが使用されます。しかし、az と q の両方を使用してアクチュエータ コマンド delta fin を生成する単一の MIMO コントローラーは、2 ループ アーキテクチャとどのような違いがあるのでしょうか。systune または looptune を使用すると、新しい制御アーキテクチャを簡単に試すことができます。ここでは趣向を変えて、systune を使用して次の MIMO アーキテクチャを調整します。
open_system('rct_airframe2')
前と同様に、 と 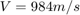の平衡化条件を計算します。
opspec = operspec('rct_airframe2'); % Specify trim condition % Xe,Ze: known, not steady opspec.States(1).Known = [1;1]; opspec.States(1).SteadyState = [0;0]; % u,w: known, w steady opspec.States(3).Known = [1 1]; opspec.States(3).SteadyState = [0 1]; % theta: known, not steady opspec.States(2).Known = 1; opspec.States(2).SteadyState = 0; % q: unknown, steady opspec.States(4).Known = 0; opspec.States(4).SteadyState = 1; % controller states unknown, not steady opspec.States(5).SteadyState = [0;0]; op = findop('rct_airframe2',opspec);
Operating point search report:
---------------------------------
opreport =
Operating point search report for the Model rct_airframe2.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
___________ ___________ ___________ ___________ ___________ ___________
(1.) rct_airframe2/Airframe Model/Aerodynamics & Equations of Motion/ Equations of Motion (Body Axes)/Position
0 0 0 -Inf 984 Inf
-3047.9999 -3047.9999 -3047.9999 -Inf 0 Inf
(2.) rct_airframe2/Airframe Model/Aerodynamics & Equations of Motion/ Equations of Motion (Body Axes)/Theta
0 0 0 -Inf -0.0097235 Inf
(3.) rct_airframe2/Airframe Model/Aerodynamics & Equations of Motion/ Equations of Motion (Body Axes)/U,w
984 984 984 -Inf 22.6897 Inf
0 0 0 0 2.4588e-11 0
(4.) rct_airframe2/Airframe Model/Aerodynamics & Equations of Motion/ Equations of Motion (Body Axes)/q
-Inf -0.0097235 Inf 0 -4.0169e-16 0
(5.) rct_airframe2/MIMO Controller
-Inf 0.00065361 Inf -Inf -0.0089973 Inf
-Inf 2.6167e-19 Inf -Inf 0.030259 Inf
Inputs:
----------
Min u Max
__________ __________ __________
(1.) rct_airframe2/delta trim
-Inf 0.00043574 Inf
Outputs: None
----------
looptune と同様に、slTuner インターフェイスを使用して Simulink モデルを調整用に構成します。対象の信号が Simulink モデルで既に線形解析ポイントとしてマークされていることに注意してください。
ST0 = slTuner('rct_airframe2','MIMO Controller',op);
e から delta fin へのゼロの直達を使用する 2 次 MIMO コントローラーを試します。これを行うには、目的のコントローラー パラメーター化を作成し、setBlockParam を使用して "MIMO Controller" ブロックに関連付けます。
C0 = tunableSS('C',2,1,2); % Second-order controller C0.D.Value(1) = 0; % Fix D(1) to zero C0.D.Free(1) = false; setBlockParam(ST0,'MIMO Controller',C0)
次に、調整要件を作成します。ここでは、以下の 4 つの要件を使用します。
追従:
azはazrefコマンドに約 1 秒で応答する帯域幅とロールオフ:
delta finのループ ゲインは、-20 dB/decade の傾きで 25 rad/s の後にロールオフする安定余裕:
delta finの余裕は 7 dB および 45 度を超える外乱の抑制: 入力外乱の減衰係数は 1 rad/s で 40 dB となり、0.001 rad/s で 100 dB まで増える
% Tracking Req1 = TuningGoal.Tracking('az ref','az',1); % Bandwidth and roll-off Req2 = TuningGoal.MaxLoopGain('delta fin',tf(25,[1 0])); % Margins Req3 = TuningGoal.Margins('delta fin',7,45); % Disturbance rejection % Use an FRD model to sketch the desired attenuation profile with a few points Freqs = [0 0.001 1]; MinAtt = [100 100 40]; % in dB Req4 = TuningGoal.Rejection('delta fin',frd(db2mag(MinAtt),Freqs)); Req4.Focus = [0 1];
これで、systune を使用して、これらの要件に従ってコントローラー パラメーターを調整できます。
AllReqs = [Req1,Req2,Req3 Req4];
Opt = systuneOptions('RandomStart',3);
rng(0)
[ST,fSoft] = systune(ST0,AllReqs,Opt);
Final: Soft = 1.42, Hard = -Inf, Iterations = 47 Final: Soft = 1.42, Hard = -Inf, Iterations = 62 Final: Soft = 1.14, Hard = -Inf, Iterations = 93 Final: Soft = 1.14, Hard = -Inf, Iterations = 127
最適な設計では全体的な目的値が 1 に近くなり、4 つのすべての要件がほぼ満たされることを示します。viewGoal を使用して、最適な設計の各要件を検査します。
figure('Position',[100,100,987,474])
viewGoal(AllReqs,ST)
閉ループ応答を計算し、2 ループ設計と比較します。
T = getIOTransfer(ST,{'az ref','delta fin'},'az');
figure
step(Tr1,'b',T(1),'r',5)
title('Tracking')
legend('Cascade','2 dof')
ans =
Legend (Cascade, 2 dof) with properties:
String: {'Cascade' '2 dof'}
Location: 'northeast'
Orientation: 'vertical'
FontSize: 9
Position: [0.7030 0.7695 0.1830 0.0789]
Units: 'normalized'
Use GET to show all properties
step(Td1,'b',T(2),'r',5) title('Disturbance rejection') legend('Cascade','2 dof')
ans =
Legend (Cascade, 2 dof) with properties:
String: {'Cascade' '2 dof'}
Location: 'northeast'
Orientation: 'vertical'
FontSize: 9
Position: [0.7030 0.7695 0.1830 0.0789]
Units: 'normalized'
Use GET to show all properties
追従性能は同様ですが、外乱の抑制プロパティについては 2 番目の設計の方が優れています。
参考
looptune (slTuner) (Simulink Control Design) | slTuner (Simulink Control Design)
関連するトピック
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)