蒸留塔の分離コントローラー

この例では、looptune を使用して蒸留塔の 2 つの主要なフィードバック ループを分離する方法を説明します。

蒸留塔モデル

この例では、次に示す蒸留塔の単純なモデルを使用しています。

図 1: 蒸留塔

いわゆる LV 構成では、制御変数は、化学薬品 D (上) と B (下) の濃度 yD および yB で、操作変数は還流 L と煮沸 V です。この過程は、L と V の一部の組み合わせに対する定常状態のゲインにおいて強い干渉と大きな変動を示します。詳細については、Skogestad および Postlethwaite 著『Multivariable Feedback Control』を参照してください。

プラントは、入力 L,V と出力 yD,yB をもつ 1 次伝達関数としてモデル化されます。

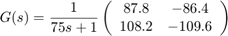
時間の単位は分です (すべてのプロットは秒ではなく分単位で表されます)。

s = tf('s');
G = [87.8 -86.4 ; 108.2 -109.6]/(75*s+1);
G.InputName = {'L','V'};
G.OutputName = {'yD','yB'};

制御アーキテクチャ

制御目的は次のとおりです。

• 上の設定値 Dsp の変更が下の濃度 B にほとんど影響しないこと、およびその逆も同様であることの確実化による、上の濃度と下の濃度の個別制御

• 15% 未満のオーバーシュートでの約 4 分間の応答時間

• 有効な還流 L と煮沸 V に影響する入力外乱の迅速な抑制

これらの目的を実現するためには、次に示す制御アーキテクチャを使用します。このアーキテクチャは、静的な分離行列 DM が、還流 L と煮沸 V の 2 つの PI コントローラーと直列につながれて構成されています。

open_system('rct_distillation')

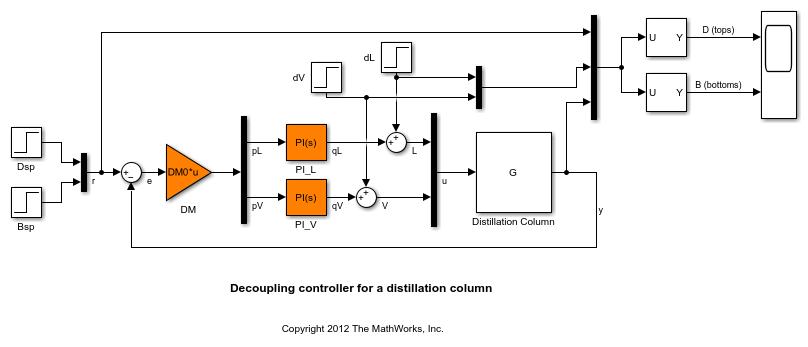
LOOPTUNE による Simulink でのコントローラーの調整

looptune コマンドを使うと、MIMO フィードバック ループをすばやく調整できます。制御システムが Simulink でモデル化されている場合、調整ブロック、制御信号と測定信号、および目的の帯域幅を指定するだけで、looptune により問題が自動的に設定されて、コントローラー パラメーターが調整されます。looptune は積分動作、ロールオフ、および適切な MIMO 安定余裕を提供する開ループ応答を成形します。

slTuner インターフェイスを使用して、閉ループ検証の対象となる調整ブロック、コントローラー I/O、および信号を指定します。

ST0 = slTuner('rct_distillation',{'PI_L','PI_V','DM'});

% Signals of interest
addPoint(ST0,{'r','dL','dV','L','V','y'})

開ループ応答のゲイン交差周波数を指定して制御帯域幅を設定します。4 分の応答時間の場合、交差周波数はおよそ 2/4 = 0.5 rad/min になります。

wc = 0.5;

TuningGoal オブジェクトを使用して、残りの制御目的を指定します。ステップ コマンドへの応答のオーバーシュートは 15% 未満でなければなりません。プラント入力におけるステップ外乱への応答は適切に減衰され、20 分未満で整定される必要があり、振幅は 4 を超えてはなりません。

OS = TuningGoal.Overshoot('r','y',15);

DR = TuningGoal.StepRejection({'dL','dV'},'y',4,20);

次に、looptune を使用して、コントローラー ブロック PI_L、PI_V、および DM を外乱の抑制要件に合わせて調整します。

Controls = {'L','V'};
Measurements = 'y';
[ST,gam,Info] = looptune(ST0,Controls,Measurements,wc,OS,DR);

Final: Peak gain = 0.996, Iterations = 58
Achieved target gain value TargetGain=1.

最終的な値は、すべての要件が満たされたことを示す 1 に近い値になります。loopview を使用して結果の設計をチェックします。応答は、影が付いた領域の外側になければなりません。

figure('Position',[0,0,1000,1200])
loopview(ST,Info)

getIOTransfer を使用して、上下の濃度に対する参照および外乱から閉ループ応答にアクセスし、プロットします。調整後の応答には、追従と外乱の抑制のバランスが取れていることが示されます。

figure
Ttrack = getIOTransfer(ST,'r','y');
step(Ttrack,40), grid, title('Setpoint tracking')

Treject = getIOTransfer(ST,{'dV','dL'},'y');
step(Treject,40), grid, title('Disturbance rejection')

周波数領域での開ループと閉ループの外乱の抑制の特性を比較すると、制御帯域幅内で明らかな改善が見られます。

clf, sigma(G,Treject), grid
title('Principal gains from input disturbances to outputs')
legend('Open-loop','Closed-loop')

調整後の変数への制約の追加

上記で取得したコントローラーの検証では、2 番目の PI コントローラーに負のゲインがあることが示されています。

getBlockValue(ST,'PI_V')

ans =
 
             1 
  Kp + Ki * ---
             s 

  with Kp = -4.12, Ki = -0.563
 
Name: PI_V
Continuous-time PI controller in parallel form.

これは、プラント の 2 番目の入力チャネルに負の符号があることが原因です。また、DM に 2 を乗算して PI ゲインを 2 で除算してもコントローラー全体は変更されないため、調整可能な要素は過剰にパラメーター化されています。これらの問題に対処するには、DM の (1,1) エントリを 1 に固定し、(2,2) エントリを -1 に固定します。

DM = getBlockParam(ST0,'DM');
DM.Gain.Value = diag([1 -1]);
DM.Gain.Free = [false true;true false];
setBlockParam(ST0,'DM',DM)

簡約された一連の調整可能なパラメーターでコントローラーを再調整します。

[ST,gam,Info] = looptune(ST0,Controls,Measurements,wc,OS,DR);

Final: Peak gain = 0.998, Iterations = 87
Achieved target gain value TargetGain=1.

ステップ応答は同じように見えますが、DM および PI ゲインの値は実装にさらに適したものになります。

figure('Position',[0,0,700,350])

subplot(121)
Ttrack = getIOTransfer(ST,'r','y');
step(Ttrack,40), grid, title('Setpoint tracking')

subplot(122)
Treject = getIOTransfer(ST,{'dV','dL'},'y');
step(Treject,40), grid, title('Disturbance rejection')

showTunable(ST)

Block 1: rct_distillation/PI_L =
 
             1 
  Kp + Ki * ---
             s 

  with Kp = 16.3, Ki = 2.15
 
Name: PI_L
Continuous-time PI controller in parallel form.

-----------------------------------

Block 2: rct_distillation/PI_V =
 
             1 
  Kp + Ki * ---
             s 

  with Kp = 12.8, Ki = 1.7
 
Name: PI_V
Continuous-time PI controller in parallel form.

-----------------------------------

Block 3: rct_distillation/DM =
 
  D = 
            u1       u2
   y1        1  -0.7729
   y2    1.251       -1
 
Name: DM
Static gain.

MATLAB での同等のワークフロー

制御システムの Simulink モデルがない場合は、LTI オブジェクトと制御設計ブロックを使用して次のブロック線図の MATLAB 表現を作成できます。

図 2: 制御システムのブロック線図

最初に、制御設計ブロックを使用して調整可能な要素をパラメーター化します。tunableGain オブジェクトを使用して DM をパラメーター化し、DM(1,1)=1 および DM(2,2)=-1 を固定します。これにより、調整可能なパラメーターとして非対角エントリをもつ 2 行 2 列の静的ゲインが作成されます。

DM = tunableGain('Decoupler',diag([1 -1]));
DM.Gain.Free = [false true;true false];

同様に、tunablePID オブジェクトを使用して 2 つの PI コントローラーをパラメーター化します。

PI_L = tunablePID('PI_L','pi');
PI_V = tunablePID('PI_V','pi');

次に、図 2 のコントローラー のモデル C0 を作成します。

C0 = blkdiag(PI_L,PI_V) * DM * [eye(2) -eye(2)];

% Note: I/O names should be consistent with those of G
C0.InputName = {'Dsp','Bsp','yD','yB'};
C0.OutputName = {'L','V'};

ここで、looptune を使用して、以前行ったようにコントローラー パラメーターを調整します。

% Crossover frequency
wc = 0.5;

% Overshoot and disturbance rejection requirements
OS = TuningGoal.Overshoot({'Dsp','Bsp'},{'yD','yB'},15);
DR = TuningGoal.StepRejection({'L','V'},{'yD','yB'},4,20);

% Tune controller gains
[~,C] = looptune(G,C0,wc,OS,DR);

Final: Peak gain = 0.998, Iterations = 71
Achieved target gain value TargetGain=1.

設計を検証するには、調整後の補償器 C でループを閉じて、設定点の追従と外乱の抑制のステップ応答をシミュレートします。

Tcl = connect(G,C,{'Dsp','Bsp','L','V'},{'yD','yB'});

figure('Position',[0,0,700,350])

subplot(121)
Ttrack = Tcl(:,[1 2]);
step(Ttrack,40), grid, title('Setpoint tracking')

subplot(122)
Treject = Tcl(:,[3 4]);
Treject.InputName = {'dL','dV'};
step(Treject,40), grid, title('Disturbance rejection')

結果は、Simulink で得られるものと同様の結果になります。

参考

looptune | looptune (slTuner) (Simulink Control Design)

関連するトピック

• デジタル モーション制御システムの調整