劣化するバッテリー システムの非線形の状態推定
この例では、Simulink® でアンセンテッド カルマン フィルターを使用して非線形システムの状態を推定する方法を説明します。また、イベントベースのカルマン フィルターを開発してシステム パラメーターを更新し、状態推定の精度を高める方法についても説明します。この例では Simscape™ および Stateflow® も必要です。
概要
次のような等価回路をもつバッテリー モデルについて考えます [1]。

モデルは電圧源 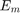 、直列抵抗
、直列抵抗  、そしてコンポーネント
、そしてコンポーネント  および
および  をもつ 1 つの RC ブロックで構成されています。バッテリーは充電と放電のサイクルを交互に繰り返します。この例では、測定された電流、電圧およびバッテリー温度の値を使用してバッテリー モデルの充電状態 (SOC) を推定します。バッテリーは非線形システムであると仮定し、アンセンテッド カルマン フィルターを使って SOC を推定します。バッテリーの容量は各放電サイクルごとに低下するため、SOC の推定値が不正確になります。イベントベースの線形カルマン フィルターを使用して、バッテリーが充電状態から放電状態に切り替わるときにバッテリー容量を推定します。次に、推定された容量を使用してバッテリーの健全性を示します。
をもつ 1 つの RC ブロックで構成されています。バッテリーは充電と放電のサイクルを交互に繰り返します。この例では、測定された電流、電圧およびバッテリー温度の値を使用してバッテリー モデルの充電状態 (SOC) を推定します。バッテリーは非線形システムであると仮定し、アンセンテッド カルマン フィルターを使って SOC を推定します。バッテリーの容量は各放電サイクルごとに低下するため、SOC の推定値が不正確になります。イベントベースの線形カルマン フィルターを使用して、バッテリーが充電状態から放電状態に切り替わるときにバッテリー容量を推定します。次に、推定された容量を使用してバッテリーの健全性を示します。
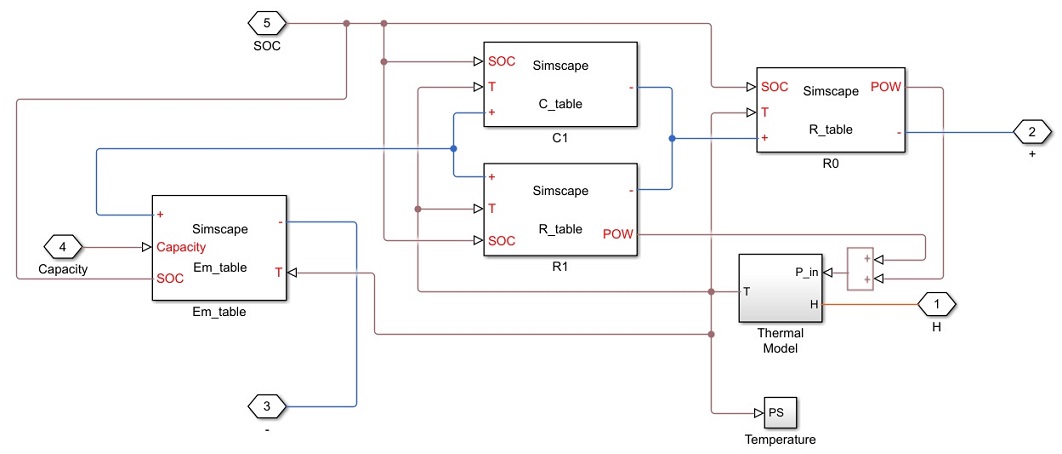
Simulink モデルは、バッテリー モデル、Unscented Kalman Filter ブロック、イベントベースの Kalman Filter ブロックの 3 つの主要コンポーネントを含みます。
open_system('BatteryExampleUKF/')
バッテリー モデル
Simscape ソフトウェアを使用して熱効果のあるバッテリー モデルを実装します。
バッテリー モデルの状態遷移の方程式は次のようになります。

ここで、 と
と  は RC ブロック内の熱および SOC 依存の抵抗とコンデンサ、
は RC ブロック内の熱および SOC 依存の抵抗とコンデンサ、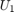 はコンデンサ
はコンデンサ  にかかる電圧、
にかかる電圧、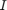 は入力電流、
は入力電流、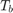 はバッテリーの温度、
はバッテリーの温度、 はバッテリーの容量 (単位: Ah)、
はバッテリーの容量 (単位: Ah)、 はプロセス ノイズです。
はプロセス ノイズです。
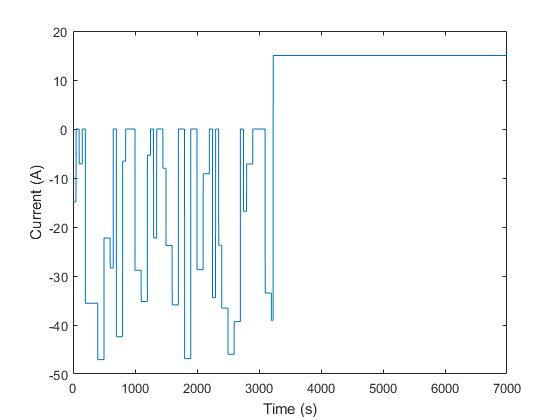
入力電流は、バッテリーの放電時はランダムに生成されたパルス、バッテリーの充電時は一定です。
測定方程式は以下で与えられます。
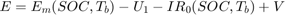
ここで、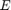 は測定された出力電圧、
は測定された出力電圧、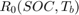 は直列抵抗、
は直列抵抗、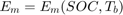 は電圧源からの起電力、
は電圧源からの起電力、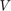 は測定ノイズです。
は測定ノイズです。
モデル内では 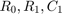 と
と 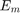 が 2 次元のルックアップ テーブルで、SOC とバッテリーの温度に依存します。ルックアップ テーブルのパラメーターは、実験データを使用して特定されます [1]。
が 2 次元のルックアップ テーブルで、SOC とバッテリーの温度に依存します。ルックアップ テーブルのパラメーターは、実験データを使用して特定されます [1]。
充電状態 (SOC) の推定
Unscented Kalman Filter ブロックを使用するには、MATLAB® 関数または Simulink 関数を使用して測定関数と状態遷移関数を指定します。この例では Simulink 関数を使用する方法を示します。アンセンテッド カルマン フィルターは離散時間フィルターであるため、最初に状態方程式を離散化します。この例ではオイラー法による離散化を使用します。サンプリング時間を 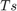 とします。一般的な非線形システム
とします。一般的な非線形システム 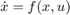 に対して、システムは次のように離散化できます。
に対して、システムは次のように離散化できます。

非線形バッテリー システムの状態ベクトルは次のとおりです。
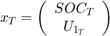 .
.
オイラー法による離散化を適用すると、次の方程式が得られます。

離散化された状態遷移方程式は、batteryStateFcn という Simulink 関数に実装されます。関数入力 x は状態ベクトルで、関数出力 xNext は、離散化した状態遷移方程式を使って求められた次のステップでの状態ベクトルです。関数では、x と xNext の信号の次元とデータ型を指定する必要があります。この例では、x と xNext の信号の次元は 2、データ型は double です。batteryStateFcn への追加の入力は、温度、推定容量、および電流です。追加の入力は状態遷移方程式への入力であり、Unscented Kalman Filter ブロックでは必須でない点に注意してください。
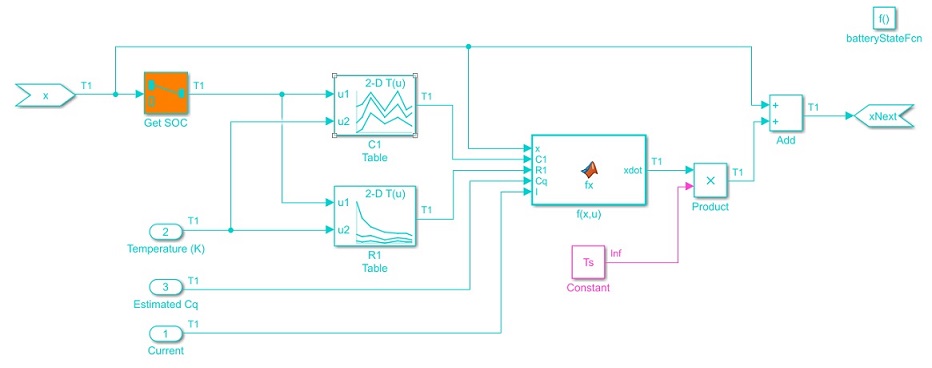
同様に、測定関数も batteryMeasurementFcn という Simulink 関数に実装されます。

Unscented Kalman Filter ブロックのパラメーターを次のように設定します。
[システム モデル] タブで、ブロック パラメーターを次のように指定します。
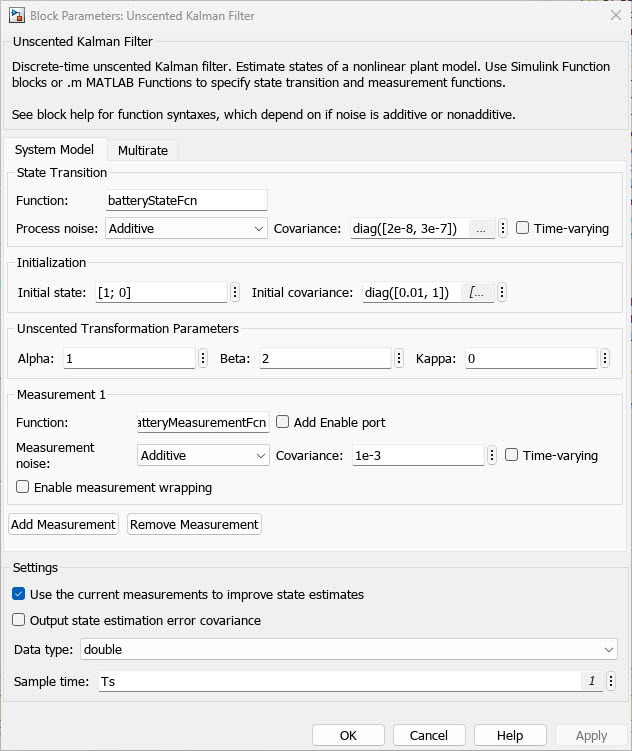
次のパラメーターを指定します。
状態遷移の関数:
batteryStateFcn。
離散化された状態遷移方程式を実装する、以前に定義した Simulink 関数の名前。
プロセス ノイズ: 時不変共分散
![$\left[ \begin{array}{cc} 2e-8 & 0 \\ 0 & 3e-7 \end{array} \right]$](../../examples/control/win64/NonlinearStateEstimationOfADegradingBatterySystemExample_eq13447715808488835843.png) をもつ
をもつ Additive。Additiveは、ノイズ項が最終信号に直接加算されることを意味します。
SOC および 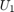 のプロセス ノイズは、バッテリー システムの動的な特性に基づいて推定されます。バッテリーは定格容量が 30 Ah で、放電サイクルまたは充電サイクルにおける電流の振幅が平均して 15A です。したがって、1 度の放電処理または充電処理に約 2 時間 (7200 秒) かかります。最大変化量は SOC で 100%、
のプロセス ノイズは、バッテリー システムの動的な特性に基づいて推定されます。バッテリーは定格容量が 30 Ah で、放電サイクルまたは充電サイクルにおける電流の振幅が平均して 15A です。したがって、1 度の放電処理または充電処理に約 2 時間 (7200 秒) かかります。最大変化量は SOC で 100%、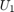 で約 4 ボルトです。
で約 4 ボルトです。
SOC と 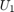 のステップあたりの最大変化量は、それぞれ
のステップあたりの最大変化量は、それぞれ 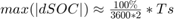 と
と 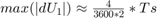 です。ここで
です。ここで 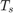 はフィルターのサンプリング時間です。この例では
はフィルターのサンプリング時間です。この例では 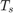 が 1 秒に設定されます。
が 1 秒に設定されます。
したがって、プロセス ノイズ  は次のようになります。
は次のようになります。
![$ W = \left[ \begin{array}{cc} (max(|dSOC|))^2 & 0 \\ 0 & (max(|dU_1|))^2 \end{array} \right] \approx \left[ \begin{array}{cc} 2e-8 & 0 \\ 0 & 3e-7 \end{array} \right] $](../../examples/control/win64/NonlinearStateEstimationOfADegradingBatterySystemExample_eq09064165382790124354.png) .
.
初期状態:
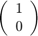 。
。
SOC の初期値は 100% (満充電のバッテリー) と仮定され、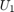 の初期値は 0 に設定されます。これは、
の初期値は 0 に設定されます。これは、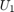 の事前情報がないためです。
の事前情報がないためです。
初期共分散:
初期の共分散は初期推定値の正確さと信頼度を示します。初期推定値の最大誤差は、SOC で 10%、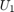 で 1 V であると仮定します。初期共分散行列は
で 1 V であると仮定します。初期共分散行列は ![$ \left[ \begin{array}{cc} 0.01 & 0 \\ 0 & 1 \end{array} \right] $](../../examples/control/win64/NonlinearStateEstimationOfADegradingBatterySystemExample_eq00624807450018571446.png) に設定されます。
に設定されます。
Unscented 変換のパラメーター:パラメーターは [2] に基づいて指定されます。
- Alpha: 1. Determine the spread of sigma points around x. Set Alpha to be 1 for larger spread.
- Beta: 2. Used to incorporate prior knowledge of the distribution. The nominal value for Beta is 2.
- Kappa: 0. Secondary scaling parameter. The nominal value for Kappa is 0.測定の関数:
batteryMeasurementFcn。
測定関数を実装する、以前に定義した Simulink 関数の名前。
測定ノイズ: 時不変共分散 1e-3 の
Additive。
測定ノイズ V は、測定機器の精度に基づいて推定されます。バッテリー電圧を測定する電圧計の精度は約 1% です。バッテリーの電圧は約 4V です。同じことが、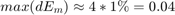 で表されます。したがって、
で表されます。したがって、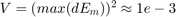 となります。
となります。
サンプル時間:
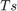 。
。
バッテリーの劣化の推定
バッテリーの劣化は減少する容量  によってモデル化されます。この例では、劣化の影響を示すため、バッテリーの容量が放電/充電サイクルごとに 1 Ah 減少するように設定されています。容量の劣化率が事前にわかっていないので、
によってモデル化されます。この例では、劣化の影響を示すため、バッテリーの容量が放電/充電サイクルごとに 1 Ah 減少するように設定されています。容量の劣化率が事前にわかっていないので、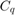 の状態方程式をランダム ウォークに設定します。
の状態方程式をランダム ウォークに設定します。
 ,
,
ここで、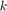 は放電/充電サイクルの数、
は放電/充電サイクルの数、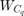 はプロセス ノイズです。
はプロセス ノイズです。
バッテリーは容量が 30% になると自動的に充電され、容量が 90% になると放電に切り替わるように設定されています。この情報を使用して、電流 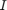 を 1 回の充電サイクルまたは放電サイクルで積分し、バッテリーの容量を測定します (クーロン カウンター)。
を 1 回の充電サイクルまたは放電サイクルで積分し、バッテリーの容量を測定します (クーロン カウンター)。
 の測定方程式は次のとおりです。
の測定方程式は次のとおりです。
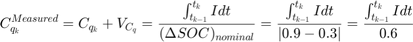
ここで、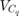 は測定ノイズです。
は測定ノイズです。
バッテリーの劣化の状態遷移と測定方程式は、次の状態空間形式にすることができます。
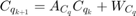
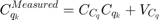
ここで、 と
と 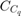 は 1 に等しくなります。
は 1 に等しくなります。
上記の線形システムについて、カルマン フィルターを使ってバッテリーの容量を推定します。線形カルマン フィルターから推定された  を使用して、SOC の推定を改善します。この例では、イベントベースの線形カルマン フィルターを使って
を使用して、SOC の推定を改善します。この例では、イベントベースの線形カルマン フィルターを使って  を推定します。
を推定します。 は充電サイクルまたは放電サイクルごとに 1 回測定されるので、線形カルマン フィルターが有効になるのは充電または放電の終了時のみです。
は充電サイクルまたは放電サイクルごとに 1 回測定されるので、線形カルマン フィルターが有効になるのは充電または放電の終了時のみです。
ブロック パラメーターを以下のように設定します。
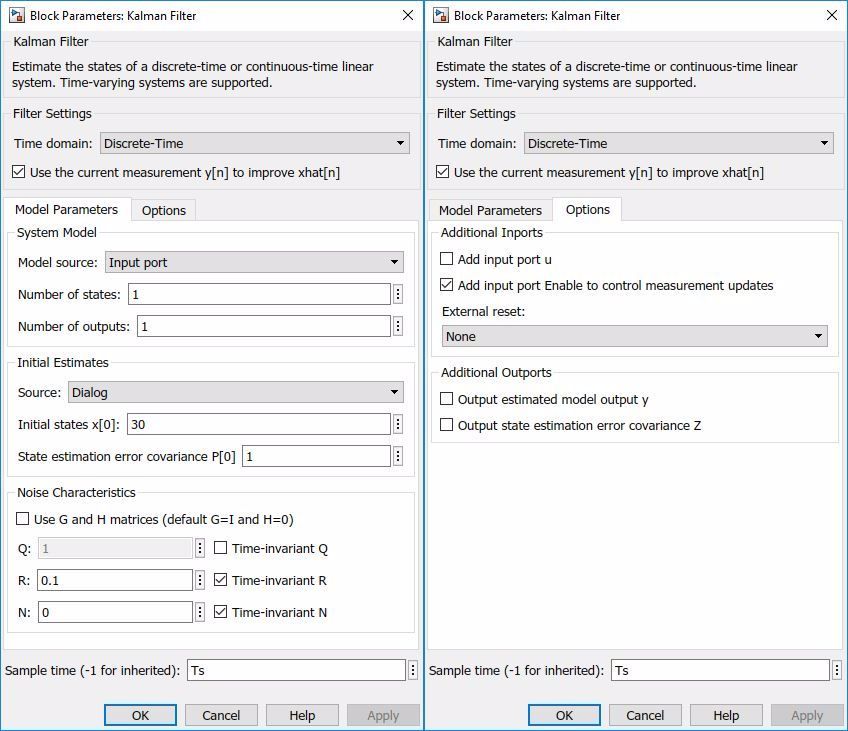
[モデル パラメーター] タブで、プラント モデルとノイズ特性を指定します。
モデルソース:
Input Port。
イベントベースのカルマン フィルターを実装するため、イベントが発生した場合にのみ状態方程式が有効になります。つまり、状態方程式もイベントベースです。線形システム 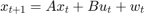 に対し、状態方程式を次のように設定します。
に対し、状態方程式を次のように設定します。
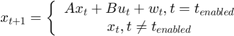 .
.
A:
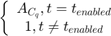 。この例では、
。この例では、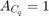 となります。したがって、
となります。したがって、 は常に 1 に等しくなります。
は常に 1 に等しくなります。
C: 1。ここで、
 。
。
初期推定の [ソース]:
Dialog。Initial state x[0]に初期状態を指定します。
初期状態 x[0]: 30。これはバッテリーの定格容量 (30Ah) です。
Q:

これはプロセス ノイズ 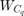 の共分散です。容量の低下率は放電/充電サイクルごとに約 1 Ah なので、プロセス ノイズを 1 に設定します。
の共分散です。容量の低下率は放電/充電サイクルごとに約 1 Ah なので、プロセス ノイズを 1 に設定します。
R: 0.1。これは測定ノイズ
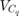 の共分散です。容量の測定誤差は 1% 未満であると仮定します。バッテリーの容量が 30 Ah の場合、測定ノイズは
の共分散です。容量の測定誤差は 1% 未満であると仮定します。バッテリーの容量が 30 Ah の場合、測定ノイズは 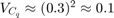 です。
です。
サンプル時間: Ts。
[オプション] タブで、入力端子 Enable を追加して測定値の更新を制御します。イネーブル端子は、バッテリー容量の推定値を連続して更新するのではなく、充電イベントまたは放電イベントにおいて更新するために使用されます。
Enable を 0 に設定しても、状態方程式を使用した予測はディセーブルにならない点に注意してください。したがって、状態方程式もイベントベースとして設定されます。Kalman Filter ブロックにイベントベースの A と Q を設定することにより、Enable が 0 に設定されると、状態方程式を使用する予測がディセーブルになります。
結果
システムをシミュレートするには、ファイル BatteryParameters.mat に保存されているバッテリーのパラメーターを読み込みます。このファイルには 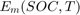 、
、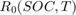 、
、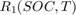 などのバッテリー パラメーターが含まれています。
などのバッテリー パラメーターが含まれています。
load BatteryParameters.mat
システムをシミュレートします。
sim('BatteryExampleUKF')
各タイム ステップで、アンセンテッド カルマン フィルターが電圧測定値 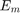 に基づいて SOC の推定値を提供します。実際の SOC、推定された SOC、およびその差異をプロットします。
に基づいて SOC の推定値を提供します。実際の SOC、推定された SOC、およびその差異をプロットします。
% Synchronize two time series [RealSOC, EstimatedSOC] = synchronize(RealSOC, EstimatedSOC, 'intersection'); figure; subplot(2,1,1) plot(100*RealSOC,'b','LineWidth',1.5); hold on plot(100*EstimatedSOC,'r--','LineWidth',1); title('State of Charge'); xlabel('Time (s)'); ylabel('SOC (%)'); legend('Actual','UKF estimate','Location','Best','Orientation','horizontal'); axis tight subplot(2,1,2) DiffSOC = 100*(RealSOC - EstimatedSOC); plot(DiffSOC.Time, DiffSOC.Data, 'LineWidth', 1.5); xlabel('Time(s)'); ylabel('\Delta SOC (%)','Interpreter','Tex'); legend('Difference between Real SOC and Estimated SOC','Location','Best') axis tight
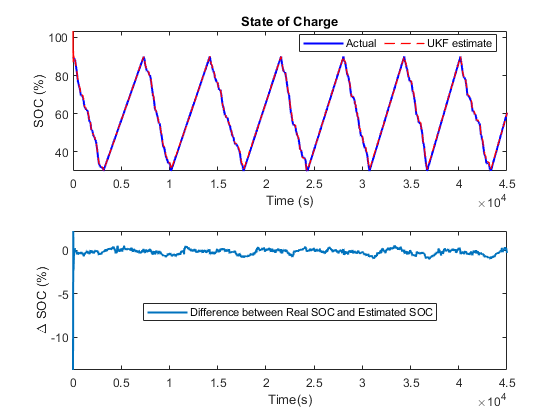
初期推定誤差の後、SOC は実際の SOC へと迅速に収束します。最終の推定誤差は 0.5% 内です。したがって、アンセンテッド カルマン フィルターにより SOC を正確に推定できます。
放電/充電の各遷移において、SOC の推定を改善するためにバッテリーの容量が推定されます。バッテリー システムはインジケーター信号を出力してバッテリーの現在の処理を通知します。放電処理はインジケーター信号で -1 として表され、充電処理は 1 で表されます。この例では、容量の推定にカルマン フィルターをイネーブルにするかディセーブルにするかを判定するためにインジケーター信号の変化が使用されます。実際の容量と推定された容量、および充電/放電のインジケーター信号をプロットします。
figure; subplot(2,1,1); plot(RealCapacity,'b','LineWidth',1.5); hold on plot(EstimatedCapacity,'r--','LineWidth',1.5); xlabel('Time (s)'); ylabel('Capacity (Ah)'); legend('Actual','KF estimate','Location','Best'); subplot(2,1,2); plot(DischargeChargeIndicator.Time,DischargeChargeIndicator.Data,'b','LineWidth',1.5); xlabel('Time(s)'); ylabel('Enable Signal');

一般に、カルマン フィルターを使用して実際の容量を追跡することが可能です。容量の推定値と実際の値の間には 1/2 サイクルの遅延があります。これは、バッテリーの容量低下は完全な放電/充電サイクルが 1 度終了してから始まるためです。最後の放電または充電サイクルの容量測定値はクーロン カウンター方式によって提供されます。
まとめ
この例では、Unscented Kalman Filter ブロックを使用してリチウム電池の非線形の状態推定を行う方法を説明しています。また、バッテリーの容量を推定するためのイベントベースのカルマン フィルターを開発する手順も示されています。新しく推定された容量は、アンセンテッド カルマン フィルターでの SOC の推定を改善するために使用されます。
参考文献
[1] Huria, Tarun, et al."High fidelity electrical model with thermal dependence for characterization and simulation of high power lithium battery cells."Electric Vehicle Conference (IEVC), 2012 IEEE International.IEEE, 2012.
[2] Wan, Eric A., and Rudolph Van Der Merwe."The unscented Kalman filter for nonlinear estimation."Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000.AS-SPCC.The IEEE 2000.Ieee, 2000.
参考
Extended Kalman Filter | Unscented Kalman Filter | Particle Filter