複数のマルチレートセンサーをもつ非線形システムの状態の推定

この例では次を使用します。

この例では、さまざまなサンプルレートで動作する複数のセンサーをもつシステムについて Simulink™ で非線形の状態推定を行う方法を示します。Control System Toolbox™ の Extended Kalman Filter ブロックは、GPS およびレーダーの測定値を使用してオブジェクトの位置と速度を推定するために使用されます。

はじめに

ツールボックスには非線形の状態推定を行うための Simulink ブロックが 3 つあります。

Extended Kalman Filter: 1 次離散時間の拡張カルマンフィルターアルゴリズムを実装します。
Unscented Kalman Filter: 離散時間のアンセンテッドカルマンフィルターアルゴリズムを実装します。
Particle Filter: 離散時間の粒子フィルターアルゴリズムを実装します。

これらのブロックは、さまざまなサンプルレートで動作する複数のセンサーを使用した状態推定をサポートします。これらのブロックの使用に関する一般的なワークフローは次のとおりです。

MATLAB または Simulink 関数を使用してプラントとセンサーの動作をモデル化します。
ブロックのパラメーターを構成します。
フィルターをシミュレートして結果を解析し、フィルターの性能の信頼度を得ます。
ハードウェアにフィルターを展開します。Simulink Coder™ ソフトウェアを使用して、これらのフィルターのコードを生成できます。

この例では、Extended Kalman Filter ブロックを使用し、このワークフローの最初の 2 つの手順を示します。最後の 2 つの手順については「次のステップ」の節で簡単に説明します。この例の目標は、レーダーおよび GPS センサーから提供されたノイズを含む測定値を使用してオブジェクトの状態を推定することです。オブジェクトの状態とはその位置と速度であり、Simulink モデル内では xTrue で表されます。

Particle Filter ブロックに関心がある場合、「Particle Filter ブロックを使用した Simulink でのパラメーターおよび状態の推定」の例を参照してください。

プラントのモデル化

拡張カルマンフィルター (EKF) アルゴリズムには、タイムステップ間の状態の変化を記述する状態遷移関数が必要です。このブロックは次の 2 つの関数形式をサポートしています。

加法性のプロセスノイズ:
非加法性のプロセスノイズ:

ここで、f(..) は状態遷移関数、x は状態、w はプロセスノイズです。u はオプションで、f に対する追加入力を表しています (たとえば、システム入力やパラメーター)。加法性ノイズは、次の状態とプロセスノイズが線形的に関係していることを意味します。関係が非線形である場合は、非加法性の形式を使用します。

関数 f(...) は MATLAB Coder™ の制限に準拠する MATLAB 関数か、Simulink Function ブロックにすることができます。f(...) の作成後、関数名と、Extended Kalman Filter ブロックのプロセスノイズが加法性と非加法性のどちらであるかを指定します。

この例では、北方向および東方向の位置と、オブジェクトの 2 次元平面における速度を追跡しています。推定された量は次のとおりです。

$\hat{x}[k] = \left[
 \begin{array}{c}
 \hat{x}_e[k] \\
 \hat{x}_n[k] \\
 \hat{v}_e[k] \\
 \hat{v}_n[k]
 \end{array}
 \right]
 \;
\begin{array} {ll}
\textnormal{East position estimate} \; [m] \\
\textnormal{North position estimate} \; [m] \\
\textnormal{East velocity estimate} \; [m/s] \\
\textnormal{North velocity estimate} \; [m/s] \\
\end{array}$

ここでは離散時間インデックスです。使用される状態遷移方程式は非加法性形式 $\hat{x}[k+1] = A\hat{x}[k] + Gw[k]$ であり、 $\hat{x}$ は状態ベクトル、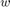はプロセスノイズです。フィルターでは、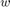はゼロ平均で、既知の分散をもつ独立の確率変数であると仮定します。行列 A および行列 G は次のとおりです。

$A = \left[
 \begin{array}{c c c c}
 1 & 0 & T_s & 0 \\
 0 & 1 & 0 & T_s \\
 0 & 0 & 1 & 0 \\
 0 & 0 & 0 & 1
 \end{array}
 \right]
 \;\;\;\;\;\;\;\; G = \left[
 \begin{array}{c c}
 T_s/2 & 0 \\
 0 & T_s/2 \\
 1 & 0 \\
 0 & 1
 \end{array}
 \right]
$

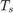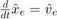ここではサンプル時間になります。A および G の 3 行目は、ランダムウォーク $\hat{v}_e[k+1]=\hat{v}_e[k]+w_1[k]$ として東方向の速度をモデル化しています。実際は、位置は連続時間変数であり、経時的速度 $\frac{d}{dt}\hat{x}_e=\hat{v}_e$ の積分となります。A および G の 1 行目は、この運動学的関係 $(\hat{x}_e[k+1]-\hat{x}_e[k])/T_s = (\hat{v}_e[k+1]+\hat{v}_e[k])/2$ の離散近似を表します。A および G の 2 行目と 4 行目は、北方向の速度と位置の間の同じ関係を表します。この状態遷移モデルは線形ですが、レーダー測定値のモデルは非線形です。この非線形性のため、拡張カルマンフィルターなどの非線形の状態推定器の使用が必要になります。

この例では Simulink Function ブロックを使用して状態遷移関数を実装します。そのためには以下を行います。

Simulink Function ブロックを Simulink/User-Defined Functions ライブラリからモデルに追加します。
Simulink Function ブロックに示された名前をクリックします。必要に応じて、関数名を編集し、入力引数と出力引数を追加または削除します。この例では状態遷移関数の名前は stateTransitionFcn です。1 つの出力引数 (xNext) と、2 つの入力引数 (x と w) があります。

この例では必要ありませんが、Simulink Function 内で Simulink モデルの残りの部分からの任意の信号を使用できます。そのためには、Simulink/Sources ライブラリから Inport ブロックを追加します。これらは、関数のシグネチャを介して設定される ArgIn ブロックおよび ArgOut ブロックとは異なります (xNext = stateTransitionFcn(x, w))。
Simulink Function ブロックで、Simulink ブロックを使用して関数を作成します。
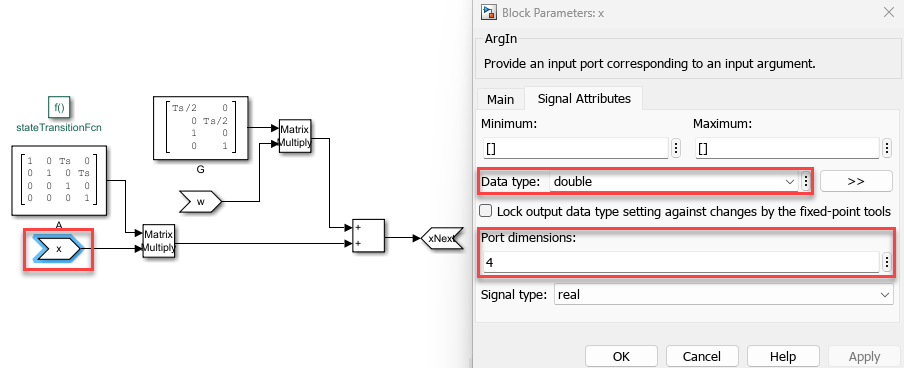
入力引数と出力引数 x、w および xNext の次元を、ArgIn ブロックおよび ArgOut ブロックの [信号属性] タブで設定します。データ型と端子の次元は、Extended Kalman Filter ブロックで指定した情報と同じでなければなりません。

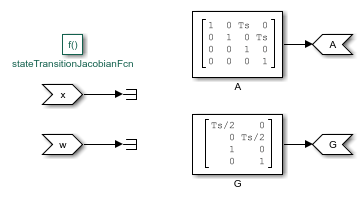
この例では状態遷移関数の解析ヤコビアンも実装されています。ヤコビアンの指定はオプションです。ただし、これによって計算負荷が軽減され、大半の場合は状態推定の精度を高めることができます。状態遷移関数は Simulink 関数であるため、ヤコビ関数を Simulink 関数として実装します。

open_system('multirateEKFExample')
open_system('multirateEKFExample/Simulink Function - State Transition Jacobian');

センサーのモデル化 - レーダー

Extended Kalman Filter ブロックには、状態と測定値の関係を記述する測定関数も必要です。次の 2 つの関数形式がサポートされます。

加法性の測定ノイズ:
非加法性の測定ノイズ:

ここで、h(..) は測定関数、v は測定ノイズです。u はオプションで、h に対する追加入力を表しています (たとえば、システム入力やパラメーター)。これらの入力は、状態遷移関数の入力とは異なるものを指定できます。

この例では原点に位置するレーダーがオブジェクトの範囲と角度を 20 Hz で測定します。両方の測定値が約 5% のノイズを含むと仮定します。これは次の測定方程式によってモデル化できます。

$y_{radar}[k] = \left[
 \begin{array}{c}
 \sqrt{x_n[k]^2+x_e[k]^2} \; (1+v_1[k]) \\
 atan2(x_n[k], x_e[k]) \; (1+v_2[k]) \\
 \end{array}
 \right]
$

ここでとは測定ノイズ項で、それぞれが分散 0.05^2 をもちます。すなわち、測定値の大部分で誤差が 5% 未満になります。とは測定値に単純に加算されるのではなく状態 x に依存するため、測定ノイズは非加法性です。この例では、レーダーの測定方程式が Simulink Function ブロックを使用して実装されます。

open_system('multirateEKFExample/Simulink Function - Radar Measurements');

センサーのモデル化 - GPS

GPS は、オブジェクトの東方向および北方向の位置を 1 Hz で測定します。したがって、GPS センサーの測定方程式は次のようになります。

$y_{GPS}[k] = \left[
 \begin{array}{c}
 x_e[k] \\
 x_n[k]
 \end{array}
 \right] +
 \left[
 \begin{array}{c}
 v_1[k] \\
 v_2[k]
 \end{array}
 \right]
$

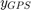ここでとは、共分散行列 [10^2 0; 0 10^2] をもつ測定ノイズ項です。したがって、測定値の誤差は約 10 メートルであり、誤差は無相関です。ノイズ項が測定値 $y_{GPS}$ に線形の影響を与えるので、この測定ノイズは加法性です。

この関数を作成し、gpsMeasurementFcn.m という名前のファイルに保存します。測定ノイズが加法性の場合、関数内にノイズ項を指定することはできません。この関数名と測定ノイズ共分散を、Extended Kalman Filter ブロック内で提供します。

type gpsMeasurementFcn

function y = gpsMeasurementFcn(x)
% gpsMeasurementFcn GPS measurement function for state estimation
%
% Assume the states x are:
%   [EastPosition; NorthPosition; EastVelocity; NorthVelocity]

%#codegen

% The %#codegen tag above is needed is you would like to use MATLAB Coder to 
% generate C or C++ code for your filter

y = x([1 2]); % Position states are measured
end

フィルター構築

推定を実行する Extended Kalman Filter ブロックを設定します。状態遷移と測定の関数名、初期状態および状態誤差の共分散、プロセスノイズと測定ノイズの特性をそれぞれを指定します。

ブロックダイアログの [システムモデル] タブで、次のパラメーターを指定します。

状態遷移

[関数] に状態遷移関数 stateTransitionFcn を指定します。この関数のヤコビアンがあるので、[ヤコビアン] を選択して、ヤコビ関数 stateTransitionJacobianFcn を指定します。
プロセスノイズが状態に与える影響を関数で明示的に宣言したので、[プロセスノイズ] ドロップダウンリストで Nonadditive を選択します。
プロセスノイズの共分散を [0.2 0; 0 0.2] に指定します。この例の「プラントのモデル化」の節で説明されているように、プロセスノイズ項は各方向における速度のランダムウォークを定義します。対角項は、状態遷移関数の 1 つのサンプル時間において可能なおおよその速度の変化量を捉えるものです。非対角項はゼロに設定されます。これは北方向と東方向の速度の変化が無相関であるという単純な仮定を表します。

初期化

[初期状態] に最良の初期状態推定を指定します。この例では [100; 100; 0; 0] を指定します。
[初期の共分散] に状態推定の信頼度を指定します。この例では 10 を指定します。ソフトウェアはこの値を、真の状態値がおそらく初期推定値から 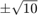$\pm\sqrt{10}$ 以内にあるとして解釈します。Initial covariance をベクトルとして設定することで、状態ごとに個別の値を指定できます。行列として指定すると、この不確かさの相互相関を指定できます。

センサーが 2 つあるので、[測定値の追加] をクリックして 2 番目の測定関数を指定します。

測定 1

[関数] に、測定関数の名前 radarMeasurementFcn を指定します。
プロセスノイズが状態に与える影響を関数で明示的に宣言したので、[測定ノイズ] ドロップダウンリストで Nonadditive を選択します。
「センサーのモデル化 - レーダー」の節で説明されているように、測定ノイズの共分散を [0.05^2 0; 0 0.05^2] に指定します。

測定 2

[関数] に、測定関数の名前 gpsMeasurementFcn を指定します。
このセンサーモデルは加法性ノイズを含みます。したがって、[測定ノイズ] ドロップダウンリストで GPS 測定ノイズを Additive に指定します。
測定ノイズ共分散を [100 0; 0 100] に指定します。

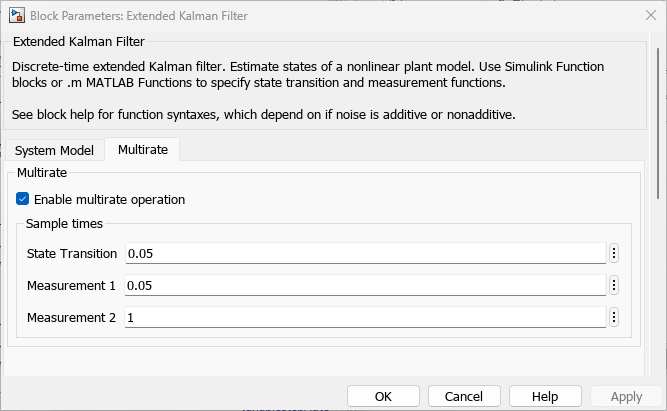
2 つのセンサーは異なるサンプルレートで動作するため、[マルチレート] タブで次の構成を行います。

Enable multirate operation を選択します。
状態遷移のサンプル時間を指定します。状態遷移のサンプル時間は最小でなければならず、すべての測定サンプル時間は状態遷移サンプル時間の整数倍でなければなりません。[状態遷移] のサンプル時間を、最速測定のサンプル時間である 0.05 に指定します。この例では必要ありませんが、すべての測定値よりも小さいサンプル時間を状態遷移に指定することも可能です。その場合、測定値のないサンプル時間が発生する可能性があります。これらのサンプル時間についてはフィルターが状態遷移関数を使って状態の予測を生成します。
[測定 1] のサンプル時間 (レーダー) を 0.05 秒、[測定 2] (GPS) を 1 秒に指定します。

シミュレーションと結果

オブジェクトが次の操縦方法によって正方形のパターンで移動するシナリオをシミュレートして、拡張カルマンフィルターの性能をテストします。

t = 0 でオブジェクトが $x_e(0)=100\; \textnormal{[m]}, x_n(0)=100 \;\textnormal{[m]}$ から開始します。
t = 20 秒までは $\dot{x}_n=50\;\textnormal{[m/s]}$ で北方向に移動します。
t = 20 から t = 45 秒の間は $\dot{x}_n=40\;\textnormal{[m/s]}$ で東方向に移動します。
t = 45 から t = 85 秒の間は $\dot{x}_n=-25\;\textnormal{[m/s]}$ で南方向に移動します。
t = 85 から t = 185 秒の間は $\dot{x}_e=-10\;\textnormal{[m/s]}$ で西方向に移動します。

この動きに対応する真の状態値を生成します。

Ts = 0.05; % [s] Sample rate for the true states
[t, xTrue] = generateTrueStates(Ts); % Generate position and velocity profile over 0-185 seconds

モデルのシミュレーションを実行します。たとえば、東方向における実際の速度と推定速度を見てみましょう。

sim('multirateEKFExample');
open_system('multirateEKFExample/Scope - East Velocity');

プロットには、東方向における真の速度と拡張カルマンフィルターによる速度の推定値が表示されます。フィルターは速度の変化を正しく追跡しています。フィルターがマルチレートであることは、t が 20 ～ 30 秒の時間範囲で最も顕著です。フィルターは毎秒 (GPS サンプルレート) ごとに大幅な修正を行いますが、レーダー測定による修正は 0.05 秒ごとに見られます。

次のステップ

状態推定の検証: アンセンテッドまたは拡張カルマンフィルターのパフォーマンス検証は、通常は幅広いモンテカルロ法シミュレーションを使用して実行されます。詳細については、Simulink でのオンライン状態推定の検証を参照してください。
コードの生成: Unscented Kalman Filter ブロックと Extended Kalman Filter ブロックは、Simulink Coder™ ソフトウェアを使用した C および C++ コードの生成をサポートします。これらのブロックに提供する関数は、MATLAB Coder™ ソフトウェア (MATLAB 関数を使用してシステムをモデル化している場合) および Simulink Coder ソフトウェア (Simulink Function ブロックを使用してシステムをモデル化している場合) の制限に準拠しなければなりません。