数値および調整可能なコンポーネントの両方をもつ制御システムモデル

この例では、固定されたプラントとセンサーダイナミクスおよび調整可能な制御コンポーネントの両方をもつ制御システムの調整可能モデルを作成する方法を示します。

次の図の制御システムについて考えます。

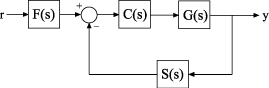
プラント応答は $G (s) = 1 / (s + 1)^{2}$ で、センサーダイナミクスのモデルは $S (s) = 5 / (s + 4)$ であると仮定します。コントローラー $C$ は調整可能な PID コントローラーであり、プレフィルター $F = a / (s + a)$ は 1 つの調整可能なパラメーター a をもつローパスフィルターです。

プラントとセンサーダイナミクスを表すモデルを作成します。プラントとセンサーダイナミクスは固定なので、それらを数値 LTI モデルで表します。

G = zpk([],[-1,-1],1);
S = tf(5,[1 4]);

調整可能なコンポーネントをモデル化するには、制御設計ブロックを使用します。コントローラー C の調整可能な表現を作成します。

C = tunablePID('C','PID');

C は tunablePID オブジェクトであり、事前定義された比例-積分-微分 (PID) 構造をもつ制御設計ブロックです。

1 つの調整可能なパラメーターをもつフィルター $F = a / (s + a)$ のモデルを作成します。

a = realp('a',10); 
F = tf(a,[1 a]);

a は、初期値 10 の realp (調整可能な実数パラメーター) オブジェクトです。a を tf 内の係数として使用すると、調整可能な genss モデルオブジェクト F が作成されます。

モデルを相互接続して r から y への完全な閉ループ応答のモデルを作成します。

T = feedback(G*C,S)*F

T =

  Generalized continuous-time state-space model with 1 outputs, 1 inputs, 5 states, and the following blocks:
    C: Tunable PID controller, 1 occurrences.
    a: Scalar parameter, 2 occurrences.

Type "ss(T)" to see the current value, "get(T)" to see all properties, and "T.Blocks" to interact with the blocks.

T は genss モデルオブジェクトです。数値 LTI モデルのみを接続することによって形成される統合モデルとは対照的に、T は制御システムの調整可能な要素を記録しています。調整可能な要素は、genss モデルオブジェクトの Blocks プロパティに格納されます。T の調整可能な要素を調べます。

T.Blocks

ans = struct with fields:
    C: [1x1 tunablePID]
    a: [1x1 realp]

調整可能なコンポーネントをもつ制御システムの genss モデルを作成する場合は、systune などの調整コマンドを使用して、指定した設計要件を満たすように自由パラメーターを調整できます。

参考

feedback | tunablePID

数値および調整可能なコンポーネントの両方をもつ制御システム モデル

参考

関連するトピック

数値および調整可能なコンポーネントの両方をもつ制御システムモデル