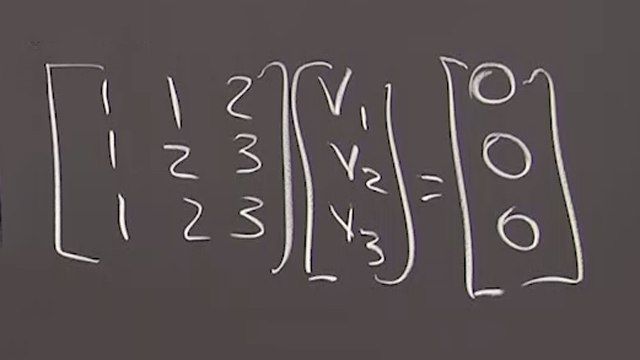Differential Equations and Linear Algebra, 3.3d: The Tumbling Box in 3-D
From the series: Differential Equations and Linear Algebra
Gilbert Strang, Massachusetts Institute of Technology (MIT)
A box in the air can rotate around its shortest and longest axes. Around the middle axis it tumbles wildly.
Published: 27 Jan 2016
OK. Here's an example that's more or less for fun. Because you'll see me try to do it. You can do it better. I call the problem the tumbling blocks. Only in this example, in my demonstration, it's going to be a tumbling book.
I'm going to take a book, the sacred book, and throw it in the air. And I'll throw it three different ways. And the question is, is the spinning book stable or not? And let me tell you the three ways and then give you the three equations that came from Euler.
So those are the three equations. You see that they're not linear. And those are for the angular momentum. So there's a little physics behind the equations. But for us, those are the three equations.
So the first throw will spin around the very short axis, just the thickness of the book, maybe an inch. So when I toss that, as I'll do now, you will see if I can toss it not too nervously I hope. It came-- it was stable. The book came back to me without wobbling.
Of course, my nerves would give it a little wobble, and that wobble would continue. It will be only neutrally stable. The wobble doesn't disappear. But it doesn't grow into a tumble. OK. So that's one axis, the short axis.
Then I'll throw it also around the long axis, flipped like this. I think that will be stable too. And then, finally, on the intermediate axis, is middle length axis. Notice the rubber band that's holding the book together. Holding so the pages don't open. And this, we'll see, I think, will be unstable.
And similarly, throwing a football, throwing other Frisbees, whatever your throw. Any 3D object has got these three axes: a short one, a medium one, and a long axis. And the equations will tell us short and long axes should give a stable turning. And the in between axis is unstable.
Well, how do we decide for our differential equation whether the fixed point, a fixed point, that's a critical point, a steady state-- we have to find this steady state, and then for each steady state we linearize. We find the derivatives at that steady state. And that gives us a constant matrix at that steady state. And then the eigenvalue is decided.
So first, find the critical points. Second, find the derivatives at the critical points. Third, for that matrix of derivatives, find the eigenvalues and decide stability. That's the sequence of steps. OK. The first time we've ever done a three by three matrix. Maybe the last time. OK.
Let me, before I start-- before I find the critical points-- notice some nice properties. If I multiply this equation by x, this one by y, this one by z, and add, those will add to 0. When there's an x there, a y there, and a z there, I get a 1 minus 2 and a 1 they add to 0. So x times dx dt. y times dy dt. z time dz dt adds to 0.
That's an important fact. That's telling me that the derivative of something is 0. That something will be a constant. So I'm seeing here the derivative of that whole business would be the derivative of a half probably. x squared, because the derivative of x squared will be with a half. The derivative will be x dx dt. And y squared and z squared is the derivative is 0. The derivative of that line is just this line. It's 0. So this is a constant.
No doubt, that's probably telling me that the total energy, the kinetic energy, is constant. After I've tossed that book up in the air, I'm not touching it. It's doing its thing. And it's not going to change energy because nothing is happening to it. It's just out there. Now there are other-- so that's a rather nice thing. This is a constant.
Now there's another way. If I multiply this one by 2x, and I multiply this one by y, and add just those two, that cancels. So 2x dx dt-- 2x times the first one-- and y times the second one gives 0. Again, I'm seeing something is constant. The derivative of something, and that something is x squared plus 1/2 y squared is a constant. Another nice fact. Another quantity that's conserved.
And as I'm flying around in space, this quantity x squared plus 1/2 y squared does not change. This sort of-- that involved all of xyz. And of course that's the equation of a sphere. So in energy space, or in an xyz space, our solution is wandering around a sphere. And this is the equation for, I guess, it's an ellipse. So there's an ellipse on that's sphere that it's actually staying on that ellipse.
And in fact there's another ellipse because I could've multiplied this one by 2z and this one by y and added. And then those would have canceled. Minus 2 xyz plus 2xyz. So that also tells me that it would be probably z squared plus 1/2 y squared equals a constant. That's another ellipse. z squared plus 1/2 y squared. You see this? If I take the derivative of that, I have 2z times dz dt plus y times dy dt. Adding give 0. The derivative is 0. The thing is a constant.
But! But, but, but! If I subtract this one from this one, take the difference of these two. Suppose I take this one minus this one. The 1/2 y squared will go. So that will tell me that x squared minus z squared is a constant. Oh, boy! I haven't solved my three equations. But I found out a whole lot about the solution. The solution stays on the sphere, wanders around somehow. It also at the same time stays on that ellipse. And it stays on that ellipse. But this is not an ellipse, not an ellipse. That's the equation of a hyperbola. And that's why-- which, of course, goes off to infinity. And that's why the-- well, it goes off to infinity, but it has to stay on the sphere. It wanders. This will be responsible for the unstable motion.
Professor --, who would do this far better than me, his great lecture in 1803, Differential Equations, was exactly this. The full hour to tell you everything about the tumbling box. So I'm going to do the demonstration and write down the main facts and understand the stability, the discussion of stability. I'm ready to move on to the discussion of stability.
Again, here are my three equations. We're up to three equation, so we're going have a three by three matrix. And first I have to find out the critical points, the steady states of this motion. How could I toss it so that if I toss it perfectly it stays exactly as tossed? And the answer is, around the axis.
If I toss this perfectly, with no nerves, it'll just spin exactly as I'm throwing it. The x, y, and z will all be constant. Now, when I toss it on that axis. I'm looking for-- here are my right hand side. YZ, minus 2XZ, and XY. And I wrote those in capital letters because those are going to be my steady states. Now I'm looking for are points where nothing's happened.
If those three right hand sides of the equation are 0, I'm not going to move. xyz will stay where they are. So can you see solutions of those three equations? Well, they're pretty special equations. I get a solution when, for example, solutions could be 1, 0, 0/
If two of the three-- if y and z are 0. y is 0, z is 0, y and z are 0, I get 0. So that is a certainly steady state. x equal 1, y and z equal 0 and 0. And that steady state is spinning around one axis. And, actually, I could have also a minus 1 would also be. So I've found, actually, two steady states with y and z 0. Then there'll be two more with x and z 0. And this could be-- that'll be spinning around the middle axis. And then 0, 0, 1 or minus 1, that would be spinning around the third axis, the long axis.
So those are my steady states. And I guess, come to think of it, 0, 0, 0 would also be a steady state. I think I found them all. These are the xy's. These are the x, y, z steady states. OK.
So now once you know the steady states, that's usually fun, as it was here. Now the slightly less fun step is find all the derivatives, find that Jacobian matrix of derivative. So I've got three equations. Three unknowns, xyz. Three right hand sides. And I have to find-- I'm going to have a three by three matrix of derivatives. This Jacobian matrix. So J for the Jacobian, the matrix of first derivatives.
So what goes into the matrix of first derivative? Let me write Jacobian. It is named after Jacoby. It's the matrix of first derivatives. On the top row are the derivatives of the first function with respect to x. Well, the derivative with respect to x is 0. The derivative with respect to y is z. The derivative with respect to z is y. Those were partial derivatives. They tell me how much the first unknown x moves. They tell me what's happening with the first unknown x around the critical point whichever it is.
OK. What about the partial derivatives from the second equation? it's partial derivatives will go into this row. So x has a minus 2z. y derivative is 0. z derivative is minus 2x. And the third one, the z derivative is 0 here. The y derivative in x. And the x derivative is y. I've found the 3 by 3 matrix with the nine partial first derivatives. OK.
It's the eigenvalues of that matrix at these points that decide stability. So I write that down. Eigenvalues of J at the critical points x, y, z that's what I need. That's what decides stability.
Let me just take the first critical point. What is my matrix? I have to figure out what is the matrix at that point? And I'll just take 1, 0, 0. 1, 0, 0. If x is 1-- so I'm getting, this is at the point x equal 1. y and z are 0. So if x is 1, then that that's a minus 2 and a 1. And I think everything else is 0.
So it'll be the eigenvalues of that matrix that decide the stability 1, 0, 0 of that fixed point. And remember, that's the toss around the narrow axis. That's the toss around the short axis. OK.
What about the eigenvalues of that matrix? Well, I can see here that really it's three by three. But really, with all those 0s, that gives me an eigenvalues of 0. So I'm going to have an eigenvalue of 0 here. And then I'm going to have eigenvalues from the part of that matrix, which is two by two. So I'll have a lambda equals 0 here. And two eigenvalues from here.
And I look at that, and what do I see? Now this is a two by two problem. I see the trace is 0. 0 plus 0. My eigenvalues are a plus and minus pair because they add to 0. They multiply to give the determinant. The determinant of that matrix is 2. The determinant of that matrix is 2. OK.
So it has a positive determinant. That's good for stability. But the trace is only 0. It's not quite negative. It's not positive. It's just at 0. So this is going to be a case of neutral stability. The eigenvalues will be-- I'll have a 0 eigenvalue from there. The eigenvalues from this two by two will be-- there'll be a square root of 2 times i and a minus the square root of 2 times i. I think those are the eigenvalues.
And what I see there is they're all imaginary. This is a pure oscillation. The wobbling keeps wobbling. Doesn't get worse. Doesn't go away. It's neutral stability at this point. So neutral stability is what we hopefully will see again. Yes. And I think, also, if I flip on the long axis. Good. Did you see that brilliant throw? It's neutral stability. It came back without doing anything too bad.
And I finally have to do the axis that we're all intensely waiting for, the middle axis. And the middle axis is when the book starts tumbling, and it's going to be a question of whether I can catch it or not. May I try? And then may I find-- what am I expecting on the neutral axis? I'm expecting instability. I think actually it will be a saddle point. But there'll be a positive eigenvalues.
There will be a positive eigenvalue. And it is responsible for the tumbling, the wild tumbling that you will see. And it's connected with the point staying on this hyperbola that wonders away from-- so it's this one now that I'm doing. This guy is the-- I'll put a box around-- a double box around it. That's the unstable one, which I'm about to demonstrate.
Ready? OK. Whoops. OK. It took two hands to catch it. Let me try it again. The point is it starts tumbling, and it goes in all directions. It's like a football, a really badly thrown football. It's like a football being thrown that goes end to end. The whole flight breaks up, and the ball is a mess. Catching it is ridiculous. And I'm doing it with a book. Yes. You saw that by watching really closely. OK. Better if you do it.
I'll end with the eigenvalues at this point. So the eigenvalues at that point-- can I just erase my matrix? So this was a neutrally stable one, a center in the language of stability. That's a center which you just go around and round and round. But now I'm going to just take x and z to be 0 and y to be 1. So can I erase that matrix and take--
If x and z are 0, and y is 1-- so I get a 1 down here. And I get a 1 up there. And nothing else. Everything else is 0. OK. That's my three by three matrix. What are its eigenvalues? What are the eigenvalues of that three by three very special matrix?
This is now the-- this was the first derivative matrix, the Jacobian matrix, at this point, corresponding to the middle axis. OK. Again, I'm seeing some 0s. I'll reduce this to that two by two matrix and this matrix. Really, I have this two by two matrix in the xz, and this one in the y. How about that guy?
You recognize what we're looking at with this matrix. So with that matrix, I can tell you the eigenvalues. We can see the trace is 0. The eigenvalues add to 0. They multiply to the determinant. And the determinant is minus 1. So the eigenvalues here are 1 and minus 1. And then this guy gives 0.
And it's that eigenvalue of 1 that's unstable. That eigenvalue of 1 is unstable. OK. So mathematics shows what the experiment shows: an unstable rotation tumbling around that middle axis. Thank you.