2 次元連続ウェーブレット変換

2 次元連続ウェーブレット変換 (CWT) は、膨張、回転、位置を表す 4 つの変数で 2 次元データ (イメージ データ) を表現します。膨張と回転は実数値のスカラーであり、位置は実数値の要素をもつ 2 次元ベクトルです。x を実数の 2 要素ベクトルとします。

$$f(x)\in L^2({ℝ}^2)$$

が平面上で二乗可積分である場合、2 次元 CWT は次のように定義されます。

$${\text{WT}}_f(a,b,\theta )={\displaystyle {\int }_{{ℝ}^2}f}(x)\frac{1}{a}\overline{\psi }\left(r_{-\theta }\left(\frac{x-b}{a}\right)\right)dx,a\in {ℝ}^{+},x,b\in {ℝ}^2,$$

ここで、バーは複素共役を表し、r_θ は次の 2 次元回転行列です。

$$r_{\theta }=\left(\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right),\theta \in [0,2\pi ).$$

2 次元 CWT は、イメージの空間スケール表現です。スケールの逆数と回転角度を合わせて空間周波数変数と見なすことができるため、2 次元 CWT は空間周波数表現であると解釈されます。

すべての 2 次元許容ウェーブレットにおいて、2 次元 CWT はスケールと位置に関してイメージのローカル フィルターとして機能します。ウェーブレットが等方性である場合、解析結果は角度に依存しません。メキシカン ハット ウェーブレット (リッカー ウェーブレットとも呼ばれる) は、等方性ウェーブレットの例です。等方性ウェーブレットは、イメージの点ごとの解析に適しています。ウェーブレットが異方性である場合、解析結果は角度に依存し、2 次元 CWT はスケール、位置、角度に関してイメージのローカル フィルターとして機能します。コーシー ウェーブレットは異方性ウェーブレットの例です。フーリエ領域では、これはウェーブレットの空間周波数サポートが原点に頂点をもつ凸円錐であることを意味します。異方性ウェーブレットは、イメージ内の方向に関する特徴を検出するのに適しています。

ウェーブレット イメージ アナライザー アプリを使用すると、イメージの連続ウェーブレット分解を可視化できます。このアプリを使用すると、分解結果をワークスペースにエクスポートしたり、結果を再現するためのスクリプトを生成したりすることができます。

等方性ウェーブレットと異方性ウェーブレットを使用したイメージの 2 次元 CWT の取得

イメージを読み込みます。

imdata = imread("triangle.jpg");
imagesc(imdata)

等方性ウェーブレット

等方性ウェーブレットを指定し、スケール 2、4、8、角度 0、$$\pi /6$$、$$\pi /3$$、$$\pi /2$$ におけるイメージの 2 次元 CWT を取得します。

wav = "mexh";
sca = [2 4 8];
rot = [0 1 2 3]*(pi/6);
imdata_CWT = cwtft2(imdata,Wavelet=wav,Scales=sca, ...
    Angles=rot);

すべてのスケールと角度における係数の大きさを表示します。補助関数 helperPlot2DCWT を使用します。このウェーブレットは等方性であるため、解析結果は角度に依存しません。等方性ウェーブレットは、イメージの点ごとの解析に適しています。

cfs = imdata_CWT.cfs;
figure(Position=[0 0 560 700])
helperPlot2DCWT(cfs,"Isotropic Wavelet")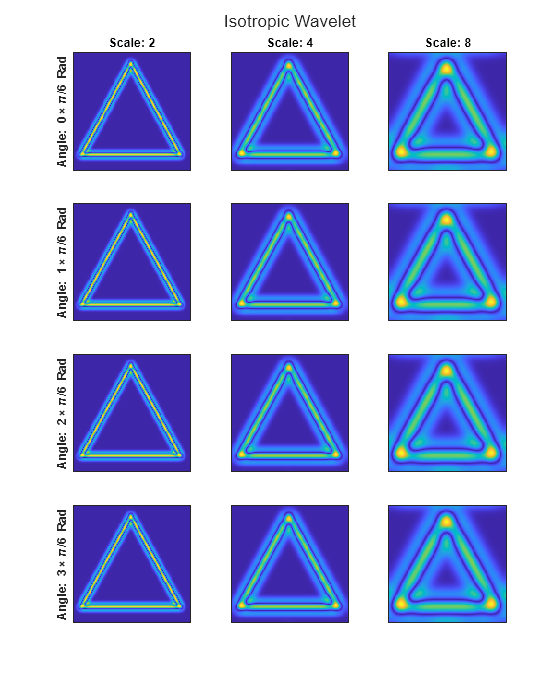

異方性ウェーブレット

同じスケールと角度でイメージの 2 次元 CWT を取得しますが、今回は異方性ウェーブレットを指定します。

wav = "morlet";
sca = [2 4 8];
rot = [0 1 2 3]*(pi/6);
imdata_CWT = cwtft2(imdata,Wavelet=wav,Scales=sca, ...
    Angles=rot);

すべてのスケールと角度における係数の大きさを表示します。このウェーブレットは異方性であるため、解析結果は角度に依存します。異方性ウェーブレットは、イメージ内の方向に関する特徴を検出するのに適しています。

cfs = imdata_CWT.cfs;
figure(Position=[0 0 560 700])
helperPlot2DCWT(cfs,"Anisotropic Wavelet")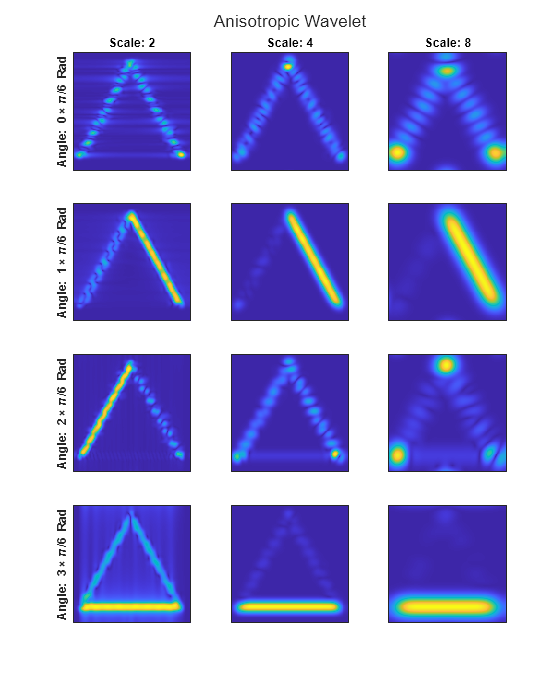

補助関数

function helperPlot2DCWT(cfs,str)
% This function is only intended to support this Wavelet example.
% It may change or be removed in a future release.
t=tiledlayout(4,3);
for i=1:4
    for j=1:3
        nexttile
        imagesc(abs(cfs(:,:,1,j,i)))
        if j==1
            ylabel("Angle: "+num2str(i-1)+"\times\pi/6 Rad", ...
                FontWeight="bold");
        end
        if i==1
            title("Scale: "+num2str(2^j));
        end
        xticks([])
        yticks([])
    end
end
title(t,str)
end

参考

アプリ

• ウェーブレット イメージ アナライザー

関数

• cwtft2 | cwtftinfo2

トピック

• Two-Dimensional CWT of Noisy Pattern
• Using Wavelet Image Analyzer App
• Viewing CWT Decomposition of Image in Wavelet Image Analyzer