大きくサンプリングされているウェーブレット パケット解析

この例では、1 次元信号のウェーブレット パケット変換を求める方法を示します。この例では、周波数順序が Paley 順序とは異なることも示します。

現在の境界拡大モードを保存し、モードを周期化に設定します。

st = dwtmode("status","nodisplay");
dwtmode("per","nodisp")

加法性ホワイト ガウス N(0,1/4) ノイズを伴う、周波数が $$7\pi /8$$ ラジアン/サンプルの正弦波を作成します。正弦波は、信号のサンプル 128 ～ 512 で発生します。

n = 0:1023;
indices = (n>127 & n<=512);
x = cos(7*pi/8*n).*indices+0.5*randn(size(n));

4 つの消失モーメントを持つ Daubechies 最小非対称ウェーブレットを使用し、レベル 2 まで下げてウェーブレット パケット変換を求めます。ウェーブレット パケット ツリーをプロットします。

T = wpdec(x,2,"sym4");
plot(T)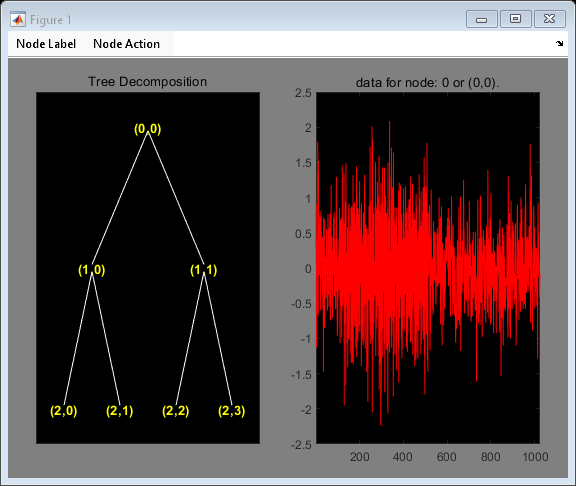

終端ノードの Paley および周波数順序を検出します。

[tn_pal,tn_freq] = otnodes(T)

tn_pal = 4×1

     3
     4
     5
     6

tn_freq = 4×1

     3
     4
     6
     5

tn_freq にはベクトル [3 4 6 5] が含まれています。これは、最も高い周波数範囲 $$[3\pi /4,\pi )$$ が実際には Paley 順序のウェーブレット パケット ツリーのノード 5 であることを示しています。

ウェーブレット パケット ツリーのノード (2,2) をクリックして、周波数順序が正弦波の存在を正しく予測していることを確認します。

2 次元イメージのウェーブレット パケット変換により、4 つの要素から成るウェーブレット パケット ツリーが得られます。イメージ例を読み込みます。再構成ウェーブレットに 3 つの消失モーメントと分解ウェーブレットに 5 つの消失モーメントを持つ双直交 B スプライン ウェーブレットを使用します。4 つの要素から成るウェーブレット パケット ツリーをプロットします。

load tartan
T = wpdec2(X,2,"bior3.5");
plot(T)

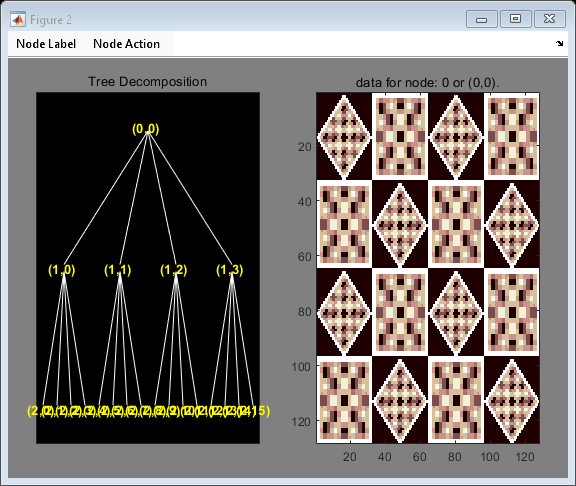
拡張モードを元に戻します。

dwtmode(st,"nodisplay")

参考

アプリ

• ウェーブレット信号アナライザー

関数

• dwpt | wavedec | wavedec2

トピック

• Practical Introduction to Multiresolution Analysis
• ウェーブレット パケット:Detail の分解