erfc

相補誤差関数

構文

erfc(X)

erfc(K,X)

説明

erfc(X) は、X の相補誤差関数である erfc(X) = 1 - erf(X) を表します。

erfc(K,X) は、X の相補誤差関数の累次積分である erfc(K, X) = int(erfc(K - 1, y), y, X, inf) を表します。

例

浮動小数点数およびシンボリック数の相補誤差関数

引数に応じて、erfc は浮動小数点解またはシンボリック厳密解の結果を返します。

次の数字について相補誤差関数を計算します。これらの数値はシンボリック オブジェクトではないため、結果は浮動小数点数となります。

A = [erfc(1/2), erfc(1.41), erfc(sqrt(2))]

A =
    0.4795    0.0461    0.0455

同じ数値をシンボリック オブジェクトに変換して相補誤差関数を計算します。ほとんどのシンボリックな (厳密な) 数値について、erfc は未解決のシンボリックな呼び出しを返します。

symA = [erfc(sym(1/2)), erfc(sym(1.41)), erfc(sqrt(sym(2)))]

symA =
[ erfc(1/2), erfc(141/100), erfc(2^(1/2))]

vpa を使用して、必要な桁数でシンボリックな結果を近似します。

d = digits(10);
vpa(symA)
digits(d)

ans =
[ 0.4795001222, 0.04614756064, 0.0455002639]

変数と式の誤差関数

ほとんどのシンボリックな変数と式では、erfc により未解決のシンボリックな呼び出しが返されます。

x および sin(x) + x*exp(x) について相補誤差関数を計算します。

syms x
f = sin(x) + x*exp(x);
erfc(x)
erfc(f)

ans =
erfc(x)
 
ans =
erfc(sin(x) + x*exp(x))

ベクトルと行列の相補誤差関数

入力引数がベクトルまたは行列である場合、erfc はそのベクトルまたは行列の要素ごとに相補誤差関数を返します。

行列 M とベクトル V の要素について相補誤差関数を計算します。

M = sym([0 inf; 1/3 -inf]);
V = sym([1; -i*inf]);
erfc(M)
erfc(V)

ans =
[         1, 0]
[ erfc(1/3), 2]
 
ans =
    erfc(1)
 1 + Inf*1i

V、M および整数 -1 の要素の相補誤差関数の累次積分を計算します。

erfc(-1, M)
erfc(-1, V)

ans =
[             2/pi^(1/2), 0]
[ (2*exp(-1/9))/pi^(1/2), 0]
 
ans =
 (2*exp(-1))/pi^(1/2)
                  Inf

相補誤差関数の特別な値

erfc は、特定のパラメーターの特別な値を返します。

x = 0、x = ∞、および x = –∞ について相補誤差関数を計算します。相補誤差関数にはこれらのパラメーター用の特別な値があります。

[erfc(0), erfc(Inf), erfc(-Inf)]

ans =
     1     0     2

複素数の無限大について相補誤差関数を計算します。sym を使用して複素数の無限大をシンボリック オブジェクトに変換します。

[erfc(sym(i*Inf)), erfc(sym(-i*Inf))]

ans =
[ 1 - Inf*1i, 1 + Inf*1i]

相補誤差関数を含む式の処理

diff や int など、多くの関数は erfc を含む式を処理することができます。

相補誤差関数の 1 次および 2 次導関数を計算します。

syms x
diff(erfc(x), x)
diff(erfc(x), x, 2)

ans =
-(2*exp(-x^2))/pi^(1/2)
 
ans =
(4*x*exp(-x^2))/pi^(1/2)

これらの式の積分を計算します。

syms x
int(erfc(-1, x), x)

ans =
erf(x)

int(erfc(x), x)

ans =
x*erfc(x) - exp(-x^2)/pi^(1/2)

int(erfc(2, x), x)

ans =
(x^3*erfc(x))/6 - exp(-x^2)/(6*pi^(1/2)) +...
(x*erfc(x))/4 - (x^2*exp(-x^2))/(6*pi^(1/2))

相補誤差関数のプロット

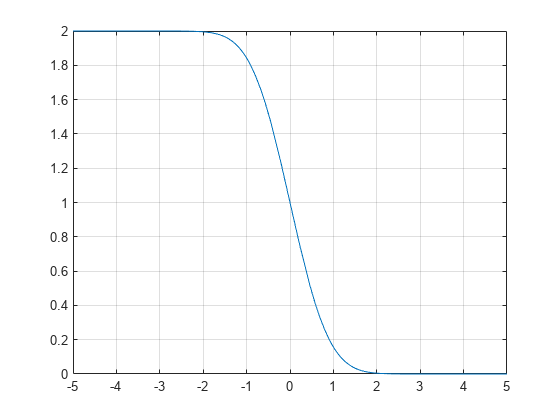
相補誤差関数を -5 から 5 までの範囲でプロットします。

syms x
fplot(erfc(x),[-5 5])
grid on

入力引数

X — 入力

シンボリック数 | シンボリック変数 | シンボリック式 | シンボリック関数 | シンボリック ベクトル | シンボリック行列

入力値。シンボリック数、変数、式または関数、あるいはシンボリック数、変数、式または関数のベクトルまたは行列として指定します。

K — -2 より大きい整数を表す入力

数値 | シンボリック数 | シンボリック変数 | シンボリック式 | シンボリック関数 | シンボリック ベクトル | シンボリック行列

入力は、数値、シンボリック数、変数、式または関数として指定された -2 より大きい整数を表します。この引数には、数値、シンボリック数、シンボリック変数、シンボリック式またはシンボリック関数のベクトルまたは行列を指定することもできます。

詳細

相補誤差関数

次の積分により相補誤差関数が定義されます。

$$erfc(x)=\frac{2}{\sqrt{\pi }}{\displaystyle \underset{x}{\overset{\infty }{\int }}{e}^{-t^2}dt}=1-erf\left(x\right)$$

ここで、erf(x) は誤差関数です。

相補誤差関数の累次積分

次の積分は相補誤差関数の累次積分です。

$$erfc\left(k,x\right)={\displaystyle \underset{x}{\overset{\infty }{\int }}erfc\left(k-1,y\right)dy}$$

ここでは、$$erfc\left(0,x\right)=erfc\left(x\right)$$ となります。

ヒント

• シンボリック オブジェクトではない数値について erfc を呼び出すと、MATLAB^® 関数 erfc が呼び出されます。この関数では実数の引数だけが受け入れられます。複素数の相補誤差関数を計算する場合は、sym を使用してその数値をシンボリック オブジェクトに変換し、そのシンボリック オブジェクトに対して erfc を呼び出します。

• ほとんどのシンボリックな (厳密な) 数値について、erfc は未解決のシンボリックな呼び出しを返します。vpa を使用して、結果を浮動小数点数で近似することができます。

• 少なくとも 1 つの入力引数はスカラーであるか、両方の引数は同じサイズのベクトルまたは行列でなければなりません。一方の入力引数がスカラーであり、もう一方の入力引数がベクトルまたは行列である場合、erfc によってスカラーは、すべての要素がそのスカラーと等しい、もう一方の引数と同じサイズのベクトルまたは行列に拡張されます。

アルゴリズム

ツールボックスを使用すれば、誤差関数とその逆関数を含む式を単純化できます。実数値 x については、ツールボックスは次の単純化ルールを適用します。

• erfinv(erf(x)) = erfinv(1 - erfc(x)) = erfcinv(1 - erf(x)) = erfcinv(erfc(x)) = x

• erfinv(-erf(x)) = erfinv(erfc(x) - 1) = erfcinv(1 + erf(x)) = erfcinv(2 - erfc(x)) = -x

任意の値 x については、系は次の単純化ルールを適用します。

• erfcinv(x) = erfinv(1 - x)

• erfinv(-x) = -erfinv(x)

• erfcinv(2 - x) = -erfcinv(x)

• erf(erfinv(x)) = erfc(erfcinv(x)) = x

• erf(erfcinv(x)) = erfc(erfinv(x)) = 1 - x

参照

[1] Gautschi, W. “Error Function and Fresnel Integrals.” Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (M. Abramowitz and I. A. Stegun, eds.). New York: Dover, 1972.

バージョン履歴

R2011b で導入

参考

erf | erfcinv | erfi | erfinv