ライブ エディター タスクを使用した代数方程式の求解
R2020a 以降、ライブ エディターで求解 (シンボリック式)タスクを使用して代数方程式を対話的に解き、シンボリック解を取得できます。ライブ エディター タスクの詳細については、ライブ スクリプトへの対話型タスクの追加を参照してください。
この例では次の解を求める方法を示します。
三角関数方程式
3 次方程式
連立 3 次方程式と連立線形方程式
三角関数方程式の求解
三角関数方程式 の解を、 と仮定して求めます。
まず、[ホーム] タブに移動し、![]() [新規ライブ スクリプト] をクリックしてライブ スクリプトを作成します。シンボリック変数
[新規ライブ スクリプト] をクリックしてライブ スクリプトを作成します。シンボリック変数 x を定義し、== 演算子を使用して三角関数方程式の等号を表します。assume を使用して x に仮定を設定します。
syms x
eqn = sin(x) + cos(x) == 0;
assume(x > pi/2);[ライブ エディター] タブで、![]() [実行] をクリックしてコードを実行し、
[実行] をクリックしてコードを実行し、x とその仮定および eqn を現在のワークスペースに保存します。
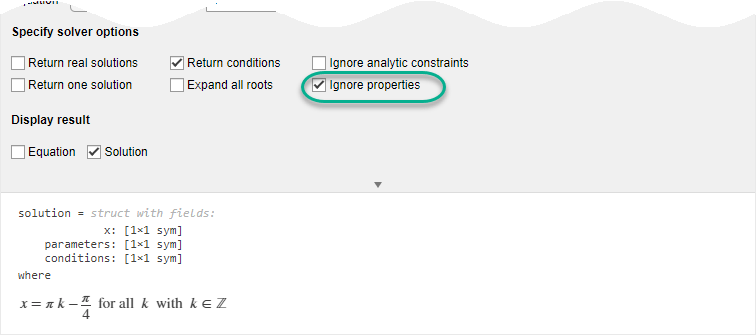
次に、[ライブ エディター] タブで [タスク]、[求解 (シンボリック式)] を選択して、[求解 (シンボリック式)] タスクを開きます。三角関数方程式の解を求めるには、ワークスペースからシンボリック方程式 eqn を選択します。解を求める変数として x を指定します。[条件を返す] オプションを選択すると、一般的な解とそれが保持する解析制約を返します。

[プロパティを無視] オプションを選択すると、x の仮定を無視できます。 という仮定を使用せずに解を返します。
シンボリック方程式の求解を試すには、他のシステム方程式やソルバー オプションについても上記の手順を繰り返すことができます。以下の例は、既存のライブ スクリプトにコードを追加するか新規ライブ スクリプトを作成して実行できます。
3 次方程式の求解
3 次方程式 の解を求めます。
syms を使用してシンボリック変数 x および y を定義し、== 演算子を使用して 3 次方程式の等号を表します。
syms x y cubicEquation = x^3 - 2*x^2 + y == 0;
3 次方程式の解を求めるには、ワークスペースからシンボリック方程式 cubicEquation を選択します。解を求める変数として x を指定します。
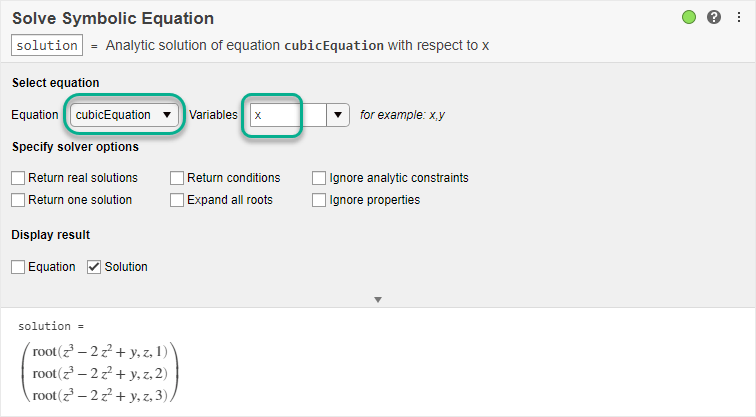
ソルバーは関数 root でシンボリック解を返します。関数 root を平方根で表現するには、[すべてのルートを展開] オプションを選択します。
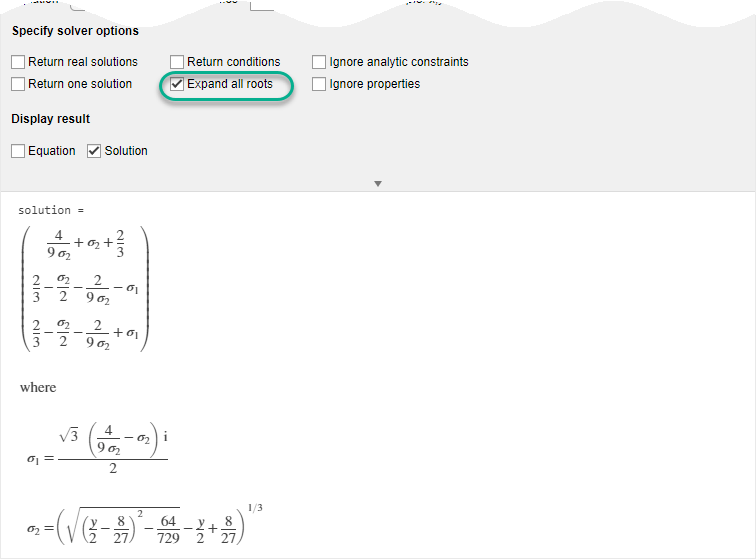
連立方程式の求解
次の連立 3 次方程式と連立線形方程式の解を求めます。
syms を使用してシンボリック変数 x および y を定義します。== 演算子を使用して方程式の等号を表します。連立方程式を宣言するには、2 つのシンボリック方程式を配列に組み合わせます。
syms x y cubicEquation = x^3 - 2*x^2 + y == 0; linearEquation = y == 4*x - 8; systemEquations = [cubicEquation linearEquation];
連立方程式の解を求めるには、ワークスペースからシンボリック方程式 systemEquations を選択します。解を求める変数として x と y を指定します。

ソルバーは実数解と複素数解を返します。実数解のみを表示するには、[実数解を返す] オプションを選択します。
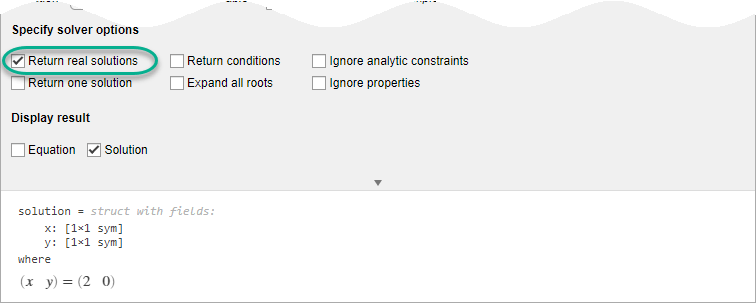
コードの生成
タスクが使用したコードを表示するには、タスク ウィンドウ下部の ![]() をクリックします。タスクにコード ブロックが表示されます。これをコピーして貼り付けることで、後で既存のスクリプトや別のプログラムで使用したり変更したりできます。以下に例を示します。
をクリックします。タスクにコード ブロックが表示されます。これをコピーして貼り付けることで、後で既存のスクリプトや別のプログラムで使用したり変更したりできます。以下に例を示します。
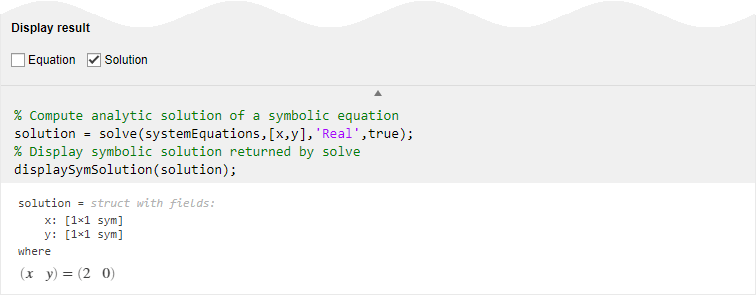
基となるコードがライブ スクリプトの一部になっているため、タスクによって生成された解を使用して、さらに処理を継続できます。たとえば、連立方程式とその実数解をプロットできます。
