多変量回帰の問題の設定

応答行列

mvregress を使用して多変量線形回帰モデルの当てはめを行うには、応答行列と計画行列を特定の方法で設定しなければなりません。正しい形式の入力を指定すると、mvregress ではさまざまな多変量回帰の問題に対処できます。

mvregress は、潜在的に相関する d 次元の応答の n 観測値は、Y などの名前の n 行 d 列の行列になると予測します。つまり、依存関係構造が同じ "行" 内の観測値間に存在するように応答を設定します。Y を長さのベクトル n (行ベクトルまたは列ベクトル) として指定した場合、mvregress は、d = 1 と仮定し、要素を n 個の独立な観測として処理します。ベクトルは相関系列 (時系列など) の 1 つの実現として "モデル化されません"。

応答行列の設定方法の例として、多変量応答が、次の図に示すように複数の時点で被験者に対して繰り返し行われる測定であるとします。

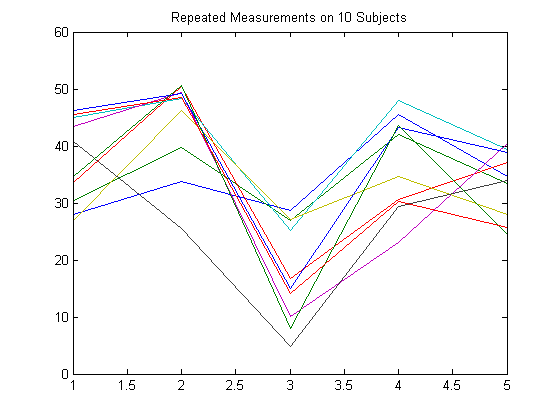
Plot of repeated measurements, where each line corresponds to one subject. The x-axis shows the time points at which the measurements are made.

1 人の被験者内の観測は相関するものとします。

Plot of repeated measurements, where the dark blue points indicate within subject correlation

この例では、応答行列 Y を、各行が 1 人の被験者を表し、各列が 1 つの時点を表すよう設定します。

Response matrix with subjects in rows and time points in columns

ここでも、同時に被験者に行われた観測は相関する (同時相関) ものとします。

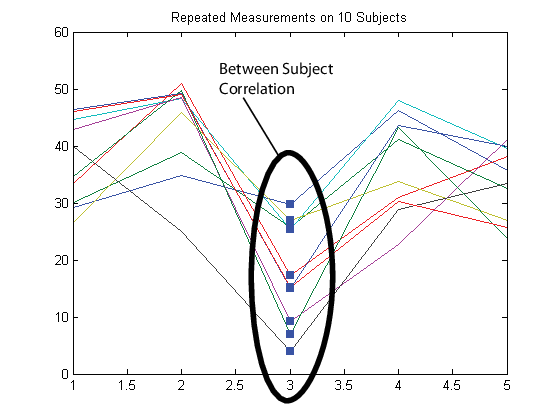
Plot of repeated measurements, where the dark blue points indicate between subject correlation

この例では、応答行列 Y を、各行が 1 つの時点を表し、各列が 1 人の被験者を表すよう設定します。

Response matrix with time points in rows and subjects in columns

計画行列

多変量線形回帰モデルでは、d 次元の応答ごとに対応する計画行列があります。モデルによっては、計画行列に外因的予測子変数、ダミー変数、ラグ応答、またはこれらとその他の共変量項を組み合わせて構成される場合があります。

d > 1 であり、すべての d 次元で同じ計画行列をもつ場合は、n 行 p 列の計画行列を 1 つ指定します (p は予測子変数の数)。各次元の切片を決定するには、1 の列を計画行列に追加します。この場合、mvregress は計画行列をすべての d 次元に適用します。
d > 1 であり d 次元に同じ計画行列をもたないものがある場合は、d 行 K 列の配列から成る長さ n の cell 配列 (たとえばX という名前) を使用して計画行列を指定します。K はモデル内の回帰係数の総数です。X 内の配列の行は、応答行列 Y の列に対応することに注意してください。

n 回のすべての観測が同じ計画行列をもつ場合、1 つの d 行 K 列の計画行列を含む cell 配列を指定できます。この例では、mvregress は計画行列を n 回のすべての観測に適用します。たとえば、予測子が時間の関数であるときに、すべての観測が同じ時点で測定された場合に、この状況になる可能性があります。
d = 1 となる特殊なケースでは、1 つの n 行 K 列の計画行列 (cell 配列内に含まれていない) を指定できます。ただし、fitlm を使用して回帰モデルを一変量の連続応答に当てはめることを検討する必要があります。

以下の節では、mvregress を使用して推定の一般的な多変量回帰の問題を設定する方法を示します。

多変量一般線形モデル

多変量一般線形モデルは、次の形式になります。

$Y_{n \times d} = X_{n \times (p + 1)} B_{(p + 1) \times d} + E_{n \times d} .$

展開された形式は次のとおりです。

$[\begin{array}{l} y_{11} y_{12} \dots y_{1 d} \\ y_{21} y_{22} \dots y_{2 d} \\ ⋮ ⋮ ⋱ ⋮ \\ y_{n 1} y_{n 2} \dots y_{n d} \end{array}] = [\begin{array}{l} 1 x_{11} x_{12} \dots x_{1 p} \\ 1 x_{21} x_{22} \dots x_{2 p} \\ ⋮ ⋮ ⋮ ⋱ ⋮ \\ 1 x_{n 1} x_{n 2} \dots x_{n p} \end{array}] [\begin{array}{l} β_{01} β_{02} \dots β_{0 d} \\ β_{11} β_{12} \dots β_{1 d} \\ ⋮ ⋮ ⋱ ⋮ \\ β_{p 1} β_{p 2} \dots β_{p d} \end{array}] + [\begin{array}{l} ε_{11} ε_{12} \dots ε_{1 d} \\ ε_{21} ε_{22} \dots ε_{2 d} \\ ⋮ ⋮ ⋱ ⋮ \\ ε_{n 1} ε_{n 2} \dots ε_{n d} \end{array}] .$

つまり、各 d 次元の応答には切片と p 個の予測子変数が、各次元には別々の回帰係数のセットが含まれています。この形式では、最小二乗解は B = X\Y です。mvregress を使用してこのモデルを推定するには、上記のように、応答の n 行 d 列の行列を使用します。

すべての d 次元が同じ計画行列をもつ場合は、上記のように n 行 (p+1) 列の計画行列を使用します。p 個の予測子変数に 1 の列を追加すると、各次元の切片が計算されます。

d 次元に同じ計画行列をもたないものがある場合は、n 行 (p + 1) 列の計画行列を、d 行 K 列の行列から成る長さ n の cell 配列に再構成します。ここで各次元の切片と傾きに対して K = (p + 1)d です。

たとえば、n = 4、d = 3、p = 2 (1 つの切片に加えて 2 つの予測子項) であるとします。次の図は、cell 配列内の i 番目の要素を構成する方法を示しています。

$[\begin{matrix} y_{11} & y_{12} & y_{13} \\ \begin{matrix} y_{21} \\ y_{31} \end{matrix} & \begin{matrix} y_{22} \\ y_{32} \end{matrix} & \begin{matrix} y_{23} \\ y_{33} \end{matrix} \\ y_{41} & y_{42} & y_{43} \end{matrix}] = \underset{\begin{matrix} ↓ \\ \underset{X {i}}{\underset{︸}{[\begin{matrix} \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} & \begin{matrix} x_{i 1} & 0 & 0 \\ 0 & x_{i 1} & 0 \\ 0 & 0 & x_{i 1} \end{matrix} & \begin{matrix} x_{i 2} & 0 & 0 \\ 0 & x_{i 2} & 0 \\ 0 & 0 & x_{i 2} \end{matrix} \end{matrix}]}} [\begin{matrix} β_{01} \\ β_{02} \\ β_{03} \\ \begin{matrix} \begin{matrix} β_{11} \\ β_{12} \\ β_{13} \end{matrix} \\ β_{21} \\ β_{22} \\ β_{23} \end{matrix} \end{matrix}] \end{matrix}}{\underset{︸}{[\begin{matrix} 1 & x_{11} & x_{12} \\ \begin{matrix} 1 \\ 1 \end{matrix} & \begin{matrix} x_{21} \\ x_{31} \end{matrix} & \begin{matrix} x_{22} \\ x_{32} \end{matrix} \\ 1 & x_{41} & x_{42} \end{matrix}] [\begin{matrix} β_{01} & β_{02} & β_{03} \\ β_{11} & β_{12} & β_{13} \\ β_{21} & β_{22} & β_{23} \end{matrix}]}} + [\begin{matrix} ε_{11} & ε_{12} & ε_{13} \\ \begin{matrix} ε_{21} \\ ε_{31} \end{matrix} & \begin{matrix} ε_{22} \\ ε_{32} \end{matrix} & \begin{matrix} ε_{23} \\ ε_{33} \end{matrix} \\ ε_{41} & ε_{42} & ε_{43} \end{matrix}]$

必要に応じて、推定後に、係数の K 行 1 列のベクトルを (p + 1) 行 d 列の行列の形状に戻すことができます。

モデルパラメーターに制約を付けるには、それに合わせて計画行列を調整します。たとえば、前の例の 3 つの次元に 1 つの共通する傾きがあるとします。つまり、 $β_{11} = β_{12} = β_{13} = β_{1}$ および $β_{21} = β_{22} = β_{23} = β_{2} .$ とします。この場合、次の図に示すように各計画行列は 3 行 5 列になります。

$\underset{X {i}}{\underset{︸}{[\begin{matrix} \begin{matrix} 1 & 0 & 0 \end{matrix} & x_{i 1} & x_{i 2} \\ \begin{matrix} 0 & 1 & 0 \end{matrix} & x_{i 1} & x_{i 2} \\ \begin{matrix} 0 & 0 & 1 \end{matrix} & x_{i 1} & x_{i 2} \end{matrix}]}} [\begin{matrix} \begin{matrix} β_{01} \\ β_{02} \end{matrix} \\ β_{03} \\ β_{1} \\ β_{2} \end{matrix}]$

縦方向解析

縦方向解析では、同一の被験者に行われた観測間の相関によって、d 時点の n 人の被験者の応答を測定する場合があります。たとえば、t_ij、i = 1,...,n および j = 1,...,d 時点の応答 y_ij を測定するとします。また、各被験者が、指標変数 G_i で指定された 2 つのグループの一方 (男性または女性など) に含まれるとします。グループ固有の切片と傾きを使用すると、次のように G_i および t_ij の関数として y_ij をモデル化できます。

$y_{i j} = β_{0} + β_{1} G_{i} + β_{2} t_{i j} + β_{3} G_{i} \times t_{i j} + ε_{i j}, i = 1, \dots, n; j = 1, \dots, d,$

ここで

$ε_{i} = (ε_{i 1}, \dots, ε_{i d})^{'} \sim M V N (0, Σ) .$

ほとんどの縦方向モデルには、明示的予測子として時間が含まれます。

mvregress を使用してこのモデルを当てはめるには、n 行 d 列の行列の応答を調整します。n は被験者の数で、d は時間点の数です。d 行 K 列の行列の n 長の cell 配列で計画行列を指定します。ここで、K = 4 は 4 つの回帰係数を表します。

たとえば、d = 5 (被験者あたり 5 回の観測) とします。指定されたモデルの i 番目の計画行列と対応するパラメーターベクトルを次の図に示します。

$\underset{X {i}}{\underset{︸}{[\begin{matrix} 1 & G_{i} & t_{i 1} & G_{i} \times t_{i 1} \\ 1 & G_{i} & t_{i 2} & G_{i} \times t_{i 2} \\ 1 & G_{i} & t_{i 3} & G_{i} \times t_{i 3} \\ \begin{matrix} 1 \\ 1 \end{matrix} & \begin{matrix} G_{i} \\ G_{i} \end{matrix} & \begin{matrix} t_{i 4} \\ t_{i 5} \end{matrix} & \begin{matrix} G_{i} \times t_{i 4} \\ G_{i} \times t_{i 5} \end{matrix} \end{matrix}]}} [\begin{matrix} β_{0} \\ β_{1} \\ β_{2} \\ β_{3} \end{matrix}]$

パネル解析

パネル解析では、d 被験者 (個人または国など) について、n 時間点における応答と共変量を測定する場合もあります。たとえば、t = 1,...,n 時点における被験者 j = 1,...,d に対する応答 y_tj および共変量 x_tj を測定するとします。被験者固有の固定効果が含まれている固定効果のパネルモデルと同時相関は次のようになります。

$y_{t j} = α_{j} + β x_{t j} + ε_{t j},$

ここで

$ε_{t} = (ε_{t 1}, ..., ε_{t d})^{'} \sim M V N (0, Σ) .$

縦方向モデルでは時間を明示的な予測子として使用しますが、一般にパネル解析モデルには各時間点で測定した共変量が含まれます。

mvregress を使用してこのモデルを当てはめるには、n 行 d 列の行列の応答を調整して、各列が 1 人の被験者に対応するようにします。d 行 K 列の行列の n 長の cell 配列で計画行列を指定します。ここで、K = d + 1 は d の切片と傾き項を表します。

たとえば、d = 4 (4 人の被験者) とします。t 番目の計画行列と対応するパラメーターベクトルを次の図に示します。

$\underset{X {t}}{\underset{︸}{[\begin{matrix} 1 & 0 & 0 & \begin{matrix} 0 & x_{t 1} \end{matrix} \\ 0 & 1 & 0 & \begin{matrix} 0 & x_{t 2} \end{matrix} \\ 0 & 0 & 1 & \begin{matrix} 0 & x_{t 3} \end{matrix} \\ 0 & 0 & 0 & \begin{matrix} 1 & x_{t 4} \end{matrix} \end{matrix}]}} [\begin{matrix} \begin{matrix} α_{1} \\ α_{2} \end{matrix} \\ α_{3} \\ α_{4} \\ β \end{matrix}]$

見かけ上無関係な回帰

見かけ上無関係な回帰 (SUR) では、切片と傾きがそれぞれ独自であり、誤差の分散共分散行列が共通している d 個の独立した回帰をモデル化します。たとえば、回帰モデル j = 1,...,d の応答 y_ij と共変量 x_ij を、i = 1,...,n 観測を使用して測定し、各回帰を近似するとします。SUR モデルは次のようになります。

$y_{i j} = β_{0 j} + β_{j} x_{i j} + ε_{i j},$

ここで

$ε_{i} = (ε_{i 1}, \dots, ε_{i d})^{'} \sim M V N (0, Σ) .$

このモデルは、各次元の共変量が異なる点を除き、多変量一般線形モデルに似ています。

mvregress を使用してこのモデルを当てはめるには、n 行 d 列の行列の応答を調整して、各列に j 番目の回帰モデルのデータが含まれるようにします。d 行 K 列の行列の n 長の cell 配列で計画行列を指定します。ここで、K = 2d は d 個の切片と d 個の傾きを表します。

たとえば、d = 3 (3 つの回帰) とします。i 番目の計画行列と対応するパラメーターベクトルを次の図に示します。

$\underset{X {i}}{\underset{︸}{[\begin{matrix} \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} & \begin{matrix} x_{i 1} & 0 & 0 \\ 0 & x_{i 2} & 0 \\ 0 & 0 & x_{i 3} \end{matrix} \end{matrix}]}} [\begin{matrix} \begin{matrix} β_{01} \\ β_{02} \end{matrix} \\ β_{03} \\ β_{1} \\ \begin{matrix} β_{2} \\ β_{3} \end{matrix} \end{matrix}]$

ベクトル自己回帰モデル

VAR(p) ベクトル自己回帰モデルでは、d 次元の時系列応答を、前の時間からの p のラグ d 次元応答の線形関数として表します。たとえば、t = 1,...,n 時点における時系列 j = 1,...,d の応答 y_tj を測定するとします。VAR(p) モデルは次のようになります。

$[\begin{array}{l} y_{t 1} \\ y_{t 2} \\ ⋮ \\ y_{t d} \end{array}] = [\begin{array}{l} c_{1} \\ c_{2} \\ ⋮ \\ c_{d} \end{array}] + [\begin{array}{l} φ_{11}^{(1)} φ_{12}^{(1)} \dots φ_{1 d}^{(1)} \\ ⋮ ⋮ ⋱ ⋮ \\ φ_{d 1}^{(1)} φ_{d 2}^{(1)} \dots φ_{d d}^{(1)} \end{array}] [\begin{array}{l} y_{t - 1, 1} \\ y_{t - 1, 2} \\ ⋮ \\ y_{t - 1, d} \end{array}] + \dots + [\begin{array}{l} φ_{11}^{(p)} φ_{12}^{(p)} \dots φ_{1 d}^{(p)} \\ ⋮ ⋮ ⋱ ⋮ \\ φ_{d 1}^{(p)} φ_{d 2}^{(p)} \dots φ_{d d}^{(p)} \end{array}] [\begin{array}{l} y_{t - p, 1} \\ y_{t - p, 2} \\ ⋮ \\ y_{t - p, d} \end{array}] + [\begin{array}{l} ε_{t 1} \\ ε_{t 2} \\ ⋮ \\ ε_{t d} \end{array}],$

ここで

$ε_{t} = (ε_{t 1}, ..., ε_{t d})^{'} \sim M V N (0, Σ) .$

一般に、ベクトル自己回帰モデルを推定する場合は、最初の p 観測値を使用してモデルを開始するか、他の事前標本応答値を用意する必要があります。

mvregress を使用してこのモデルを当てはめるには、n 行 d 列の行列の応答を調整して、各列が 1 つの時系列に対応するようにします。d 行 K 列の行列の n 長の cell 配列で計画行列を指定します。ここでは、K = d + pd² となります。

たとえば、d = 2 (2 つの時系列) および p = 1 (1 ラグ) とします。t 番目の計画行列と対応するパラメーターベクトルを次の図に示します。

$\underset{X {t}}{\underset{︸}{[\begin{matrix} \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} & \begin{matrix} y_{t - 1, 1} & 0 \\ 0 & y_{t - 1, 1} \end{matrix} & \begin{matrix} y_{t - 1, 2} & 0 \\ 0 & y_{t - 1, 2} \end{matrix} \end{matrix}]}} [\begin{matrix} \begin{matrix} c_{1} \\ c_{2} \end{matrix} \\ φ_{11}^{(1)} \\ φ_{21}^{(1)} \\ \begin{matrix} φ_{12}^{(1)} \\ φ_{22}^{(1)} \end{matrix} \end{matrix}]$

また、Econometrics Toolbox™ には VAR(p) モデルの当てはめと予測のための関数があり、外因的予測子変数を指定するオプションもあります。

参考

mvregress | mvregresslike