縦方向解析
この例では、mvregress を使用して縦方向解析を実行する方法を示します。
標本データを読み込みます。
標本の縦方向データを読み込みます。
load longitudinalData行列 Y には 16 人の応答データが含まれています。応答は 5 つの時間点 (t = 0、2、4、6、8) で測定された薬の血中濃度です。Y の各行は 1 人の個人に対応し、各列は 1 つの時間点に対応します。最初の 8 人の被験者は女性で、次の 8 人の被験者は男性です。このデータは、シミュレーションされたものです。
データをプロットする。
16 人の被験者すべてのデータをプロットします。
figure() t = [0,2,4,6,8]; plot(t,Y) hold on hf = plot(t,Y(1:8,:),'^'); hm = plot(t,Y(9:16,:),'o'); legend([hf(1),hm(1)],'Female','Male','Location','NorthEast') title('Longitudinal Response') ylabel('Blood Drug Level') xlabel('Time') hold off

計画行列を定義する。
yij で、tij、j = 1,...,d の時点で測定された個人の i = 1,...,n の応答を示します。この例では、n = 16 および d = 5 になります。Gi で個人 i の性別を表し、男性の場合は Gi = 1、女性の場合は 0 とします。
性別ごとに傾きと切片が異なる、二次縦方向モデルの当てはめを考えます。
ここで、 です。誤差相関では、個人内でのクラスタリングが考慮されます。
mvregress を使用してこのモデルを当てはめるには、応答データが n 行 d 列の行列に含まれている必要があります。Y は既に適切な形式になっています。
次に、d 行 K 列の計画行列の長さが n の cell 配列を作成します。このモデルの場合は、K = 6 個のパラメーターがあります。
個人 i について、5 行 6 列の計画行列は次のようになります。
これは、次のパラメーター ベクトルに対応します。
行列 X1 には女性についての計画行列、X2 には男性についての計画行列が含まれています。
計画行列の cell 配列を作成します。最初の 8 人は女性で、次の 8 人は男性です。
X = cell(8,1);
X(1:8) = {X1};
X(9:16) = {X2};
モデルを当てはめる。
最尤推定法を使用してモデルを当てはめます。推定係数と標準誤差を表示します。
[b,sig,E,V,loglikF] = mvregress(X,Y); [b sqrt(diag(V))]
ans =
18.8619 0.7432
13.0942 1.0511
2.5968 0.2845
-0.3771 0.0398
-0.5929 0.4023
0.0290 0.0563交互作用項 (b の最後の 2 行) の係数は重要には見えません。この近似に対数尤度目的関数の値 loglikF を使用すると、このモデルを尤度比検定を使用して交互作用項のないモデルと比較できます。
近似したモデルをプロットする。
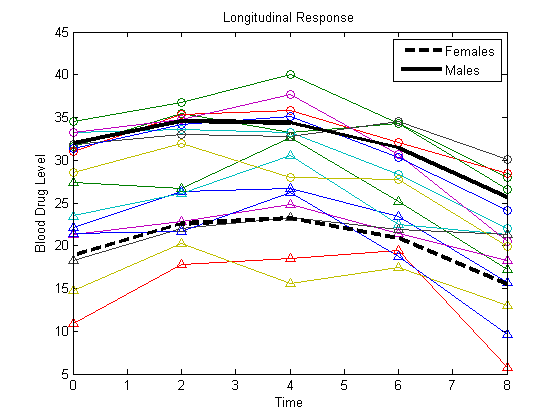
女性と男性の近似の直線をプロットします。
Yhatf = X1*b; Yhatm = X2*b; figure() plot(t,Y) hold on plot(t,Y(1:8,:),'^',t,Y(9:16,:),'o') hf = plot(t,Yhatf,'k--','LineWidth',3); hm = plot(t,Yhatm,'k','LineWidth',3); legend([hf,hm],'Females','Males','Location','NorthEast') title('Longitudinal Response') ylabel('Blood Drug Level') xlabel('Time') hold off
次元削減されたモデルを定義する。
交互作用項がないモデルを当てはめます。
ここで、 です。
このモデルには 4 つの係数があり、計画行列 X1 および X2 (それぞれ女性用および男性用) の最初の 4 列に対応しています。
X1R = X1(:,1:4);
X2R = X2(:,1:4);
XR = cell(8,1);
XR(1:8) = {X1R};
XR(9:16) = {X2R};
次元削減されたモデルを当てはめる。
最尤推定法を使用してこのモデルを当てはめます。推定係数とそれらの標準誤差を表示します。
[bR,sigR,ER,VR,loglikR] = mvregress(XR,Y); [bR,sqrt(diag(VR))]
ans =
19.3765 0.6898
12.0936 0.8591
2.2919 0.2139
-0.3623 0.0283尤度比検定を実行する。
尤度比検定を使用して 2 つのモデルを比較します。帰無仮説は、次元削減されたモデルが十分であるということです。対立仮説は、次元削減されたモデルが (交互作用項をもつ完全なモデルと比較して) 不適切であるとします。
尤度比検定統計は、2 つの自由度をもつ (2 つの係数が脱落している場合) カイ二乗分布と比較されます。
LR = 2*(loglikF-loglikR); pval = 1 - chi2cdf(LR,2)
pval =
0.08030.0803 は、有意水準 5% で帰無仮説が棄却されていないことを示します。したがって、項数の追加によって近似が向上するという十分な証拠はありません。