応答曲面計画
応答曲面計画の紹介
2 次応答曲面は、応答の形について追加の仮定をせずに、最大または最小を与える簡単なモデルです。2 次モデルは、各因子が 3 水準以上の完全実施要因計画を使ってキャリブレートできますが、これらの計画は一般的に、モデル パラメーターの正確な推定に必要以上の実行回数を伴います。この節では、各因子の 3 または 5 水準を使用して (ただし、水準の組み合わせのすべては使用せずに)、水準の組み合わせをすべて使用せずに、2 次モデルをより効率的にキャリブレートする計画を説明します。
中心複合計画
中心複合計画 (CCD) は、Box-Wilson 計画としても知られ、完全 2 次モデルのキャリブレーションに適します。以下に図示する、3 種類の CCD (circumscribed、inscribed、faced) があります。
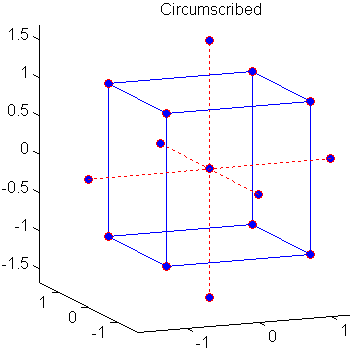
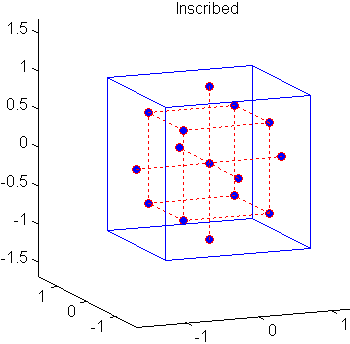

各計画は、要因計画 (立方体の頂点) と 2 次の効果の推定が可能な、center と star 点とで構成されます。n 個の因子をもつ完全 2 次モデルの場合、CCD は (n+2)(n+1)/2 個の係数を推定するのに十分な計画点を持ちます。
使用される CCD のタイプ (因子の点と star 点の位置) は、要因の数と、目的とする計画の特性で決められます。次の表に、いくつかの重要な特性をまとめてあります。予測の分散が計画の中心から計画点までの距離のみに依存する場合、計画は "回転可能" です。
| 設計 | 回転可能 | 因子水準 | ±1 の外の点の利用 | 推定の精度 |
|---|---|---|---|---|
| Circumscribed (CCC) | あり | 5 | あり | 計画空間全体に対し適切 |
| Inscribed (CCI) | あり | 5 | なし | 計画空間の中心サブセットに対し適切 |
| Faced (CCF) | なし | 3 | なし | 計画空間全体に対し適切。pure 2 次係数に対し不適切 |
関数 ccdesign を使って、CCD を作成します。
dCC = ccdesign(3,"Type","circumscribed")
dCC =
-1.0000 -1.0000 -1.0000
-1.0000 -1.0000 1.0000
-1.0000 1.0000 -1.0000
-1.0000 1.0000 1.0000
1.0000 -1.0000 -1.0000
1.0000 -1.0000 1.0000
1.0000 1.0000 -1.0000
1.0000 1.0000 1.0000
-1.6818 0 0
1.6818 0 0
0 -1.6818 0
0 1.6818 0
0 0 -1.6818
0 0 1.6818
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0繰り返された中心点の実行は、計画空間全体での予測の分散のより一様な推定を可能にします。
ボックスベーンケン計画
中心複合計画で説明した計画のように、ボックスベーンケン計画は、完全 2 次モデルに近似するために使用されます。ボックスベーンケン計画は回転ができ、少数 (4 以下) の要因に対して、CCD よりも実行が少なくて済みます。計画空間の角点を避けることによって、実験者が極端な因子の組み合わせに対処できます。しかし、inscribed CCD のように、extremes の推定は不適切になります。
ボックスベーンケン計画の配置は、次の図に示します。
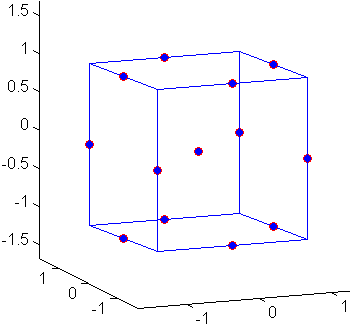
計画点は、計画空間の中心点と辺の中点にあり、組み込まれた要因計画を含みません。
関数 bbdesign を使って、ボックスベーンケン計画を作成します。
dBB = bbdesign(3)
dBB =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0ここでも、繰り返された中心点の実行によって、計画空間全体についての予測分散のより一様な推定ができます。