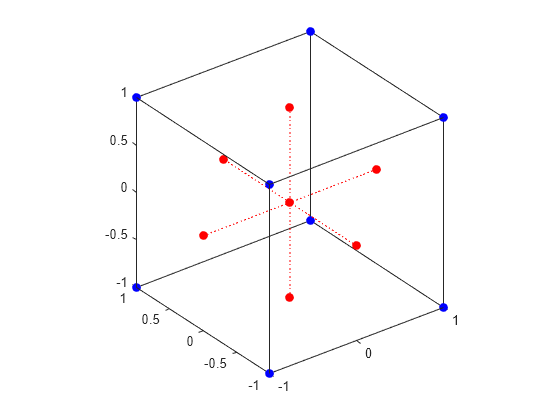
ccdesign

中心複合計画

ページ内をすべて折りたたむ

構文

dCC = ccdesign(n)
dCC = ccdesign(n,Name=Value)
[dCC,blocks] = ccdesign(___)

説明

dCC = ccdesign(n) は、n 因子の中心複合 (Box-Wilson) 計画を含む数値行列 dCC を返します。ここで、n は範囲 [2, 26] の正の整数スカラーです。dCC のサイズは m 行 n 列です。ここで、m は計画の実行回数 (点数) です。dCC の各行には、その実行のすべての因子の設定が含まれます。因子の値は、キューブ ポイントが –1 と 1 の間の値を取るように正規化されます。

例

dCC = ccdesign(n,Name=Value) は、1 つ以上の名前と値の引数で指定された追加オプションを使用して dCC を返します。たとえば、中心点の数やブロックあたりの最大点数を指定できます。

例

[dCC,blocks] = ccdesign(___) は、前の構文におけるいずれかの入力引数の組み合わせを使用して、実行ごとのブロック番号を含む 1 行 m 列のベクトルを追加で返します。ブロックは、パラメーター推定においてブロック間の差の影響を最小にするために同様の条件で測定される実行のことを指します。

例

例

すべて折りたたむ

ライブ スクリプトを開く

2 要素の中心複合外接計画を作成します。

dCC = ccdesign(2);

計画の最後の 10 個の実行を表示します。

disp(dCC(end-9:end,:))
         0   -1.4142
         0    1.4142
         0         0
         0         0
         0         0
         0         0
         0         0
         0         0
         0         0
         0         0

この計画には 8 つの中心点が含まれ、推定した係数間での相関を減らします。

設計を可視化します。

plot(dCC(:,1),dCC(:,2),"ro",MarkerFaceColor="b")
X = [1 -1 -1 -1; 1 1 1 -1];
Y = [-1 -1 1 -1; 1 -1 1 1];
line(X,Y,Color="b")
axis square equal

Figure contains an axes object. The axes object contains 5 objects of type line. One or more of the lines displays its values using only markers

各点の座標は、計画における実行の要因設定を表します。外接計画では、4 つの点がメインの正方形の外部に配置されます。

ライブ スクリプトを開く

面接タイプの 3 要素の中心複合計画を作成します。

[dCC,blocks] = ccdesign(3,Type="faced")
dCC = 24×3

    -1    -1    -1
    -1    -1     1
    -1     1    -1
    -1     1     1
     1    -1    -1
     1    -1     1
     1     1    -1
     1     1     1
    -1     0     0
     1     0     0
     0    -1     0
     0     1     0
     0     0    -1
     0     0     1
     0     0     0
      ⋮


blocks = 24×1

     1
     1
     1
     1
     1
     1
     1
     1
     2
     2
     2
     2
     2
     2
     1
      ⋮

設計を可視化します。最初のブロックの実行を青色の点で表示し、2 番目のブロックの実行を赤色の点で表示します。

plot3(dCC(blocks == 1,1),dCC(blocks==1,2),dCC(blocks==1,3),"bo", ...
         MarkerFaceColor="b")
hold on
plot3(dCC(blocks == 2,1),dCC(blocks==2,2),dCC(blocks==2,3),"ro", ...
         MarkerFaceColor="r")
set(gca,Box="on",BoxStyle="full")
line([0 0],[0,0],[-1 1],Color="r",LineStyle=":")
line([-1 1],[0,0],[0 0],Color="r",LineStyle=":")
line([0 0],[-1,1],[0 0],Color="r",LineStyle=":")
axis square equal
hold off

Figure contains an axes object. The axes object contains 5 objects of type line. One or more of the lines displays its values using only markers

各点の座標は、計画における実行の要因設定を表します。この計画は面接タイプであるため、各スター点はキューブの面に配置されます。

入力引数

すべて折りたたむ

計画の因子数。範囲 [2,26] の整数スカラーとして指定します。

例: 3

データ型: single | double

名前と値の引数

すべて折りたたむ

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: ccdesign(3,Center=2) は、2 つの中心点を含む 3 因子の中心複合計画を作成します。

計画の中心点の数。非負の整数、"uniform"、または "orthogonal" として指定します。center="uniform" を指定した場合、関数は精度が一様な計画に必要な中心点の数を選択します。center="orthogonal" (既定) を指定した場合、関数は直交計画に必要な中心点の数を選択します。

例: Center=3

データ型: single | double | string array

要因計画のインデックス。範囲 [0,4] の整数スカラーとして指定します。fraction の許容範囲値は、n の値に応じて変化します。たとえば、n ≤ 4 の場合、fraction に非ゼロ値を指定することはできません。fraction > 0 の場合は、完全要因キューブの (0.5)^fraction である計画が生成されます。fraction の既定値は、n に応じて変化します。

因子数fraction の既定値計画の比率
n ≤ 4 または n > 110キューブ全体
5 ≤ n ≤ 71キューブの 1/2
8 ≤ n ≤ 92キューブの 1/4
n = 103キューブの 1/8
n = 114キューブの 1/16

例: Fraction=3

データ型: single | double

ブロックあたりの最大点数。正の整数として指定します。既定値は Inf です。

例: BlockSize=3

データ型: single | double

中心複合計画のタイプ。"circumscribed"、"inscribed"、または "faced" として指定します。内接計画は外接と同じですが、すべての因子の値が因子 K=(2^(n – fraction))^(–0.25) でスケーリングされます。面接計画は外接と同じですが、スター因子の値のみが K でスケーリングされます。中心複合計画のタイプの詳細については、応答曲面計画の紹介を参照してください。

例: Type="faced"

データ型: single | double

出力引数

すべて折りたたむ

n 因子の中心複合計画。サイズが m 行 n 列の数値行列として返されます。ここで、m は計画の実行回数 (点数) です。dCC の各行には、その実行のすべての因子の設定が含まれます。因子の値は、計画のキューブ ポイントが –1 と 1 の間の値を取るように正規化されます。

実行ごとのブロック番号。m 行 1 列の数値ベクトルとして返されます。ここで、m は計画の実行回数です。ブロックは、パラメーター推定においてブロック間の差の影響を最小にするために同様の条件で測定される実行のことを指します。詳細については、[2]を参照してください。

参照

[1] Box, G. E. P., and K. B. Wilson. "On the Experimental Attainment of Optimum Conditions." Journal of the Royal Statistical Society: Series B (Methodological) 13, no. 1 (January 1951): 1–38. https://doi.org/10.1111/j.2517-6161.1951.tb00067.x.

[2] Box, G. E. P., W. G. Hunter, and J. S. Hunter. Statistics for Experimenters. Hoboken, NJ: Wiley-Interscience, 1978.

[3] Box, G. E. P., W. G. Hunter, and J. S. Hunter. "Multi-Factor Experimental Designs for Exploring Response Surfaces." Annals of Mathematical Statistics 28, no. 1 (March 1957): 195–241. https://doi.org/10.1214/aoms/1177707047.

バージョン履歴

R2006a より前に導入

参考

トピック