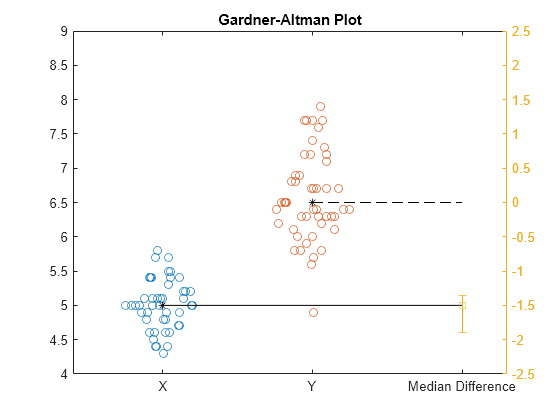
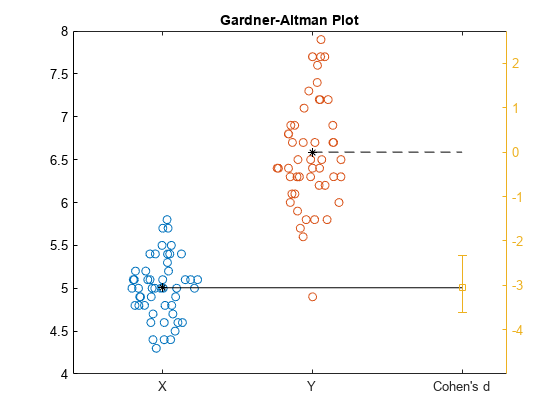
meanEffectSize
説明
例
入力引数
名前と値の引数
出力引数
アルゴリズム
参照
[1] Cousineau, Denis, and Jean-Christophe Goulet-Pelletier. "A Study of Confidence Intervals for Cohen's d in Within-Subject Designs with New Proposals." The Quantitative Methods for Psychology 17, no. 1 (March 2021): 51--75. https://doi.org/10.20982/tqmp.17.1.p051.
[2] Algina, James, H. J. Keselman, and R. D. Penfield. "An Alternative to Cohen's Standardized Mean Difference Effect Size: A Robust Parameter and Confidence Interval in the Two Independent Groups Case." Psychological Methods 10, no. 3 (Sept 2005): 317–28. https://doi.org/10.1037/1082-989X.10.3.317.
[3] Hess, Melinda, and Jeffrey Kromrey. "Robust Confidence Intervals for Effect Sizes: A Comparative Study of Cohen's d and Cliff's Delta Under Non-normality and Heterogeneous Variances." Annual Meeting of the American Educational Research Association. 2004.
[4] Delacre, Marie, Daniel Lakens, Christophe Ley, Limin Liu, and Christophe Leys. "Why Hedges G's Based on the Non-pooled Standard Deviation Should Be Reported with Welch's T-test." 2021.
[5] Gardner, M. J., and D. G. Altman. Confidence Intervals Rather Than P Values; Estimation Rather Than Hypothesis Testing." BMJ, 292 no. 6522 (March 1986): 746–50. https://doi.org/10.1136/bmj.292.6522.746.
拡張機能
バージョン履歴
R2022a で導入