fitrqnet
Syntax
Description
Mdl = fitrqnet(Tbl,ResponseVarName)Mdl. The
function trains the model using the predictors in the table Tbl and the
response values in the ResponseVarName table variable.
By default, the function uses the median (0.5 quantile).
Mdl = fitrqnet(___,Name=Value)Quantiles name-value argument.
[
also returns Mdl,AggregateOptimizationResults] = fitrqnet(___)AggregateOptimizationResults, which contains
hyperparameter optimization results when you specify the
OptimizeHyperparameters and
HyperparameterOptimizationOptions name-value arguments. You must also
specify the ConstraintType and ConstraintBounds
options of HyperparameterOptimizationOptions. You can use this syntax
to optimize on the compact model size instead of the cross-validation loss, and to solve a
set of multiple optimization problems that have the same options but different constraint
bounds. (since R2025a)
Note
Hyperparameter optimization is supported only for models with one quantile.
Examples
Fit a quantile neural network regression model using the 0.25, 0.50, and 0.75 quantiles.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a matrix X containing the predictor variables Acceleration, Displacement, Horsepower, and Weight. Store the response variable MPG in the variable Y.
load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
Y = MPG;Delete rows of X and Y where either array has missing values.
R = rmmissing([X Y]); X = R(:,1:end-1); Y = R(:,end);
Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.
rng(0,"twister") % For reproducibility of the partition c = cvpartition(length(Y),"Holdout",0.20); trainingIdx = training(c); XTrain = X(trainingIdx,:); YTrain = Y(trainingIdx); testIdx = test(c); XTest = X(testIdx,:); YTest = Y(testIdx);
Train a quantile neural network regression model. Specify to use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, standardize the numeric predictors. Use a ridge (L2) regularization term of 1. Adding a regularization term can help prevent quantile crossing.
Mdl = fitrqnet(XTrain,YTrain,Quantiles=[0.25,0.50,0.75], ...
Standardize=true,Lambda=0.05)Mdl =
RegressionQuantileNeuralNetwork
ResponseName: 'Y'
CategoricalPredictors: []
LayerSizes: 10
Activations: 'relu'
OutputLayerActivation: 'none'
Quantiles: [0.2500 0.5000 0.7500]
Properties, Methods
Mdl is a RegressionQuantileNeuralNetwork model object. You can use dot notation to access the properties of Mdl. For example, Mdl.LayerWeights and Mdl.LayerBiases contain the weights and biases, respectively, for the fully connected layers of the trained model.
In this example, you can use the layer weights, layer biases, predictor means, and predictor standard deviations directly to predict the test set responses for each of the three quantiles in Mdl.Quantiles. In general, you can use the predict object function to make quantile predictions.
firstFCStep = (Mdl.LayerWeights{1})*((XTest-Mdl.Mu)./Mdl.Sigma)' ...
+ Mdl.LayerBiases{1};
reluStep = max(firstFCStep,0);
finalFCStep = (Mdl.LayerWeights{end})*reluStep + Mdl.LayerBiases{end};
predictedY = finalFCStep'predictedY = 78×3
13.9602 15.1340 16.6884
11.2792 12.2332 13.4849
19.5525 21.7303 23.9473
22.6950 25.5260 28.1201
10.4533 11.3377 12.4984
17.6935 19.5194 21.5152
12.4312 13.4797 14.8614
11.7998 12.7963 14.1071
16.6860 18.3305 20.2070
24.1142 27.0301 29.7811
22.2832 25.1327 27.6841
12.8749 13.9594 15.3917
12.2328 13.2643 14.6245
24.0164 26.9150 29.6545
13.4641 14.5970 16.0957
⋮
isequal(predictedY,predict(Mdl,XTest))
ans = logical
1
Each column of predictedY corresponds to a separate quantile (0.25, 0.5, or 0.75).
Visualize the predictions of the quantile neural network regression model. First, create a grid of predictor values.
minX = floor(min(X))
minX = 1×4
8 68 46 1613
maxX = ceil(max(X))
maxX = 1×4
25 455 230 5140
gridX = zeros(100,size(X,2)); for p = 1:size(X,2) gridp = linspace(minX(p),maxX(p))'; gridX(:,p) = gridp; end
Next, use the trained model Mdl to predict the response values for the grid of predictor values.
gridY = predict(Mdl,gridX)
gridY = 100×3
31.2419 35.0661 38.6357
30.8637 34.6317 38.1573
30.4854 34.1972 37.6789
30.1072 33.7627 37.2005
29.7290 33.3283 36.7221
29.3507 32.8938 36.2436
28.9725 32.4593 35.7652
28.5943 32.0249 35.2868
28.2160 31.5904 34.8084
27.8378 31.1560 34.3300
27.4596 30.7215 33.8516
27.0814 30.2870 33.3732
26.7031 29.8526 32.8948
26.3249 29.4181 32.4164
25.9467 28.9837 31.9380
⋮
For each observation in gridX, the predict object function returns predictions for the quantiles in Mdl.Quantiles.
View the gridY predictions for the second predictor (Displacement). Compare the quantile predictions to the true test data values.
predictorIdx = 2; plot(XTest(:,predictorIdx),YTest,".") hold on plot(gridX(:,predictorIdx),gridY(:,1)) plot(gridX(:,predictorIdx),gridY(:,2)) plot(gridX(:,predictorIdx),gridY(:,3)) hold off xlabel("Predictor (Displacement)") ylabel("Response (MPG)") legend(["True values","0.25 predicted values", ... "0.50 predicted values","0.75 predicted values"]) title("Test Data")
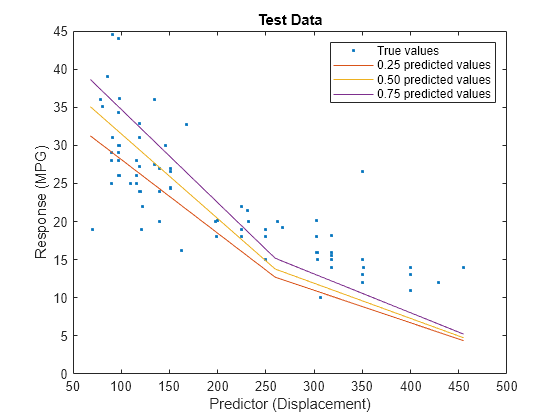
The red curve shows the predictions for the 0.25 quantile, the yellow curve shows the predictions for the 0.50 quantile, and the purple curve shows the predictions for the 0.75 quantile. The blue points indicate the true test data values.
Notice that the quantile prediction curves do not cross each other.
When training a quantile neural network regression model, you can use a ridge (L2) regularization term to prevent quantile crossing.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Cylinders, Displacement, and so on, as well as the response variable MPG.
load carbig cars = table(Acceleration,Cylinders,Displacement, ... Horsepower,Model_Year,Origin,Weight,MPG);
Remove rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition the data into training and test sets using cvpartition. Use approximately 80% of the observations as training data, and 20% of the observations as test data.
rng(0,"twister") % For reproducibility of the data partition c = cvpartition(height(cars),"Holdout",0.20); trainingIdx = training(c); carsTrain = cars(trainingIdx,:); testIdx = test(c); carsTest = cars(testIdx,:);
Train a quantile neural network regression model. Use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, standardize the numeric predictors before training.
Mdl = fitrqnet(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ... Standardize=true);
Mdl is a RegressionNeuralNetwork model object.
Determine if the test data predictions for the quantiles in Mdl.Quantiles cross each other by using the predict object function of Mdl. The crossingIndicator output argument contains a value of 1 (true) for any observation with quantile predictions that cross.
[~,crossingIndicator] = predict(Mdl,carsTest); sum(crossingIndicator)
ans = 2
In this example, two of the observations in carsTest have quantile predictions that cross each other.
To prevent quantile crossing, specify the Lambda name-value argument in the call to fitrqnet. Use a 0.05 ridge (L2) penalty term.
newMdl = fitrqnet(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ... Standardize=true,Lambda=0.05); [predictedY,newCrossingIndicator] = predict(newMdl,carsTest); sum(newCrossingIndicator)
ans = 0
With regularization, the predictions for the test data set do not cross for any observations.
Visualize the predictions returned by newMdl by using a scatter plot with a reference line. Plot the predicted values along the vertical axis and the true response values along the horizontal axis. Points on the reference line indicate correct predictions.
plot(carsTest.MPG,predictedY(:,1),".") hold on plot(carsTest.MPG,predictedY(:,2),".") plot(carsTest.MPG,predictedY(:,3),".") plot(carsTest.MPG,carsTest.MPG) hold off xlabel("True MPG") ylabel("Predicted MPG") legend(["0.25 quantile values","0.50 quantile values", ... "0.75 quantile values","Reference line"], ... Location="southeast") title("Test Data")
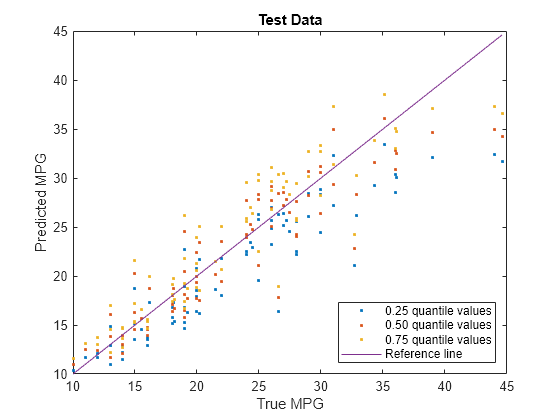
Blue points correspond to the 0.25 quantile, red points correspond to the 0.50 quantile, and yellow points correspond to the 0.75 quantile.
For a more in-depth example, see Regularize Quantile Regression Model to Prevent Quantile Crossing.
Input Arguments
Sample data used to train the model, specified as a table. Each row of Tbl
corresponds to one observation, and each column corresponds to one predictor variable.
Optionally, Tbl can contain one additional column for the response
variable. Multicolumn variables and cell arrays other than cell arrays of character
vectors are not allowed.
If
Tblcontains the response variable, and you want to use all remaining variables inTblas predictors, then specify the response variable by usingResponseVarName.If
Tblcontains the response variable, and you want to use only a subset of the remaining variables inTblas predictors, then specify a formula by usingformula.If
Tbldoes not contain the response variable, then specify a response variable by usingY. The length of the response variable and the number of rows inTblmust be equal.
Response variable name, specified as the name of a variable in
Tbl. The response variable must be a numeric vector.
You must specify ResponseVarName as a character vector or string
scalar. For example, if Tbl stores the response variable
Y as Tbl.Y, then specify it as
"Y". Otherwise, the software treats all columns of
Tbl, including Y, as predictors when
training the model.
Data Types: char | string
Explanatory model of the response variable and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y~x1+x2+x3". In this form, Y represents the
response variable, and x1, x2, and
x3 represent the predictor variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Predictor data used to train the model, specified as a numeric matrix.
By default, the software treats each row of X as one
observation, and each column as one predictor.
The length of Y and the number of observations in
X must be equal.
To specify the names of the predictors in the order of their appearance in
X, use the PredictorNames name-value
argument.
Note
If you orient your predictor matrix so that observations correspond to columns and
specify ObservationsIn="columns", then you might experience a
significant reduction in computation time.
Data Types: single | double
Note
The software treats NaN, empty character vector
(''), empty string (""),
<missing>, and <undefined> elements as
missing values, and removes observations with any of these characteristics:
Missing value in the response (for example,
YorValidationData{2})At least one missing value in a predictor observation (for example, a row in
XorValidationData{1})NaNvalue or0weight (for example, a value inWeightsorValidationData{3})
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: fitrqnet(Tbl,"MPG",Quantiles=[0.25 0.5
0.75],Standardize=true) specifies to use the 0.25, 0.5, and 0.75 quantiles and
to standardize the data before training.
Neural Network Options
Quantiles to use for training Mdl, specified as a vector of
values in the range [0,1]. The function trains a model that separates the bottom 100*q percent of training responses from the top 100*(1 – q) percent of training responses for each quantile
q.
Example: Quantiles=[0.25 0.5 0.75]
Data Types: single | double
Sizes of the fully connected layers in the quantile neural network regression
model, specified as a positive integer vector. Element i of
LayerSizes is the number of outputs in the fully connected
layer i of the neural network model.
LayerSizes does not include the size of the final fully
connected layer. For more information, see Quantile Neural Network Structure.
Example: LayerSizes=[100 25 10]
Data Types: single | double
Activation functions for the fully connected layers of the quantile neural network regression model, specified as a character vector, string scalar, string array, or cell array of character vectors with values from this table.
| Value | Description |
|---|---|
"relu" | Rectified linear unit (ReLU) function — Performs a threshold operation on each element of the input, where any value less than zero is set to zero, that is, |
"tanh" | Hyperbolic tangent (tanh) function — Applies the |
"sigmoid" | Sigmoid function — Performs the following operation on each input element: |
"none" | Identity function — Returns each input element without performing any transformation, that is, f(x) = x |
If you specify one activation function only, then
Activationsis the activation function for every fully connected layer of the neural network model, excluding the final fully connected layer (see Quantile Neural Network Structure).If you specify an array of activation functions, then element i of
Activationsis the activation function for layer i of the neural network model.
Example: Activations="sigmoid"
Data Types: char | string | cell
Function to initialize the fully connected layer weights, specified as
"glorot" or "he".
| Value | Description |
|---|---|
"glorot" | Initialize the weights with the Glorot initializer [1] (also
known as the Xavier initializer). For each layer, the Glorot initializer
independently samples from a uniform distribution with zero mean and
variance 2/(I+O), where I is the input
size and O is the output size for the layer. |
"he" | Initialize the weights with the He initializer [2]. For each
layer, the He initializer samples from a normal distribution with zero mean
and variance 2/I, where I is the input
size for the layer. |
Example: LayerWeightsInitializer="he"
Data Types: char | string
Type of initial fully connected layer biases, specified as
"zeros" or "ones".
If you specify the value
"zeros", then each fully connected layer has an initial bias of 0.If you specify the value
"ones", then each fully connected layer has an initial bias of 1.
Example: LayerBiasesInitializer="ones"
Data Types: char | string
Predictor data observation dimension, specified as "rows" or
"columns".
Note
If you orient your predictor matrix so that observations correspond to columns and
specify ObservationsIn="columns", then you might experience a
significant reduction in computation time. You cannot specify
ObservationsIn="columns" for predictor data in a
table.
Example: ObservationsIn="columns"
Data Types: char | string
Regularization term strength, specified as a nonnegative scalar. The software constructs the objective function for minimization from the quantile loss averaged over the quantiles (see Quantile Loss) and the ridge (L2) penalty term.
Example: Lambda=1e-4
Data Types: single | double
Flag to standardize the predictor data, specified as a numeric or logical
0 (false) or 1
(true). If you set Standardize to
true, then the software centers and scales each numeric predictor
variable by the corresponding column mean and standard deviation. The software does not
standardize categorical predictors.
Example:
Standardize=true
Data Types: single | double | logical
Convergence Control Options
Verbosity level, specified as 0 or 1. The
Verbose name-value argument controls the display of diagnostic
information at the command line.
| Value | Description |
|---|---|
0 | fitrqnet does not display diagnostic
information. |
1 | fitrqnet periodically displays diagnostic
information. |
fitrqnet stores the diagnostic information in
Mdl. Use Mdl.ConvergenceInfo.History to
access the diagnostic information.
Example: Verbose=1
Data Types: single | double
Frequency of verbose printing, which is the number of iterations between printing diagnostic information at the command line, specified as a positive integer scalar. A value of 1 indicates to print diagnostic information at every iteration.
Note
To use this name-value argument, you must set
Verbose to
1.
Example: VerboseFrequency=5
Data Types: single | double
Initial step size, specified as a positive scalar or "auto". By
default, fitrqnet does not use the initial step size to
determine the initial Hessian approximation used in training the model. However, if
you specify an initial step size , then the initial inverse-Hessian approximation is . is the initial gradient vector, and is the identity matrix.
To have fitrqnet determine an initial step size
automatically, specify the value as "auto". In this case, the
function determines the initial step size by using . is the initial step vector, and is the vector of unconstrained initial weights and biases.
Example: InitialStepSize="auto"
Data Types: single | double | char | string
Maximum number of training iterations, specified as a positive integer scalar.
The software returns a trained model regardless of whether the training routine
successfully converges. Mdl.ConvergenceInfo.ConvergenceCriterion
contains convergence information.
Example: IterationLimit=1e8
Data Types: single | double
Relative gradient tolerance, specified as a nonnegative scalar.
Let be the loss function at training iteration t, be the gradient of the loss function with respect to the weights and biases at iteration t, and be the gradient of the loss function at an initial point. If , where , then the training process terminates.
Example: GradientTolerance=1e-5
Data Types: single | double
Loss tolerance, specified as a nonnegative scalar.
If the function loss at some iteration is smaller than LossTolerance, then the training process terminates.
Example: LossTolerance=1e-8
Data Types: single | double
Step size tolerance, specified as a nonnegative scalar.
If the step size at some iteration is smaller than StepTolerance, then the training process terminates.
Example: StepTolerance=1e-4
Data Types: single | double
Validation data for training convergence detection, specified as a cell array or a table.
During the training process, the software periodically estimates the validation loss by using ValidationData. If the validation loss increases more than ValidationPatience times consecutively, then the software terminates the training.
You can specify ValidationData as a table if you use a table Tbl of predictor data that contains the response variable. In this case, ValidationData must contain the same predictors and response contained in Tbl. The software does not apply weights to observations, even if Tbl contains a vector of weights. To specify weights, you must specify ValidationData as a cell array.
If you specify ValidationData as a cell array, then it must have the following format:
ValidationData{1}must have the same data type and orientation as the predictor data. That is, if you use a predictor matrixX, thenValidationData{1}must be an m-by-p or p-by-m matrix of predictor data that has the same orientation asX. The predictor variables in the training dataXandValidationData{1}must correspond. Similarly, if you use a predictor tableTblof predictor data, thenValidationData{1}must be a table containing the same predictor variables contained inTbl. The number of observations inValidationData{1}and the predictor data can vary.ValidationData{2}must match the data type and format of the response variable, eitherYorResponseVarName. IfValidationData{2}is an array of responses, then it must have the same number of elements as the number of observations inValidationData{1}. IfValidationData{1}is a table, thenValidationData{2}can be the name of the response variable in the table. If you want to use the sameResponseVarNameorformula, you can specifyValidationData{2}as[].Optionally, you can specify
ValidationData{3}as an m-dimensional numeric vector of observation weights or the name of a variable in the tableValidationData{1}that contains observation weights. The software normalizes the weights with the validation data so that they sum to 1.
If you specify ValidationData and want to display the
validation loss at the command line, set Verbose to
1.
Data Types: table | cell
Number of iterations between validation evaluations, specified as a positive integer scalar. A value of 1 indicates to evaluate validation metrics at every iteration.
Note
To use this name-value argument, you must specify ValidationData.
Example: ValidationFrequency=5
Data Types: single | double
Stopping condition for validation evaluations, specified as a nonnegative integer
scalar. Training stops if the validation loss is greater than or equal to the minimum
validation loss computed so far, ValidationPatience times
consecutively. You can check the Mdl.ConvergenceInfo.History table
to see the running total of times that the validation loss is greater than or equal to
the minimum (Validation Checks).
Example: ValidationPatience=10
Data Types: single | double
Other Regression Options
Categorical predictors list, specified as one of the values in this table. The descriptions assume that the predictor data has observations in rows and predictors in columns.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the
predictor data is in a table (Tbl), fitrqnet
assumes that a variable is categorical if it is a logical vector, categorical vector, character
array, string array, or cell array of character vectors. If the predictor data is a matrix
(X), fitrqnet assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
For the identified categorical predictors, fitrqnet creates
dummy variables using two different schemes, depending on whether a categorical variable
is unordered or ordered. For an unordered categorical variable,
fitrqnet creates one dummy variable for each level of the
categorical variable. For an ordered categorical variable,
fitrqnet creates one less dummy variable than the number of
categories. For details, see Automatic Creation of Dummy Variables.
Example: CategoricalPredictors="all"
Data Types: single | double | logical | char | string | cell
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the predictor order inX. Assuming thatXhas the default orientation, with observations in rows and predictors in columns,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitrqnetuses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: PredictorNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
Response variable name, specified as a character vector or string scalar.
If you supply
Y, then you can useResponseNameto specify a name for the response variable.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: ResponseName="response"
Data Types: char | string
Function for transforming raw response values, specified as a function handle or
function name. The default is "none", which means
@(y)y, or no transformation. The function should accept a vector
(the original response values) and return a vector of the same size (the transformed
response values).
Example: Suppose you create a function handle that applies an exponential
transformation to an input vector by using myfunction = @(y)exp(y).
Then, you can specify the response transformation as
ResponseTransform=myfunction.
Data Types: char | string | function_handle
Observation weights, specified as a nonnegative numeric vector or the name of a variable in Tbl. The software weights each observation in X or Tbl with the corresponding value in Weights. The length of Weights must equal the number of observations in X or Tbl.
If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored as Tbl.W, then specify it as "W". Otherwise, the software treats all columns of Tbl, including W, as predictors when training the model.
By default, Weights is ones(n,1), where n is the number of observations in X or Tbl.
fitrqnet normalizes the weights to sum to 1.
Data Types: single | double | char | string
Cross-Validation Options
Since R2025a
Flag to train a cross-validated model, specified as "on" or
"off".
If you specify "on", then the software trains a cross-validated
model with 10 folds.
You can override this cross-validation setting using the
CVPartition, Holdout,
KFold, or Leaveout name-value argument.
You can use only one cross-validation name-value argument at a time to create a
cross-validated model.
Alternatively, cross-validate later by passing Mdl to the
crossval function.
Example: CrossVal="on"
Data Types: char | string
Since R2025a
Cross-validation partition, specified as a cvpartition object that specifies the type of cross-validation and the
indexing for the training and validation sets.
To create a cross-validated model, you can specify only one of these four
name-value arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Suppose you create a random partition for 5-fold cross-validation on 500
observations by using cvp = cvpartition(500,KFold=5). Then, you can
specify the cross-validation partition by setting
CVPartition=cvp.
Since R2025a
Fraction of the data used for holdout validation, specified as a scalar value in
the range (0,1). If you specify Holdout=p, then the software
completes these steps:
Randomly select and reserve
p*100% of the data as validation data, and train the model using the rest of the data.Store the compact trained model in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four
name-value arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Holdout=0.1
Data Types: double | single
Since R2025a
Number of folds to use in the cross-validated model, specified as a positive
integer value greater than 1. If you specify KFold=k, then the
software completes these steps:
Randomly partition the data into
ksets.For each set, reserve the set as validation data, and train the model using the other
k– 1 sets.Store the
kcompact trained models in ak-by-1 cell vector in theTrainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four
name-value arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: KFold=5
Data Types: single | double
Since R2025a
Leave-one-out cross-validation flag, specified as "on" or
"off". If you specify Leaveout="on", then for
each of the n observations (where n is the
number of observations, excluding missing observations, specified in the
NumObservations property of the model), the software completes
these steps:
Reserve the one observation as validation data, and train the model using the other n – 1 observations.
Store the n compact trained models in an n-by-1 cell vector in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four
name-value arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Leaveout="on"
Data Types: char | string
Note
You cannot use any cross-validation name-value argument together with the
OptimizeHyperparameters name-value argument. You can modify the
cross-validation for OptimizeHyperparameters only by using the
HyperparameterOptimizationOptions name-value argument.
Hyperparameter Optimization
Since R2025a
Parameters to optimize, specified as one of the following:
"none"— Do not optimize."auto"— Use["Activations","Lambda","LayerSizes","Standardize"]."all"— Optimize all eligible parameters.String array or cell array of eligible parameter names.
Vector of
optimizableVariableobjects, typically the output ofhyperparameters.
You can optimize hyperparameters only when creating a quantile regression model
with one quantile (that is, the Quantiles name-value argument has
one element).
The optimization attempts to minimize the cross-validation loss
(error) for fitrqnet by varying the parameters. To control the
cross-validation type and other aspects of the optimization, use the
HyperparameterOptimizationOptions name-value argument. When you use
HyperparameterOptimizationOptions, you can use the (compact) model size
instead of the cross-validation loss as the optimization objective by setting the
ConstraintType and ConstraintBounds options.
Note
The values of OptimizeHyperparameters override any values you
specify using other name-value arguments. For example, setting
OptimizeHyperparameters to "auto" causes
fitrqnet to optimize hyperparameters corresponding to the
"auto" option and to ignore any specified values for the
hyperparameters.
The eligible parameters for fitrqnet are:
Activations—fitrqnetoptimizesActivationsover the set["relu","tanh","sigmoid","none"].Lambda—fitrqnetoptimizesLambdaover log-scaled values in the range[1e-5/NumObservations,1e5/NumObservations].LayerBiasesInitializer—fitrqnetoptimizesLayerBiasesInitializerover the two values["zeros","ones"].LayerWeightsInitializer—fitrqnetoptimizesLayerWeightsInitializerover the two values["glorot","he"].LayerSizes—fitrqnetoptimizes over the values1,2, and3representing the number of fully connected layers, excluding the final fully connected layer.fitrqnetoptimizes each fully connected layer separately over1through300sizes in the layer, sampled on a logarithmic scale.Note
When you use the
LayerSizesargument, the iterative display shows the size of each relevant layer. For example, if the current number of fully connected layers is3, and the three layers are of size10,79, and44(respectively), the iterative display showsLayerSizesfor that iteration as[10 79 44].Note
To access up to five fully connected layers or a different range of sizes in a layer, use
hyperparametersto select the optimizable parameters and ranges.Standardize—fitrqnetoptimizesStandardizeover the two values[true,false].
Set nondefault parameters by passing a vector of
optimizableVariable objects that have nondefault values. For
example, this code sets the range of NumLayers to [1
5] and optimizes Layer_4_Size and
Layer_5_Size:
load carsmall params = hyperparameters("fitrqnet",[Horsepower,Weight],MPG); params(1).Range = [1 5]; params(10).Optimize = true; params(11).Optimize = true;
Pass params as the value of
OptimizeHyperparameters.
By default, the iterative display appears at the command line,
and plots appear according to the number of hyperparameters in the optimization. For the
optimization and plots, the objective function is log(1 + cross-validation loss). To control the iterative display, set the Verbose option
of the HyperparameterOptimizationOptions name-value argument. To control
the plots, set the ShowPlots option of the
HyperparameterOptimizationOptions name-value argument.
Example: OptimizeHyperparameters="auto"
Since R2025a
Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument
modifies the effect of the OptimizeHyperparameters name-value
argument. If you specify HyperparameterOptimizationOptions, you
must also specify OptimizeHyperparameters. All the options listed
in the following table are optional. However, you must set
ConstraintBounds and ConstraintType to return
AggregateOptimizationResults. The options that you can set in a
structure are the same as those in the
HyperparameterOptimizationOptions object.
| Option | Values | Default |
|---|---|---|
Optimizer |
| "bayesopt" |
ConstraintBounds | Constraint bounds for N optimization problems,
specified as an N-by-2 numeric matrix or
| [] |
ConstraintTarget | Constraint target for the optimization problems, specified as
| If you specify ConstraintBounds and
ConstraintType, then the default value is
"matlab". Otherwise, the default value is
[]. |
ConstraintType | Constraint type for the optimization problems, specified as
| [] |
AcquisitionFunctionName | Type of acquisition function:
Acquisition functions whose names include
| "expected-improvement-per-second-plus" |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. If you specify multiple
optimization problems using ConstraintBounds, the value of
MaxObjectiveEvaluations applies to each optimization
problem individually. | 30 for "bayesopt" and
"randomsearch", and the entire grid for
"gridsearch" |
MaxTime | Time limit for the optimization, specified as a nonnegative real
scalar. The time limit is in seconds, as measured by | Inf |
NumGridDivisions | For Optimizer="gridsearch", the number of values in each
dimension. The value can be a vector of positive integers giving the number of
values for each dimension, or a scalar that applies to all dimensions. The
software ignores this option for categorical variables. | 10 |
ShowPlots | Logical value indicating whether to show plots of the optimization progress.
If this option is true, the software plots the best observed
objective function value against the iteration number. If you use Bayesian
optimization (Optimizer="bayesopt"), the
software also plots the best estimated objective function value. The best
observed objective function values and best estimated objective function values
correspond to the values in the BestSoFar (observed) and
BestSoFar (estim.) columns of the iterative display,
respectively. You can find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of
Mdl.HyperparameterOptimizationResults. If the problem
includes one or two optimization parameters for Bayesian optimization, then
ShowPlots also plots a model of the objective function
against the parameters. | true |
SaveIntermediateResults | Logical value indicating whether to save the optimization results. If this
option is true, the software overwrites a workspace variable
named "BayesoptResults" at each iteration. The variable is a
BayesianOptimization object. If you
specify multiple optimization problems using
ConstraintBounds, the workspace variable is an AggregateBayesianOptimization object named
"AggregateBayesoptResults". | false |
Verbose | Display level at the command line:
For details, see the | 1 |
UseParallel | Logical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization. | false |
Repartition | Logical value indicating whether to repartition the cross-validation at
every iteration. If this option is A value of
| false |
| Specify only one of the following three options. | ||
CVPartition | cvpartition object created by cvpartition | KFold=5 if you do not specify a
cross-validation option |
Holdout | Scalar in the range (0,1) representing the holdout
fraction | |
KFold | Integer greater than 1 | |
Example: HyperparameterOptimizationOptions=struct(UseParallel=true)
Output Arguments
Trained quantile neural network model, returned as a RegressionQuantileNeuralNetwork object, a RegressionPartitionedQuantileModel object, or a cell array of model objects.
If you set any of the name-value arguments
CrossVal,CVPartition,Holdout,KFold, orLeaveout, thenMdlis aRegressionPartitionedQuantileModelobject.If you specify
OptimizeHyperparametersand set theConstraintTypeandConstraintBoundsoptions ofHyperparameterOptimizationOptions, thenMdlis an N-by-1 cell array of model objects, where N is equal to the number of rows inConstraintBounds. If none of the optimization problems yields a feasible model, then each cell array value is[].Otherwise,
Mdlis aRegressionQuantileNeuralNetworkmodel object.
To reference properties of a model object, use dot notation.
Since R2025a
Aggregate optimization results for multiple optimization problems, returned as an
AggregateBayesianOptimization object. To return
AggregateOptimizationResults, you must specify
OptimizeHyperparameters and
HyperparameterOptimizationOptions. You must also specify the
ConstraintType and ConstraintBounds options
of HyperparameterOptimizationOptions. For an example that shows how
to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.
More About
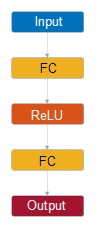
The default quantile neural network regression model has the following layer structure.
| Structure | Description |
|---|---|
|
| Input — This layer corresponds to the predictor data in
Tbl or X. |
First fully connected layer — This layer has 10 outputs, by default.
| |
ReLU activation function —
| |
Final fully connected layer — This layer has one output for each quantile
specified by the
| |
| Output — This layer corresponds to the predicted response values. |
Tips
You can use the α/2 and 1 – α/2 quantiles to create a prediction interval that captures an estimated 100*(1 – α) percent of the variation in the response. For an example, see Create Prediction Interval Using Quantiles.
You can use quantile regression models to fit models that are robust to outliers. For an example, see Fit Regression Models to Data with Outliers.
Algorithms
fitrqnet uses a limited-memory Broyden-Fletcher-Goldfarb-Shanno
quasi-Newton algorithm (LBFGS) [3] as its loss function
minimization technique, where the software minimizes the quantile loss averaged over the
quantiles (see Quantile Loss). The LBFGS solver uses a
standard line-search method with an approximation to the Hessian.
Extended Capabilities
To perform parallel hyperparameter optimization, use the UseParallel=true
option in the HyperparameterOptimizationOptions name-value argument in
the call to the fitrqnet function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2024bYou can optimize or cross-validate quantile regression models created using
fitrqnet.
To optimize the hyperparameters of a quantile regression model, specify the
OptimizeHyperparametersname-value argument.To cross-validate a quantile regression model, specify one of these name-value arguments:
CrossVal,CVPartition,Holdout,KFold, orLeaveout. Alternatively, create a full quantile regression model and then use thecrossvalobject function.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)