混合ガウス仮定の確認

判別分析では、データは混合ガウスモデルに従っています (判別分析モデルの作成を参照)。データが混合ガウスモデルに従っていると思われる場合、判別分析が適切な分類器になると予測できます。さらに、既定の線形判別分析では、すべてのクラスの共分散行列が等しいと仮定しています。ここでは、これらの仮定を確認する方法を説明します。

線形判別分析の等しい共分散行列のバートレット検定
Q-Q プロット
多変量正規性の Mardia 尖度検定

線形判別分析の等しい共分散行列のバートレット検定

バートレット検定 ([1]のボックス参照) では、さまざまなクラスの共分散行列の等価性を確認します。共分散行列が等しい場合、検定では線形判別分析が適切であると表示されます。等しくない場合、fitcdiscr で名前と値のペアの引数 DiscrimType を 'quadratic' に設定して、2 次判別分析を使用することを検討します。

バートレット検定では、平均行列も共分散行列もわかっていない標準 (ガウス) 標本を想定します。共分散が等しいかどうかを調べるために、以下の数量を計算します。

クラスあたりの標本共分散行列 Σ_i, 1 ≤ i ≤ k (k はクラスの個数)。
プールされた共分散行列 Σ。
統計 V をテストします。
$V = (n - k) \log (| Σ |) - \sum_{i = 1}^{k} (n_{i} - 1) \log (| Σ_{i} |)$
ここで、n は観測値の合計数、n_i はクラス i の観測値の数で、|Σ| は行列 Σ の行列式です。
各クラス内の観測値の個数 n_i が増えるにつれて、V は自由度が kd(d + 1)/2 の χ² 分布に漸近的に近づきます。ここで、d は予測子の個数 (データ内の次元数) です。

バートレット検定では、自由度が kd(d + 1)/2 である χ² 分布の所定の百分位数を V が超えるかどうかを確認します。超える場合、共分散が等しいという仮説を棄却します。

等しい共分散行列のバートレット検定

ライブスクリプトを開く

フィッシャーのアヤメのデータを、単一のガウス共分散でモデル化するのが適切か、あるいは等しい共分散行列のバートレット検定を実行して混合ガウスとしてモデル化するのがより適切かを確認します。

fisheriris データセットを読み込みます。

load fisheriris;
prednames = {'SepalLength','SepalWidth','PetalLength','PetalWidth'};

すべてのクラスの共分散行列が等しい場合、線形判別分析が適切です。

フィッシャーのアヤメのデータを使用して、線形判別分析モデル (既定のタイプ) に学習させます。

L = fitcdiscr(meas,species,'PredictorNames',prednames);

クラスの共分散行列が等しくない場合、2 次判別分析が適切です。

フィッシャーのアヤメのデータを使用して、2 次判別分析モデルに学習させ、統計量を計算します。

Q = fitcdiscr(meas,species,'PredictorNames',prednames,'DiscrimType','quadratic');

観測数 N、データセットの次元 D、クラス数 K、および各クラス内の観測値の個数 Nclass を変数として保存します。

[N,D] = size(meas)

N = 150

D = 4

K = numel(unique(species))

K = 3

Nclass = grpstats(meas(:,1),species,'numel')'

Nclass = 1×3

    50    50    50

検定統計量 V を計算します。

SigmaL = L.Sigma;
SigmaQ = Q.Sigma;
V = (N-K)*log(det(SigmaL));
for k=1:K
    V = V - (Nclass(k)-1)*log(det(SigmaQ(:,:,k)));
end
V

V = 146.6632

p 値を計算します。

nu = K*D*(D+1)/2;
pval1 = chi2cdf(V,nu,'upper')

pval1 = 2.6091e-17

pval1 が 0.05 より小さいため、バートレット検定により、共分散行列が等しいという仮説が棄却されます。その結果、線形判別分析ではなく、2 次判別分析を使用します。

Q-Q プロット

Q-Q プロットは、経験的分布が理論的分布に近いかどうかを図で示します。両者が等しい場合、Q-Q プロットは 45° の線上にあります。等しくない場合、Q-Q プロットは 45° の線から外れます。

線形および 2 次判別用 Q-Q プロットの比較

ライブスクリプトを開く

Q-Q プロットを解析して、フィッシャーのアヤメのデータを単一のガウス共分散でモデル化するのと混合ガウスとしてモデル化するのと、どちらがより適切かを確認します。

fisheriris データセットを読み込みます。

load fisheriris;
prednames = {'SepalLength','SepalWidth','PetalLength','PetalWidth'};

すべてのクラスの共分散行列が等しい場合、線形判別分析が適切です。

線形判別分析モデルに学習させます。

L = fitcdiscr(meas,species,'PredictorNames',prednames);

クラスの共分散行列が等しくない場合、2 次判別分析が適切です。

フィッシャーのアヤメのデータを使用して、2 次判別分析モデルに学習させます。

Q = fitcdiscr(meas,species,'PredictorNames',prednames,'DiscrimType','quadratic');

観測値の数、データセットの次元、および予測された分位数を計算します。

[N,D] = size(meas);
expQuant = chi2inv(((1:N)-0.5)/N,D);

線形判別モデルの観測された分位数を計算します。

obsL = mahal(L,L.X,'ClassLabels',L.Y);
[obsL,sortedL] = sort(obsL);

線形判別の Q-Q プロットをグラフにします。

figure;
gscatter(expQuant,obsL,L.Y(sortedL),'bgr',[],[],'off');
legend('virginica','versicolor','setosa','Location','NW');
xlabel('Expected quantile');
ylabel('Observed quantile for LDA');
line([0 20],[0 20],'color','k');

Figure contains an axes object. The axes object with xlabel Expected quantile, ylabel Observed quantile for LDA contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent virginica, versicolor, setosa.

予測された分位数と観測された分位数はある程度一致しています。プロットが 45°の線から上へ偏っている場合、データが正規分布よりも裾が重くなっていることを示します。プロットは、上部の 3 つの点が外れ値の可能性があることを示しています。クラス 'setosa' の 2 つの観測値とクラス 'virginica' の 1 つの観測値です。

2 次判別モデルの観測された分位数を計算します。

obsQ = mahal(Q,Q.X,'ClassLabels',Q.Y);
[obsQ,sortedQ] = sort(obsQ);

2 次判別の Q-Q プロットをグラフにします。

figure;
gscatter(expQuant,obsQ,Q.Y(sortedQ),'bgr',[],[],'off');
legend('virginica','versicolor','setosa','Location','NW');
xlabel('Expected quantile');
ylabel('Observed quantile for QDA');
line([0 20],[0 20],'color','k');

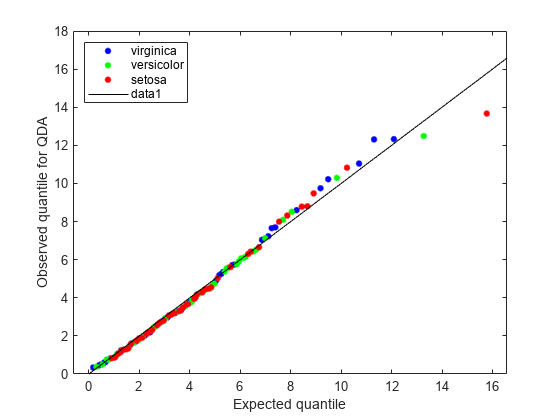
Figure contains an axes object. The axes object with xlabel Expected quantile, ylabel Observed quantile for QDA contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent virginica, versicolor, setosa.

2 次判別の Q-Q プロットは、観測された分位数と予測された分位数との間により適切な一致を示します。プロットは、クラス 'setosa' の 1 つだけが外れ値の可能性があることを示しています。フィッシャーのアヤメのデータは、クラス間での等価性を必要としない共分散行列をもつ混合ガウスとしてモデル化されるのが適切です。

多変量正規性の Mardia 尖度検定

Mardia 尖度検定 (Mardia [2] を参照) は、Q-Q プロットの検証の代わりになります。この検定は、データが混合ガウスモデルと一致するかどうかを判別するための数値的なアプローチです。

Mardia 尖度検定では、クラス平均からデータまでのマハラノビス距離の 4 乗の平均である M を計算します。一定の共分散行列をもつ正規分布にデータが従っており、線形判別分析に適している場合、M は平均が d(d + 2) で分散が 8d(d + 2)/n の正規分布に漸近的に近づきます。ここで

d は予測子の数 (データ内の次元の数) です。
n は、観測の合計数です。

Mardia 検定は両側検定であり、分散が 8d(d + 2)/n である正規分布に関して、M が d(d + 2) に十分に近いかどうかを確認します。

線形判別と 2 次判別の Mardia 尖度検定

ライブスクリプトを開く

Mardia 尖度検定を実行して、フィッシャーのアヤメのデータが線形判別分析と 2 次判別分析の両方でほぼ正規分布しているかどうかを確認します。

fisheriris データセットを読み込みます。

load fisheriris;
prednames = {'SepalLength','SepalWidth','PetalLength','PetalWidth'};

すべてのクラスの共分散行列が等しい場合、線形判別分析が適切です。

線形判別分析モデルに学習させます。

L = fitcdiscr(meas,species,'PredictorNames',prednames);

クラスの共分散行列が等しくない場合、2 次判別分析が適切です。

フィッシャーのアヤメのデータを使用して、2 次判別分析モデルに学習させます。

Q = fitcdiscr(meas,species,'PredictorNames',prednames,'DiscrimType','quadratic');

漸近分布の平均と分散を計算します。

[N,D] = size(meas);
meanKurt = D*(D+2)

meanKurt = 24

varKurt = 8*D*(D+2)/N

varKurt = 1.2800

線形判別モデルに対する Mardia 尖度検定の p 値を計算します。

mahL = mahal(L,L.X,'ClassLabels',L.Y);
meanL = mean(mahL.^2);
[~,pvalL] = ztest(meanL,meanKurt,sqrt(varKurt))

pvalL = 0.0208

pvalL が 0.05 より小さいため、Mardia 尖度検定により、データが一定の共分散行列で正規分布しているという仮説が棄却されます。

2 次判別モデルに対する Mardia 尖度検定の p 値を計算します。

mahQ = mahal(Q,Q.X,'ClassLabels',Q.Y);
meanQ = mean(mahQ.^2);
[~,pvalQ] = ztest(meanQ,meanKurt,sqrt(varKurt))

pvalQ = 0.7230

pvalQ が 0.05 より大きいため、データは多変量正規分布と整合性があります。

その結果、線形判別分析ではなく、2 次判別分析を使用します。

参照

[1] Box, G. E. P. “A General Distribution Theory for a Class of Likelihood Criteria.” Biometrika 36, no. 3–4 (1949): 317–46. https://doi.org/10.1093/biomet/36.3-4.317.

[2] Mardia, K. V. “Measures of Multivariate Skewness and Kurtosis with Applications.” Biometrika 57, no. 3 (1970): 519–30. https://doi.org/10.1093/biomet/57.3.519.