混合ガウス モデルの作成

この例では、gmdistributionを使用して成分の平均、共分散および混合比率を指定することにより、既知の、つまり完全に指定された混合ガウス モデル (GMM) オブジェクトを作成する方法を示します。データを GMM に当てはめることにより GMM オブジェクトを作成する方法については、データへの混合ガウス モデルの当てはめを参照してください。

二変量ガウス分布の 2 つの成分の混合について、成分の平均、共分散および混合比率を指定します。

mu = [1 2;-3 -5];                    % Means
sigma = cat(3,[2 0;0 .5],[1 0;0 1]); % Covariances
p = ones(1,2)/2;                     % Mixing proportions

mu の行は、成分の平均ベクトルに対応します。sigma のページ sigma(:,;,J) は、成分の共分散行列に対応します。

gmdistribution を使用して GMM オブジェクトを作成します。

gm = gmdistribution(mu,sigma,p);

GMM のプロパティを表示します。

properties(gm)

Properties for class gmdistribution:

    NumVariables
    DistributionName
    NumComponents
    ComponentProportion
    SharedCovariance
    NumIterations
    RegularizationValue
    NegativeLogLikelihood
    CovarianceType
    mu
    Sigma
    AIC
    BIC
    Converged
    ProbabilityTolerance

プロパティについては、gmdistributionを参照してください。プロパティの値にアクセスするには、ドット表記を使用します。たとえば、各 GMM 成分の変数の個数にアクセスします。

dimension = gm.NumVariables

dimension = 2

pdf と MATLAB® 関数 fsurf を使用して、GMM の確率密度関数 (pdf) を可視化します。

gmPDF = @(x,y) arrayfun(@(x0,y0) pdf(gm,[x0 y0]),x,y);
fsurf(gmPDF,[-10 10])
title('Probability Density Function of GMM');

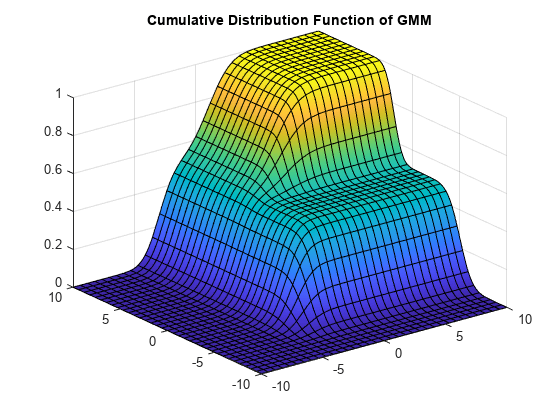
cdfと fsurf を使用して、GMM の累積分布関数 (cdf) を可視化します。

gmCDF = @(x,y) arrayfun(@(x0,y0) cdf(gm,[x0 y0]),x,y);
fsurf(gmCDF,[-10 10])
title('Cumulative Distribution Function of GMM');

参考

fitgmdist | gmdistribution

関連するトピック

• データへの混合ガウス モデルの当てはめ
• 混合ガウス モデルから派生するデータのシミュレート
• 混合ガウス モデルを使用したクラスタリング