コックス比例ハザード モデル オブジェクト
この例では、CoxModel オブジェクトを使用してコックス比例ハザード モデルの当てはめと解析を行う方法を示します。コックス比例ハザード モデルは、寿命や故障時間のデータに関連するモデルです。背景については、生存時間分析とはおよびコックス比例ハザード モデルを参照してください。
予測子と階層化レベル
コックス比例ハザード モデルの主要な仮定は、ハザード率 (瞬間故障率または事象率を意味する) がすべての時間 において基本レート に比例するというものです。比例定数は予測子 (一部の文献では共変量と呼ばれる) の値に依存します。係数 が関連付けられた予測子 のハザード率は次のようになります。
.
この例では、3 つの階層化レベルにコックス比例ハザード モデルの拡張を使用します。コックス比例ハザード モデルの拡張を参照してください。層化コックス モデルには固定数の基本レート があり、すべての階層化レベルに同じ予測子と係数が使用されます。
比例ハザードの仮定は、予測子が時間に依存しないことを意味します。時間に依存するデータをモデルに含めることもできます。比例ハザードの仮定を維持しながらこれを行うには、階層化モデルを作成します。カテゴリ化可能なデータの場合は、データのレベルごとに階層化を 1 つ作成します。これにより、それぞれの階層化で異なる基本レートが使用されます。基本レートが時間によって変わるため、比例ハザードの仮定が維持されます。時間に依存するデータの値を階層化の値として与えると、学習済みモデルから異なるハザード率が出力されます。
当てはめ用のデータの作成
次のタイプのハザード率をもつ 3 つの寿命のモデル用のデータを生成します。これらのモデルは 3 つの階層化レベルに対応します。
バスタブ (故障率が最初は高く、低いレベルまで低下した後、一定のレベルまで上昇)
対数的に増加:
で一定
3 つのモデルは、基準ハザード率について 3 つの乗算器をもつ 1 つの予測子を共有します。
11/201/100
データには、各階層化レベルと各予測子レベルから 1 つずつの組み合わせで、合計 9 種類の母集団メンバーがあります。バスタブと対数のハザード率を作成する関数については、この例の終わりにある補助関数のセクションで示しています。
予測子の値が 1 の場合の 3 つのハザード率をプロットします。
t = linspace(1,40); plot(t,hazard(t),t,log(t)/10,t,1/4*ones(size(t))) legend('Hazard 1','Hazard 2','Hazard 3','Location','northeast') ylim([0 1]) xlabel("Time") ylabel("Hazard Rate")
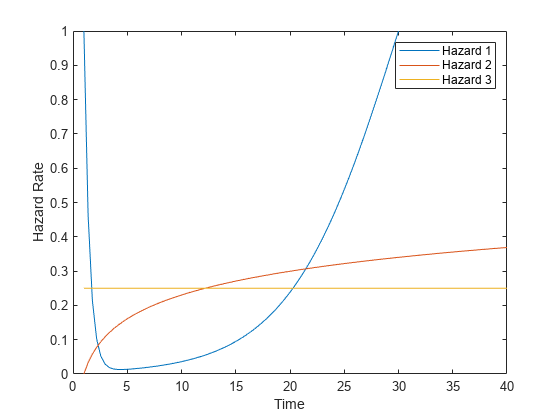
9 つのモデルに関連付けられる寿命の疑似乱数データを作成します。累積分布を反転して、無作為に選択される 9000 の標本 (各タイプ約 1000) を作成します (詳細については、Inverse transform sampling を参照)。
N = 9000; rng default % For reproducibility mults = [1;1/20;1/100]; % Three predictors strata = randi(3,N,1); % Three strata t1 = zeros(N,1); a0 = randi(3,N,1); % Predictor a1 = mults(a0); v1 = rand(N,1); for i = 1:N switch strata(i) case 1 % Bathtub t1(i) = zeropt(a1(i),v1(i)); case 2 % Logarithmic t1(i) = zeroptold(a1(i),v1(i)); case 3 % Constant t1(i) = 1 + exprnd(4/a1(i)); end end
データを table に読み込みます。
a3 = categorical(a1); tbldata = table(t1,a3,strata,'VariableNames',["Lifetime" "Predictors" "Strata"]);
コックス モデルの当てはめ
層化コックス比例ハザード モデルを table データに当てはめます。
coxMdl = fitcox(tbldata,'Lifetime ~ Predictors',"Stratification",'Strata');
生存時間のプロット
予測子の値 pred = 1 (またはこの例の実行時に任意の値を指定) と 3 つの階層化レベルについて、生存の確率を時間の関数としてプロットします。
pred =  1;
cpred = categorical(pred);
plotSurvival(coxMdl,[cpred;cpred;cpred],[1;2;3])
xlim([1,10/pred + 20])
1;
cpred = categorical(pred);
plotSurvival(coxMdl,[cpred;cpred;cpred],[1;2;3])
xlim([1,10/pred + 20])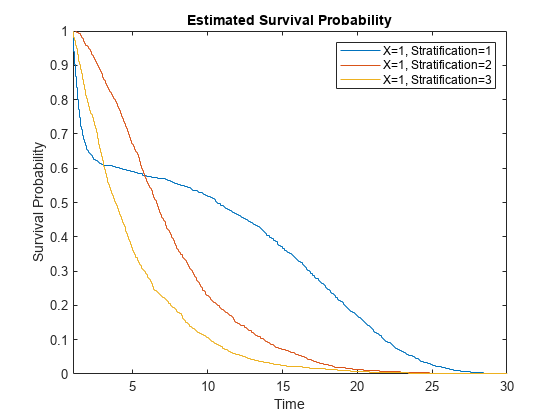
それぞれの予測子についてハザード率は比例していますが、基になるハザード関数が異なるため 3 つの生存のプロットは比例していません。
当てはめの解析
当てはめたモデルの係数を調べます。
disp(coxMdl.Coefficients)
Beta SE zStat pValue
______ ________ ______ ______
Predictors_0.05 1.5301 0.031783 48.143 0
Predictors_1 4.5593 0.052149 87.427 0
pValue のエントリが 0 になっていることに注意してください。これは、リストされた予測子の Beta の値が 0 でないことを意味します。
モデルの係数の有意水準 0.01 における信頼区間を表示します。
coefci(coxMdl,0.01)
ans = 2×2
1.4483 1.6120
4.4249 4.6936
水準 0.01 の予測子のハザードを推定するために、コックス モデルの定義を思い出してください。
.
関数 fitcox は、ダミー変数と参照グループを使用してカテゴリカル データを扱います。このケースでは、水準 0.01 の予測子が参照グループとして扱われ、モデルの当てはめにおいてすべて 0 として符号化されます。ハザード関数にすべての 0 を入力すると次のようになります。
はベースライン ハザードで、coxMdl.Hazard に格納されています。したがって、水準 0.01 の予測子のハザードを取得するには coxMdl.Hazard を調べればよいことがわかります。3 つの階層化レベルのベースライン累積ハザードをプロットします。
figure hold on for i = 1:3 pred3 = find(coxMdl.Hazard(:,3) == i); % Find indices of stratification i plot(coxMdl.Hazard(pred3,1),coxMdl.Hazard(pred3,2)) end xlabel('Time') ylabel('Cumulative Hazard') xlim([1 300]) legend('X = 0.01, Stratification 1',... 'X = 0.01, Stratification 2',... 'X = 0.01, Stratification 3','Location','northwest') hold off

他の予測子の値の累積ハザードは、ベースライン累積ハザードの 倍になります。 は推定された係数です。
disp(exp(coxMdl.Coefficients.Beta))
4.6188 95.5127
これらの相対ハザードの値は、乗算器 1、1/20、および 1/100 で生成されたデータの理論値に近い値になります。ベースライン値は 1/100 の乗算器に対応するため、理論上の乗算器は 5 と 100 です。
linhyptest のテーブルを表示します。
linhyptest(coxMdl)
ans=2×2 table
Predictor pValue
___________________ ______
{'Empty Model' } 0
{'Predictors_0.05'} 0
ここでも、値 1/20 の予測子と値 1 の予測子がモデルに必要になります。
このデータがコックス比例ハザード モデルによるデータであるという仮説を支持するデータであるかどうかを確認します。
supports = coxMdl.ProportionalHazardsPValueGlobal
supports = 0.9730
この検定の帰無仮説は、このデータがコックス比例ハザード モデルによるデータであるということです。この仮説を棄却するには、supports の有意水準が 0.05 未満のような小さい値でなければなりません。この統計は、データがコックス モデルと一致するという仮説がサポートされることを示します。
ハザード率の確認
3 つの階層化レベルについて、予測子の値 1、1/20、および 1/100 のベースライン 0 に対するハザード率を計算します。
hazards = hazardratio(coxMdl,... categorical([1;1;1;1/20;1/20;1/20;1/100;1/100;1/100]),... [1;2;3;1;2;3;1;2;3],'Baseline',0)
hazards = 9×1
95.5127
95.5127
95.5127
4.6188
4.6188
4.6188
1.0000
1.0000
1.0000
ハザード率は、前のセクションで説明したとおり、理論値の 100、5、および 1 に近い値になっています。ハザード率は階層化レベルには依存していません。
ハザードが一定の階層化レベルが理論とどの程度一致するかの検証
階層化レベル 3 のハザード率は 1/4 で一定です。理論的には、一定なハザード率は、対数が直線である指数生存時間関数を意味します。予測子の値 1/20 を使用してレベル 3 の階層化の生存時間をプロットします。指数の率は 1/80 になります。
tt = categorical(1/20); h = figure; axes1 = axes('Parent',h); plotSurvival(coxMdl,axes1,tt,3); xlim([1 400]); axes1.YScale = 'log'; hold on tms = linspace(1,400); semilogy(tms,exp(-tms/80),'r--') hold off
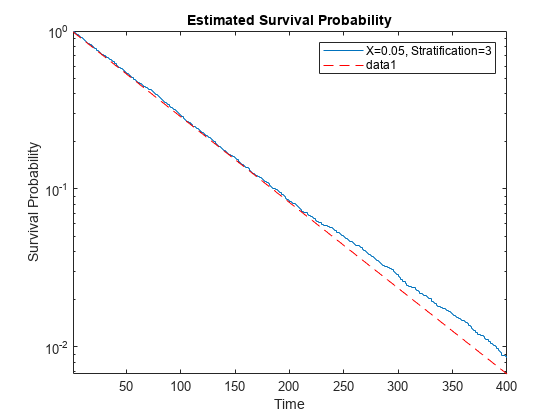
データは、1/100 を大きく上回る確率で、理論上のラインに一致します。
残差の破棄によるメモリ使用量の削減
モデルで使用されるメモリを調べます。
M1 = whos("coxMdl");
disp(M1.bytes)1231741
モデルから残差を削除します。
coxMdl = discardResiduals(coxMdl);
モデルで使用されるメモリに対する削除による影響を調べます。
M2 = whos("coxMdl");
disp(M2.bytes)438173
disp(M1.bytes/M2.bytes)
2.8111
残差を削除することで、メモリ使用量がほぼ 3 分の 1 に減少しています。
補助関数
この関数は、バスタブのハザード率を作成します。
function h = hazard(x) h = exp(-2*(x - 1)) + (1 + tanh(x/10 - 3)); end
この関数は、バスタブのハザード率の 1 から x までの積分を作成します。
function eh = exphazard(x) eh = 1/2 - exp(-2*(x-1))/2; eh2 = (10*log(cosh(x/10 - 3)) - 10*log(cosh(1/10 - 3)) + x - 1); eh = eh + eh2; end
この関数は、乗算器 a を使用して累積ハザード率のレベル v までの平方根を求めます。
function zz = zeropt(a,v) zz = fzero(@(x)(1 - exp(-a*exphazard(x)) - v),[1 100*max(1,1/a)]); end
この関数は、乗算器 1/10 を使用して対数のハザード率の 1 から x までの積分を作成します。
function cr = cumrisk(x) cr = 1/10*(x.*(log(x) - 1) + 1); end
この関数は、乗算器 a を使用して累積ハザード率のレベル v までの平方根を求めます。
function zz = zeroptold(a,v) zz = fzero(@(x)(1 - exp(-a*cumrisk(x)) - v),[1 50*max(1,1/a)]); end